R'de tukey testi nasıl yapılır?

Üç veya daha fazla bağımsız grubun ortalamaları arasında istatistiksel olarak anlamlı bir fark olup olmadığını belirlemek için tek yönlü ANOVA kullanılır.

ANOVA tablosunun genel p değeri belirli bir anlamlılık düzeyinin altındaysa, grup ortalamalarından en az birinin diğerlerinden farklı olduğunu söylemek için yeterli kanıtımız var demektir.

Ancak bu bize hangi grupların birbirinden farklı olduğunu söylemez. Bu bize basitçe tüm grup ortalamalarının eşit olmadığını söyler. Hangi grupların birbirinden farklı olduğunu tam olarak bilmek için post hoc test yapmamız gerekir.

En sık kullanılan post hoc testlerden biri, aile bazında hata oranını kontrol ederken her grubun ortalamaları arasında ikili karşılaştırmalar yapmamıza olanak tanıyan Tukey testidir .

Bu eğitimde R’de Tukey testinin nasıl gerçekleştirileceği açıklanmaktadır.

Not: Çalışmanızdaki gruplardan herhangi biri kontrol grubu olarak kabul ediliyorsa bunun yerine post-hoc test olarak Dunnett testini kullanmalısınız.

Örnek: R’de Tukey testi

Adım 1: ANOVA modelini yerleştirin.

Aşağıdaki kod, üç grupla (A, B ve C) sahte bir veri kümesinin nasıl oluşturulacağını ve her grubun ortalama değerlerinin eşit olup olmadığını belirlemek için verilere tek yönlü bir ANOVA modelinin nasıl yerleştirileceğini gösterir:

 #make this example reproducible
set.seed(0)

#create data
data <- data.frame(group = rep (c("A", "B", "C"), each = 30),
                   values = c(runif(30, 0, 3),
                                   runif(30, 0, 5),
                                   runif(30, 1, 7)))

#view first six rows of data
head(data)

  group values
1 A 2.6900916
2 A 0.7965260
3 A 1.1163717
4 A 1.7185601
5 A 2.7246234
6 A 0.6050458

#fit one-way ANOVA model
model <- aov (values~group, data=data)

#view the model output
summary(model)

            Df Sum Sq Mean Sq F value Pr(>F)    
group 2 98.93 49.46 30.83 7.55e-11 ***
Residuals 87 139.57 1.60                     
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

ANOVA tablosundan genel p değerinin 7,55e-11 olduğunu görebiliriz. Bu sayı 0,05’ten küçük olduğundan her gruptaki ortalama değerlerin eşit olmadığını söyleyebilecek yeterli kanıtımız var. Yani tam olarak hangi grup ortalamalarının farklı olduğunu belirlemek için Tukey testini yapabiliriz.

Adım 2: Tukey testini gerçekleştirin.

Aşağıdaki kod, Tukey testini gerçekleştirmek için TukeyHSD() işlevinin nasıl kullanılacağını gösterir:

 #perform Tukey's Test
TukeyHSD(model, conf.level= .95 ) 

  Tukey multiple comparisons of means
    95% family-wise confidence level

Fit: aov(formula = values ~ group, data = data)

$group
         diff lwr upr p adj
BA 0.9777414 0.1979466 1.757536 0.0100545
CA 2.5454024 1.7656076 3.325197 0.0000000
CB 1.5676610 0.7878662 2.347456 0.0000199

P değeri, her program arasında istatistiksel olarak anlamlı bir fark olup olmadığını gösterir. Sonuçlar, her programın ortalama kilo kaybı arasında 0,05 anlamlılık düzeyinde istatistiksel olarak anlamlı bir fark olduğunu göstermektedir.

Özellikle:

• B ve A arasındaki ortalama fark için P değeri: 0,0100545
• C ve A arasındaki ortalama fark için P değeri: 0,0000000
• C ve B arasındaki ortalama fark için P değeri: 0,0000199

Adım 3: Sonuçları görselleştirin.

Güven aralıklarını görselleştirmek için arsa(TukeyHSD()) fonksiyonunu da kullanabiliriz:

 #plot confidence intervals
plot(TukeyHSD(model, conf.level= .95 ), las = 2 )

Not: las argümanı, onay etiketlerinin eksene dik (las=2) olması gerektiğini belirtir.

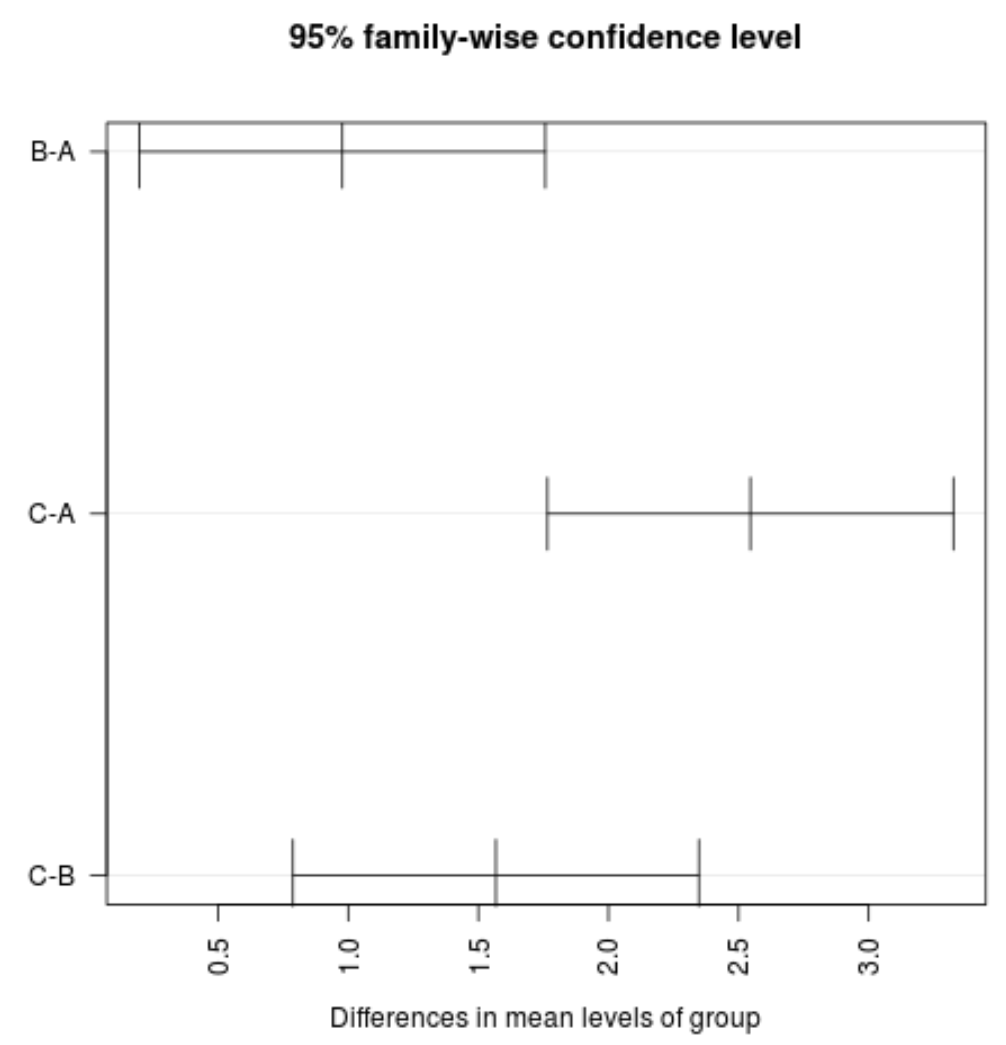
Gruplar arasındaki ortalama değere ilişkin güven aralıklarının hiçbirinin sıfır değerini içermediğini görebiliyoruz, bu da üç grup arasında ortalama kayıp açısından istatistiksel olarak anlamlı bir fark olduğunu gösteriyor. Bu, hipotez testlerimiz için tüm p değerlerinin 0,05’ten küçük olmasıyla tutarlıdır.

Bu özel örnek için aşağıdaki sonuçları çıkarabiliriz:

• C grubunun ortalama değerleri A ve B gruplarının ortalama değerlerinden anlamlı derecede yüksektir.
• B grubunun ortalama değerleri A grubunun ortalama değerlerinden anlamlı derecede yüksektir.

Ek kaynaklar

ANOVA ile Post-Hoc Testini Kullanma Kılavuzu
R’de tek yönlü ANOVA nasıl gerçekleştirilir
R’de iki yönlü ANOVA nasıl gerçekleştirilir