Üç yollu anova: tanım ve örnek

Üç farklı faktörün bir yanıt değişkenini nasıl etkilediğini belirlemek için üç yönlü ANOVA kullanılır.

Üç yönlü ANOVA’lar , tek yönlü ANOVA’dan (yalnızca tek faktörlü) veya iki yönlü ANOVA’dan (yalnızca iki faktörlü) daha az yaygındır, ancak yine de çeşitli alanlarda kullanılmaktadırlar.

Üç yönlü bir ANOVA uyguladığımızda, her faktör ile yanıt değişkeni arasında istatistiksel olarak anlamlı bir ilişki olup olmadığını ve ayrıca faktörler arasında herhangi bir etkileşim etkisi olup olmadığını bilmek isteriz.

Bu eğitimde, üç yönlü ANOVA’yı kullanabileceğiniz çeşitli senaryoların yanı sıra bunun nasıl gerçekleştirileceğine ilişkin bir örnek gösterilmektedir.

Üç yönlü ANOVA ne zaman kullanılmalı?

Üç yönlü ANOVA’yı kullanabileceğiniz bazı senaryolar şunlardır:

Senaryo 1: Botanik

Bir botanikçi (1) güneşe maruz kalmanın, (2) sulama sıklığının ve (3) gübre tipinin bitki büyümesini nasıl etkilediğini belirlemek isteyebilir.

Bu senaryoda üç faktör ve bir yanıt değişkeni olduğundan üç yönlü bir ANOVA gerçekleştirebilir.

Senaryo 2: Perakende

Bir perakende mağazasının yöneticisi, haftanın (1) gününün, (2) mağaza konumunun ve (3) reklam kampanyalarının toplam satışları nasıl etkilediğini belirlemek isteyebilir.

Bu senaryoda üç faktör ve bir yanıt değişkeni olduğundan üç yönlü bir ANOVA gerçekleştirebilir.

Senaryo 3: Tıbbi

Bir doktor (1) cinsiyetin, (2) diyetin ve (3) egzersiz alışkanlıklarının kiloyu nasıl etkilediğini belirlemek isteyebilir.

Bu senaryoda üç faktör ve bir yanıt değişkeni olduğundan üç yönlü bir ANOVA gerçekleştirebilir.

Üç yönlü ANOVA: örnek

Bir araştırmacının antrenman programının, cinsiyetin ve spor bölümünün atlama yüksekliğini etkileyip etkilemediğini belirlemek istediğini varsayalım.

Bunu test etmek için aşağıdaki faktörlerle üç yönlü bir ANOVA gerçekleştirebilir:

• 1. Eğitim programı (program 1 ve program 2)
• 2. Cinsiyet (erkek veya kadın)
• 3. Spor bölümü (bölüm I ve bölüm II)

Tek yanıt değişkeni atlama yüksekliği olacaktır.

Diyelim ki 40 kişi hakkında bu verileri topluyor:

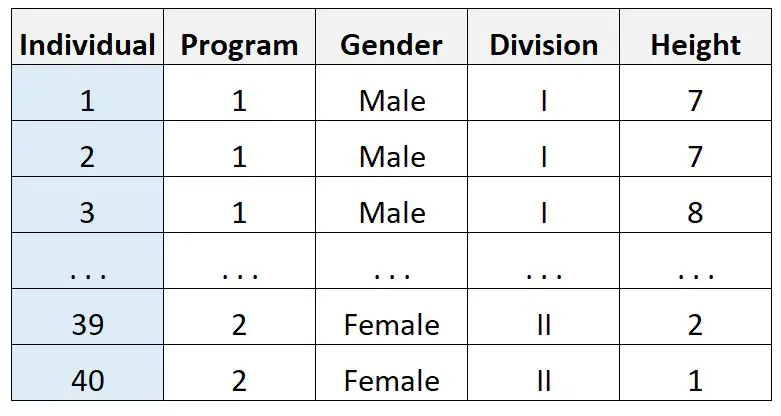
Daha sonra üç yönlü bir ANOVA gerçekleştirmek için istatistiksel yazılımı kullanıyor ve aşağıdaki sonucu alıyor:

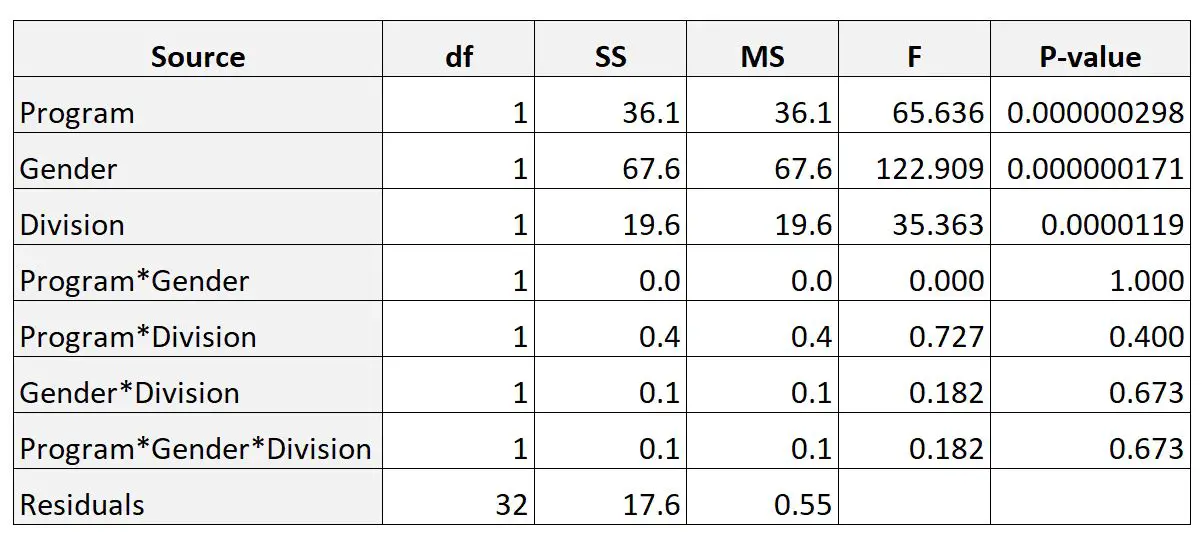
P-Değeri sütunu, her bir faktör için P-değerini ve faktörler arasındaki etkileşimleri görüntüler.

Sonuçlardan, üç faktör arasındaki etkileşimlerin hiçbirinin istatistiksel olarak anlamlı olmadığını görebiliriz.

Ayrıca üç faktörün (Program, Cinsiyet ve Bölüm) her birinin istatistiksel olarak anlamlı olduğunu da görebiliyoruz.

Sonuç olarak, antrenman programı, cinsiyet ve bölümün, oyunculardaki artan sıçrama yüksekliğinin önemli göstergeleri olduğunu söyleyebiliriz.

Ayrıca bu üç faktör arasında anlamlı bir etkileşim etkisinin olmadığını da söyleyebiliriz.

Not : Uygulamada ayrıca her program, cinsiyet ve bölüm için ortalama atlama yüksekliğini de hesaplayacağız, böylece her faktörün hangi düzeylerinin atlama yüksekliğindeki artışla ilişkili olduğunu belirleyebiliriz.

Ek kaynaklar

Aşağıdaki eğitimlerde R ve Python’da üç yönlü ANOVA’nın nasıl gerçekleştirileceği açıklanmaktadır:

R’de üç yönlü ANOVA nasıl gerçekleştirilir
Python’da Üç Yollu ANOVA Nasıl Gerçekleştirilir