Düzgün dağıtıma giriş
Düzgün dağılım, a’dan b’ye kadar olan aralıktaki her değerin aynı oluşma olasılığına sahip olduğu bir olasılık dağılımıdır.
Eğer bir X rastgele değişkeni düzgün bir dağılım izliyorsa, X’in x 1 ile x 2 arasında bir değer alma olasılığı aşağıdaki formülle bulunabilir:
P(x 1 < X < x 2 ) = (x 2 – x 1 ) / (b – a)
Altın:
- x 1 : En düşük faiz değeri
- x 2 : faizin üst değeri
- a: mümkün olan minimum değer
- b: mümkün olan maksimum değer
Örneğin yunusların ağırlığının 100 ila 150 pound arasında eşit olarak dağıldığını varsayalım.
Rastgele bir yunusu seçersek, seçilen yunusun ağırlığının 120 ile 130 pound arasında olma olasılığını belirlemek için yukarıdaki formülü kullanabiliriz:
- P(120 < X < 130) = (130 – 120) / (150 – 100)
- P(120 < X < 130) = 10/50
- P(120 < X < 130) = 0,2
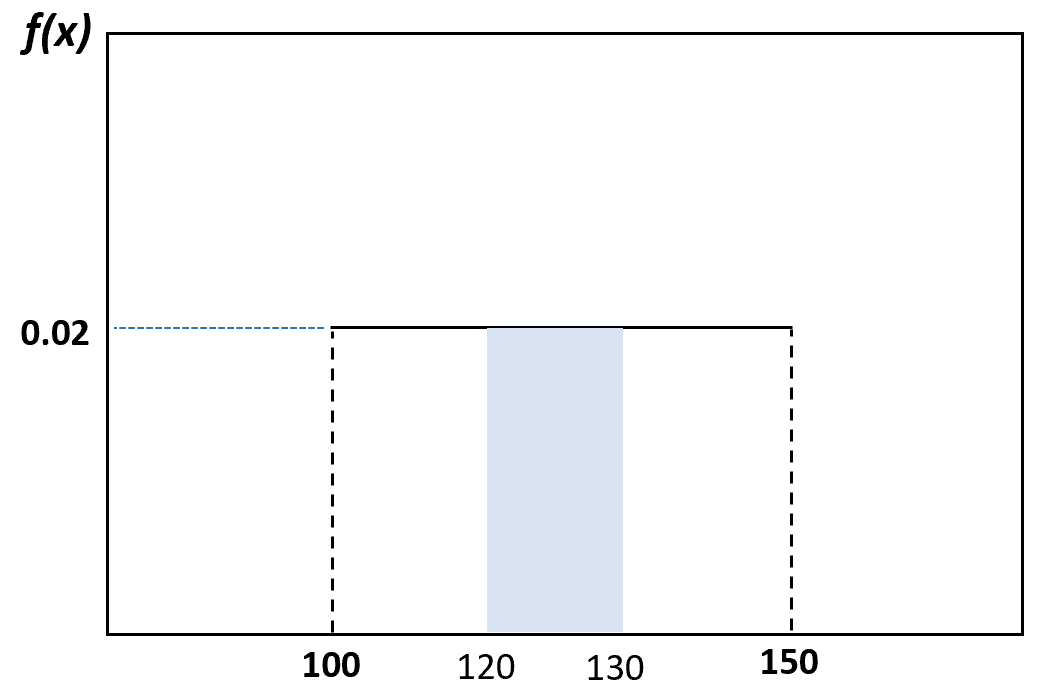
Seçilen yunusun ağırlığının 120 ila 130 pound arasında olma olasılığı 0,2’dir .
Tekdüze dağıtımı görselleştirin
Düzgün dağılımı görselleştirmek için bir yoğunluk grafiği oluşturursak, aşağıdaki çizime benzer:
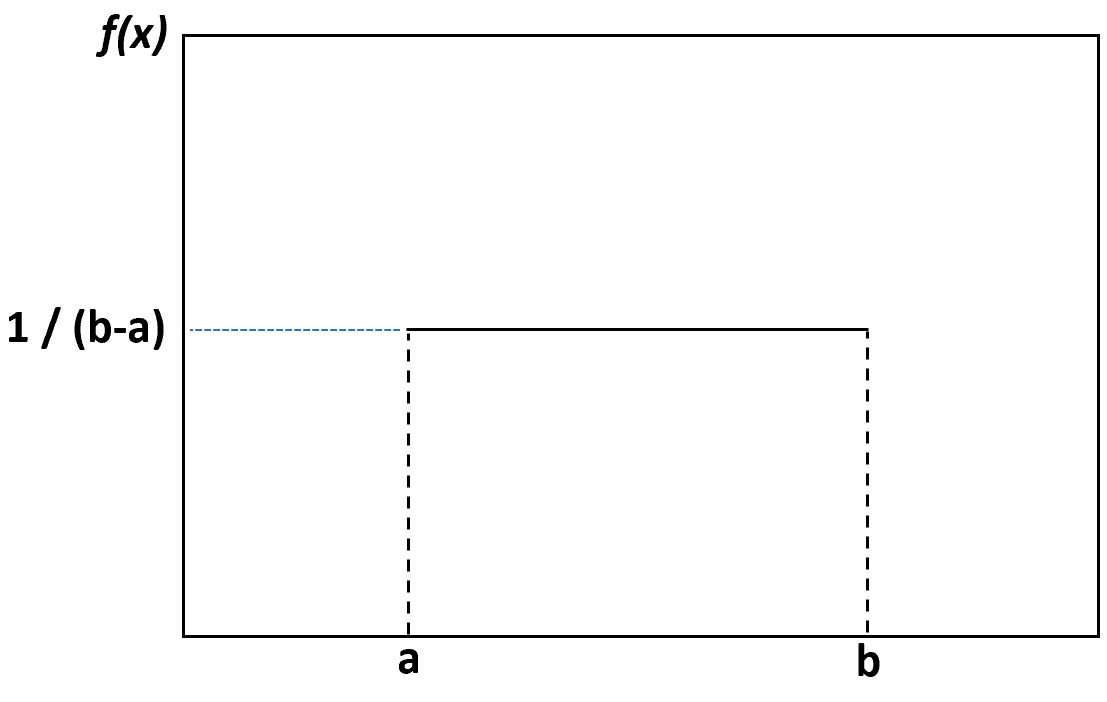
Alt sınır a ile üst sınır b arasındaki her değerin oluşma olasılığı aynıdır ve bu sınırların dışındaki herhangi bir değerin oluşma olasılığı sıfırdır.
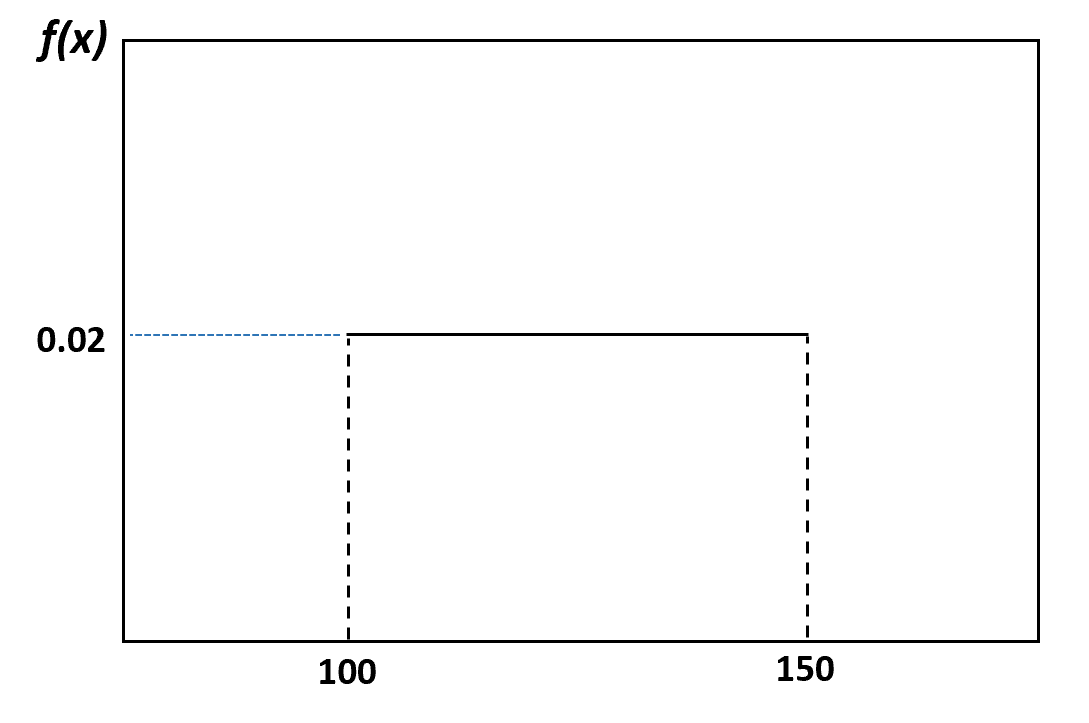
Örneğin bir önceki örneğimizde yunusların ağırlığının 100 ila 150 kilo arasında eşit olarak dağıldığını söylemiştik. Bu dağıtımı şu şekilde görselleştirebilirsiniz:
Rastgele seçilen bir yunusun ağırlığının 120 ile 130 pound arasında olma olasılığı şu şekilde görselleştirilebilir:
Düzgün dağılımın özellikleri
Düzgün dağılım aşağıdaki özelliklere sahiptir:
- Ortalama: (a + b) / 2
- Medyan: (a + b) / 2
- Standart sapma: √ (b – a) 2/12
- Fark: (b – a) 2 / 12
Örneğin yunusların ağırlığının 100 ila 150 pound arasında eşit olarak dağıldığını varsayalım.
Bu dağılım için aşağıdaki özellikleri hesaplayabiliriz:
- Ortalama ağırlık: (a + b) / 2 = (150 + 100) / 2 = 125
- Medyan ağırlık: (a + b) / 2 = (150 + 100) / 2 = 125
- Ağırlığın standart sapması: √ (150 – 100) 2/12 = 14,43
- Ağırlık değişimi: (150 – 100) 2/12 = 208,33
Tekdüzen Dağıtım Uygulamalarıyla İlgili Sorunlar
Düzgün dağılıma ilişkin bilginizi test etmek için aşağıdaki alıştırma problemlerini kullanın.
Soru 1: Her 20 dakikada bir otobüs durağına bir otobüs gelmektedir. Otobüs durağına vardığınızda otobüsün 8 dakika veya daha kısa sürede gelme olasılığı nedir?
Çözüm 1: Minimum bekleme süresi 0 dakika, maksimum bekleme süresi 20 dakikadır. Alt faiz değeri 0 dakika, üst faiz değeri ise 8 dakikadır.
Dolayısıyla olasılığı şu şekilde hesaplayabiliriz:
P(0 < X < 8) = (8-0) / (20-0) = 8/20 = 0,4 .
Soru 2: Bir NBA maçının süresi 120 ila 170 dakika arasında eşit olarak dağıtılmaktadır. Rastgele seçilen bir NBA maçının 155 dakikadan fazla sürme olasılığı nedir?
Çözüm 2: Minimum süre 120 dakika, maksimum süre 170 dakikadır. Alt faiz değeri 155 dakika, üst faiz değeri ise 170 dakikadır.
Dolayısıyla olasılığı şu şekilde hesaplayabiliriz:
P(155 < X < 170) = (170-155) / (170-120) = 15/50 = 0,3 .
Soru 3: Belirli bir kurbağa türünün ağırlığı 15 ila 25 gram arasında eşit olarak dağılmıştır. Rastgele bir kurbağa seçerseniz ağırlığının 17 ile 19 gram arasında olma olasılığı nedir?
Çözüm 3: Minimum ağırlık 15 gram, maksimum ağırlık ise 25 gramdır. Alt faiz değeri 17 gram, üst faiz değeri ise 19 gramdır.
Dolayısıyla olasılığı şu şekilde hesaplayabiliriz:
P(17 < X < 19) = (19-17) / (25-15) = 2/10 = 0,2 .
Not: Bu sorunların her birine verdiğimiz yanıtları kontrol etmek için Tekdüzen Dağılım Hesaplayıcıyı kullanabiliriz.
yazar hakkında
Dr.benjamin anderson
Merhaba, ben Benjamin, emekli bir istatistik profesörü ve Statorials öğretmenine dönüştüm. İstatistik alanındaki kapsamlı deneyimim ve uzmanlığımla, öğrencilerimi Statorials aracılığıyla güçlendirmek için bilgilerimi paylaşmaya can atıyorum. Daha fazlasını bil