Üstel dağılım

İle Dr.benjamin anderson Ağustos 3, 2023 Olasılık 0 Yorum

Bu makalede istatistikte üstel dağılımın ne olduğu ve ne için kullanıldığı anlatılmaktadır. Aynı şekilde üstel dağılımın özelliklerinin neler olduğunu, formüllerini, grafiğini ve çözülmüş bir alıştırmayı bulacaksınız. Ek olarak, çevrimiçi bir üstel dağılım hesaplayıcıyla herhangi bir olasılığı hesaplayabileceksiniz.

Üstel dağılım nedir?

Üstel dağılım, rastgele bir olayın meydana gelmesi için bekleme süresini modellemek için kullanılan sürekli bir olasılık dağılımıdır.

Daha doğrusu üstel dağılım, Poisson dağılımını takip eden iki olay arasındaki bekleme süresini tanımlamamıza olanak tanır. Bu nedenle üstel dağılım Poisson dağılımıyla yakından ilişkilidir.

➤ Bakınız: Poisson dağılımı nedir?

Üstel dağılım, Yunan harfi λ ile temsil edilen karakteristik bir parametreye sahiptir ve incelenen olayın belirli bir süre içinde kaç kez meydana gelmesinin beklendiğini gösterir.

$X\sim \text{Exp}(\lambda)$

Benzer şekilde üstel dağılım da bir arıza meydana gelene kadar geçen süreyi modellemek için kullanılır. Bu nedenle üstel dağılımın güvenilirlik ve hayatta kalma teorisinde çeşitli uygulamaları vardır.

Üstel Dağılım Örnekleri

Artık üstel dağılımın tanımını bildiğimize göre, kavramı daha iyi anlamak için bu tür dağılımın birkaç örneğine bakalım.

Üstel dağılım örnekleri:

Çağrı merkezinde iki çağrı arasında geçen süre.
Bir kişinin belirli bir caddeden ücretsiz bir taksi geçmesine kadar beklemesi gereken süre.
Yeni bir müşterinin mağazaya girmesine kadar geçen süre.
İki farklı kullanıcının bir web sayfasına girmesi arasında geçen süre.
Havaalanında bir uçağın kalkışından diğerinin kalkışına kadar geçen süre.

Üstel dağılım formülü

Üstel dağılım olasılığının hesaplanmasını tanımlayan yoğunluk fonksiyonu formülü, λ çarpı e sayısı üzeri negatif λ çarpı x’e eşittir.

Başka bir deyişle üstel dağılım olasılığını hesaplama formülü aşağıdaki gibidir:

👉 Üstel dağılıma uyan bir değişkenin olasılığını hesaplamak için aşağıdaki hesaplayıcıyı kullanabilirsiniz.

Öte yandan üstel dağılımın kümülatif olasılığını hesaplamak için formül aşağıdaki gibidir:

$P[X\leq x]=1-e^{-\lambda x}$

Üstel dağılım grafiği

Bu bölümde üstel dağılıma ait yoğunluk fonksiyonunun ve dağılım fonksiyonunun grafiksel gösterimini görebilirsiniz.

Aşağıda üstel dağılımın yoğunluk fonksiyonu grafiğinin λ parametresinin değerine bağlı olarak nasıl değiştiğini görebilirsiniz.

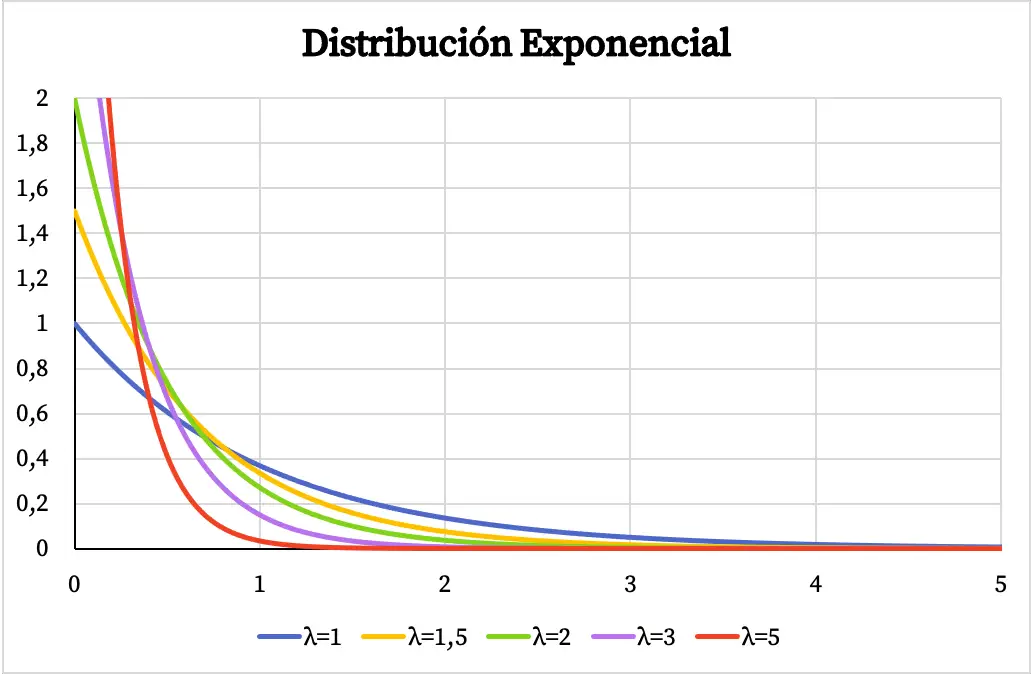
Benzer şekilde üstel dağılımın kümülatif olasılık fonksiyonu da aşağıdaki grafikte görebileceğiniz gibi λ parametresinin değerine bağlıdır:

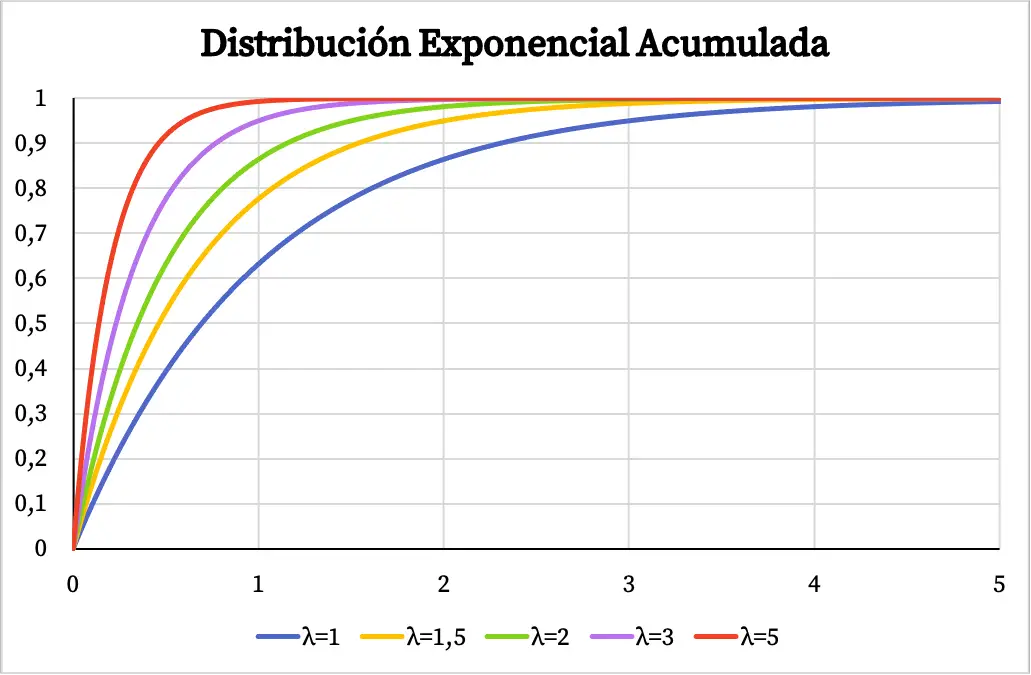
üstel kümülatif dağılım olasılık grafiği

Üstel dağılımla ilgili çözülmüş alıştırma

Ortalama olarak λ=1 kullanıcı/dak belirli bir web sayfasına erişir. İki kullanıcının girişi arasındaki sürenin 3 dakika olma olasılığı nedir? Peki bunun 2 dakikaya eşit veya daha az olma olasılığı?

Bu problemin rastgele değişkenini tanımlayan dağılım üstel bir dağılımdır, çünkü bir olayın meydana geldiği andan (bir kullanıcının web sayfasına girişi) aynı olayın tekrar gerçekleşmesine kadar geçen süreyi inceliyoruz.

$X\sim \text{Exp}(1)$

Bu nedenle, iki farklı kullanıcının girişi arasında geçen sürenin üç dakika olma olasılığını hesaplamak için yoğunluk fonksiyonu formülünü uygulamamız gerekir (yukarıya bakın):

$\begin{aligned}P[X=x]&=\lambda e^{-\lambda x}\\[2ex]P[X=3]&=1\cdot e^{-1\cdot 3}\\[2ex]P[X=3]&=0,05\end{aligned}$

Öte yandan, kümülatif bir olasılığı belirlemek için üstel dağılımın dağılım fonksiyonu formülünü kullanmalıyız:

$\begin{aligned}P[X\leq x]&=1- e^{-\lambda x}\\[2ex]P[X\leq 2]&=1-e^{-1\cdot 2}\\[2ex]P[X\leq 2]&=0,86\end{aligned}$

Üstel dağılımın özellikleri

Üstel dağılım aşağıdaki özelliklere sahiptir:

Üstel dağılım, incelenen olgunun belirli bir süre içinde kaç kez meydana gelmesinin beklendiğini gösteren karakteristik bir parametre olan λ’ya sahiptir.

$X\sim \text{Exp}(\lambda)$

Üstel dağılım negatif bir değer alamaz, dolayısıyla üstel dağılımın alanı sıfırdan büyük veya sıfıra eşit tüm gerçek sayılardan oluşur.

$x\in [0,+\infty)$

Üstel dağılımın ortalaması, λ karakteristik parametresine bölünen sayıya eşittir.

$E[X]=\cfrac{1}{\lambda}$

Üstel dağılımın varyansı, ortalamasının karesidir, dolayısıyla üstel dağılımın varyansı, λ kare katsayısının bire eşdeğerdir.

$Var(X)=\cfrac{1}{\lambda^2 }$

λ değeri ne olursa olsun üstel dağılımın asimetri katsayısı her zaman 2’ye eşittir.

$A=2$

Benzer şekilde herhangi bir üstel dağılımın basıklık katsayısı her zaman 9’a eşittir.

$C=9$

Üstel dağılımın yoğunluk fonksiyonunun formülü şöyledir:

$P[X=x]=\lambda e^{-\lambda x}$

Üstel dağılımın kümülatif olasılık fonksiyonunun formülü aşağıdaki gibidir:

$P[X\leq x]=1-e^{-\lambda x}$

Üstel dağılım, yetersiz bellek özelliğine sahip birkaç olasılık dağılımından biridir. Bu özellik, daha önceki bir olayın meydana gelmesinin, o olayın gelecekte meydana gelme olasılığını etkilemediği anlamına gelir. Örneğin, üstel bir dağılımda, yeni bir kullanıcının bir web sayfasına bir dakikadan daha kısa bir süre içinde erişme olasılığı, kullanıcının yeni girmiş olmasına veya o zamandan beri hiçbir kullanıcının girmemiş olmasına bağlı değildir. on dakikadan fazla.

$P[X>x+y|X>y]=P[X>x]” title=”Rendered by QuickLaTeX.com” height=”19″ width=”254″ style=”vertical-align: -5px;”></p> </p> <h2 class=$ Üstel Dağılım Hesaplayıcı

Olasılığı hesaplamak için λ parametresinin değerini ve x’in değerini aşağıdaki hesap makinesine girin. Hesaplamak istediğiniz olasılığı seçmeniz ve ondalık ayırıcı olarak noktayı kullanarak sayıları (örneğin 0,50) girmeniz gerekir.

yazar hakkında

Dr.benjamin anderson

Merhaba, ben Benjamin, emekli bir istatistik profesörü ve Statorials öğretmenine dönüştüm. İstatistik alanındaki kapsamlı deneyimim ve uzmanlığımla, öğrencilerimi Statorials aracılığıyla güçlendirmek için bilgilerimi paylaşmaya can atıyorum. Daha fazlasını bil