Uyum kalitesi
Bu makale istatistikte uyum iyiliğinin ne olduğunu açıklamaktadır. Benzer şekilde, bir regresyon modelinin uyum iyiliğinin nasıl ölçüleceğini gösterir ve ayrıca uyum iyiliğinin çözülmüş bir uygulamasını görebileceksiniz.
Uyum iyiliği nedir?
İstatistiklerde uyum iyiliği , bir regresyon modelinin veri örneğine ne kadar iyi uyduğudur. Başka bir deyişle, bir regresyon modelinin uyum iyiliği, gözlem seti ile regresyon yoluyla elde edilen değerler arasındaki bağlantının seviyesini ifade eder.
Bu nedenle bir regresyon modelinin uyum iyiliği ne kadar iyi olursa, incelenen verileri o kadar iyi açıklar. Bu nedenle istatistiksel modelin daha iyi uyumunu, daha iyi olmasını istiyoruz.
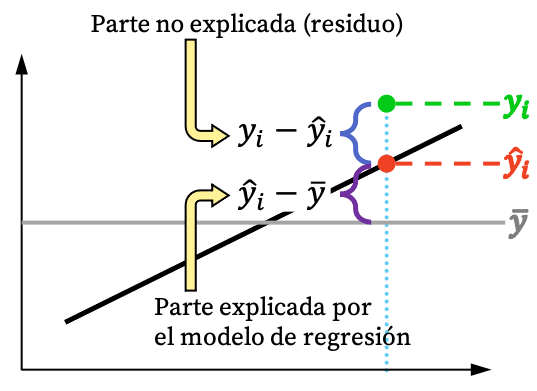
Yukarıdaki görselden de görebileceğiniz gibi bir gözlemin değeri genellikle regresyon modeliyle tam olarak açıklanamaz. Ancak mantıksal olarak regresyon modeli veri kümesinden ne kadar çok şey açıklayabilirse model o kadar iyi uyum sağlar. Kısacası mümkün olduğu kadar sıkı bir regresyon modeliyle ilgileniyoruz.
Bir regresyon modelinin uyum iyiliği
Bir regresyon modelinin uyum iyiliğini belirlemek için genellikle regresyon modeli tarafından açıklanan yüzdeyi gösteren istatistiksel bir katsayı olan belirleme katsayısı kullanılır . Dolayısıyla bir modelin belirleme katsayısı ne kadar yüksek olursa, model veri örneğine o kadar iyi uyarlanacaktır.
![]()
Ancak şunu da belirtmek gerekir ki bir regresyon modeli ne kadar çok değişkene sahip olursa, belirleme katsayısı da o kadar yüksek olacaktır. Bu nedenle, bir modelin uyum iyiliğini ölçmek için düzeltilmiş belirleme katsayısı da sıklıkla kullanılır. Düzeltilmiş belirleme katsayısı, regresyon modeli tarafından açıklanan yüzdeyi gösteren önceki katsayının bir varyasyonudur ve modele dahil edilen her açıklayıcı değişken için cezalandırıcıdır.
![]()
Bu nedenle, iki modeli bir dizi farklı değişkenle karşılaştırmak için düzeltilmiş belirleme katsayısının kullanılması tercih edilir, çünkü modelde yer alan değişkenlerin sayısı dikkate alınır.
Son olarak, genellikle önceki iki katsayıların değerleri kullanılsa da, Ki-kare testinin bir regresyon modelinin uyum iyiliğini ölçmek için de kullanılabileceğini belirtmek gerekir.
İyi uyumun somut örneği
Son olarak, bu istatistiksel kavramı özümsemeyi tamamlamak için ayarlama kalitesi konusunda çözümlenmiş bir alıştırma göreceğiz.
- Aynı veri serisi ile sonuçlarını aşağıdaki tabloda görebileceğiniz iki farklı doğrusal regresyon modeli gerçekleştirilir. Hangi modeli kullanmak en iyisidir?
| Regresyon modeli 1 | Regresyon modeli 2 | |
|---|---|---|
| Determinasyon katsayısı | %57 | %64 |
| Düzeltilmiş belirleme katsayısı | %49 | %43 |
| Açıklayıcı değişkenlerin sayısı | 3 | 7 |
Bu durumda, her iki modelin de doğrusal regresyon modellerinin önceki varsayımlarını karşıladığını varsayıyoruz ve bu nedenle yalnızca modellerin uyum iyiliğini analiz etmemiz gerekiyor.
Regresyon modeli 2, regresyon modeli 1’e göre daha yüksek bir belirleme katsayısına sahiptir, dolayısıyla veri örneğini daha iyi açıklayabildiği için daha iyi bir regresyon modeli olduğu önsel olarak görülmektedir.
Ancak Regresyon Modeli 2’nin modelinde 7 bağımsız değişken bulunurken Regresyon Modeli 1’in yalnızca 3 bağımsız değişkeni vardır. Dolayısıyla Model 2’nin yorumlanması ilk modele göre çok daha karmaşık ve zor olacaktır.
Ek olarak, modeldeki değişken sayısını dikkate alan düzeltilmiş belirleme katsayısına bakarsak, regresyon modeli 1, regresyon modeli 2’den daha yüksek bir düzeltilmiş belirleme katsayısına sahiptir.
Sonuç olarak, düzeltilmiş belirleme katsayısı regresyon modeli 2’den daha yüksek olduğundan regresyon modeli 1’i kullanmak daha iyi olsa da, regresyon modeli 2’nin düzeltilmemiş belirleme katsayısı daha yüksek olduğundan bunun nedeni regresyona çok daha fazla değişken dahil etmeleridir. model 1. model, söz konusu katsayının değerini artıran ancak modelin yorumunu zorlaştıran ve elbette yeni bir değerin tahminini zorlaştıran model.
Farklı sayıda değişken içeren modelleri karşılaştırmak için düzeltilmiş belirleme katsayısını kullanmak en iyisidir çünkü modele eklenen her değişken için ceza verir. Bu örnekte gördüğünüz gibi, düzeltilmemiş belirleme katsayısına göre regresyon modeli 2 daha iyidir, ancak düzeltilmiş belirleme katsayısı sayesinde regresyon modeli 1’in aslında daha iyi olduğunu bilebiliriz.