Varyans

İle Dr.benjamin anderson Ağustos 5, 2023 İstatistik 0 Yorum

Bu yazımızda varyans olarak da adlandırılan varyansın ne olduğunu ve nasıl hesaplandığını açıklayacağız. Varyans hesaplamasının somut bir örneği olan varyans formülünü bulacaksınız ve ayrıca çevrimiçi bir hesap makinesiyle herhangi bir veri kümesinin varyansını hesaplayabileceksiniz.

Ayrıca, farklı bir şekilde yapıldığı için gruplandırılmış verilerin varyansını nasıl bulacağınızı da gösteriyoruz. Son olarak popülasyon varyansı ile örneklem varyansı arasındaki farkı, varyans ile standart sapma arasındaki farkı ve bu istatistiksel ölçümün özelliklerini öğretiyoruz.

Varyans nedir?

İstatistikte varyans, bir rastgele değişkenin değişkenliğini gösteren bir dağılım ölçüsüdür. Varyans, artıkların karelerinin toplamının toplam gözlem sayısına bölünmesine eşittir.

Kalıntının istatistiksel bir veri noktasının değeri ile veri kümesinin ortalaması arasındaki fark olarak anlaşıldığını unutmayın.

Olasılık teorisinde varyansın sembolü Yunanca sigma kare harfidir (σ ² ). Genellikle Var(X) olarak da temsil edilmesine rağmen X , varyansın hesaplandığı rastgele değişkendir.

Genel olarak bir rastgele değişkenin varyans değerinin yorumlanması basittir. Varyans değeri ne kadar büyük olursa veri o kadar dağınık olur. Tam tersi, varyans değeri ne kadar küçükse, veri serisindeki dağılım da o kadar az olacaktır. Ancak varyansı yorumlarken aykırı değerlere dikkat edilmelidir çünkü bunlar varyans değerini çarpıtabilir.

varyans, dağılım dışında dikkate alınan diğer ölçüler ise aralık, standart sapma, ortalama sapma ve değişim katsayısıdır.

Boşluk nasıl hesaplanır

Farkı hesaplamak için aşağıdaki adımların gerçekleştirilmesi gerekir:

Veri kümesinin aritmetik ortalamasını bulun.
Değerler ile veri kümesinin ortalaması arasındaki fark olarak tanımlanan artıkları hesaplayın.
Geri kalan her şeyin karesini alın.
Önceki adımda hesaplanan tüm sonuçları ekleyin.
Toplam veri sayısına bölün. Elde edilen sonuç veri serisinin varyansıdır.

Sonuç olarak, bir veri kümesinin varyansını hesaplama formülü şöyledir:

Altın:

$X$

varyansını hesaplamak istediğiniz rastgele değişkendir.
$x_i$

veri değeri

$i$

.
$n$

toplam gözlem sayısıdır.
$\overline{X}$

rastgele değişkenin ortalamasıdır

$X$

.

👉Herhangi bir veri setinin varyansını hesaplamak için aşağıdaki hesaplayıcıyı kullanabilirsiniz.

Bu nedenle, bir veri serisinden varyansı çıkarmak için aritmetik ortalamanın nasıl hesaplandığını bilmeniz önemlidir. Bunu nasıl yapacağınızı hatırlamıyorsanız, yukarıda bağlantısı verilen makaleye göz atabilirsiniz.

Sapma örneği

Artık varyansın tanımını bildiğimize göre, bir veri serisinin varyansının nasıl elde edildiğini görebilmeniz için adım adım bir alıştırma çözeceğiz.

Çok uluslu bir şirketin son beş yılda elde ettiği ekonomik sonuç malum, çoğunluğu kâr etti ama bir yıl ciddi zararlar verdi: 11,5, 2, -9, 7 milyon euro. Bu veri setinin varyansını hesaplayın.

Yukarıdaki açıklamada gördüğümüz gibi bir veri serisinin varyansını bulmak için yapmamız gereken ilk şey aritmetik ortalamasını hesaplamaktır:

$\overline{X}=\cfrac{11+5+2+(-9)+7}{5}=3,2$

Verilerin ortalama değerini bildiğimizde varyans formülünü kullanabiliriz:

$Var(X)=\cfrac{\displaystyle\sum_{i=1}^n\left(x_i-\overline{X}\right)^2}{n}$

Alıştırma beyanının sağladığı verileri formülde değiştiririz:

$Var(X)=\cfrac{\displaystyle (11-3,2)^2+(5-3,2)^2+(2-3,2)^2+(-9-3,2)^2+(7-3,2)^2}{5}$

Son olarak geriye kalan tek şey varyansı hesaplamak için gerekli işlemleri çözmektir:

$\begin{aligned}Var(X)&=\cfrac{7,8^2+1,8^2+(-1,2)^2+(-12,2)^2+3,8^2}{5}\\[2ex]&=\cfrac{60,84+3,24+1,44+148,84+14,44}{5}\\[2ex]&= \cfrac{228,8}{5} \\[2ex]&=45,76 \ \text{millones de euros}^2\end{aligned}$

Varyans birimlerinin istatistiksel verilerle aynı birimler olduğunu ancak kareleri olduğunu unutmayın; bu nedenle bu veri grubunun varyansı 45,76 milyon Euro ^2’dir .

Boşluk Hesaplayıcı

Varyansını hesaplamak için aşağıdaki hesap makinesine bir istatistiksel veri seti girin. Veriler bir boşlukla ayrılmalı ve ondalık ayırıcı olarak nokta kullanılarak girilmelidir.

Gruplandırılmış veriler için varyans

Aralıklara göre gruplandırılmış verilerin varyansını hesaplamak için aşağıdaki adımlar izlenmelidir:

Gruplandırılmış verilerin ortalamasını bulun.
Gruplandırılmış verilerin artıklarını hesaplayın.
Geri kalan her şeyin karesini alın.
Önceki her sonucu aralığının frekansıyla çarpın.
Önceki adımda elde edilen tüm değerlerin toplamını ekleyin.
Toplam gözlem sayısına bölün. Ortaya çıkan sayı, gruplandırılmış verilerin varyansıdır.

Başka bir deyişle, aralıklara göre gruplandırılmış verilerin varyansını hesaplama formülü aşağıdaki gibidir:

$Var(X)=\cfrac{\displaystyle\sum_{i=1}^n\left(x_i-\overline{X}\right)^2\cdot f_i }{n}$

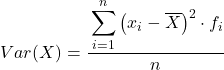
Normalde yukarıdaki formül kullanılsa da aşağıdaki cebirsel ifade de eşdeğer olarak kullanılabilir:

$Var(X)=\cfrac{\displaystyle\sum_{i=1}^n x_i^2\cdot f_i }{n}-\overline{X}^2$

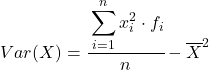
Örnek olarak aşağıdaki gruplandırılmış veri serilerinin varyansını bulacağız:

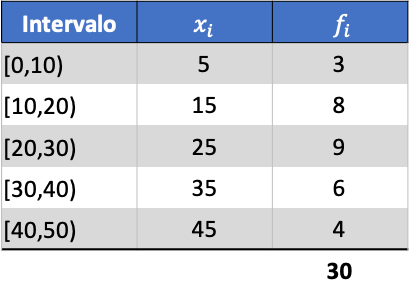
aralıklar halinde gruplandırılmış veriler

Öncelikle gruplandırılmış verilerin ortalamasını belirlememiz gerekiyor. Bunu yapmak için, frekans tablosuna sınıf işaretinin ve frekansın çarpımını içeren bir sütun ekliyoruz:

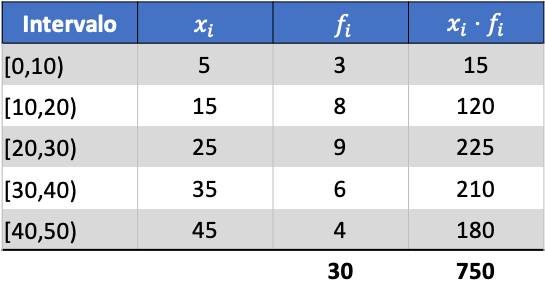
Artık eklenen sütunun toplamını toplam veri sayısına bölerek gruplandırılmış verilerin ortalamasını hesaplıyoruz:

$\overline{X}=\cfrac{\displaystyle\sum_{i=1}^n x_i\cdot f_i}{n}=\cfrac{750}{30}=25$

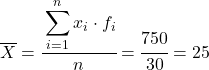
Hesaplanan verilerin ortalamasından aşağıdaki üç sütunu ekleyebiliriz:

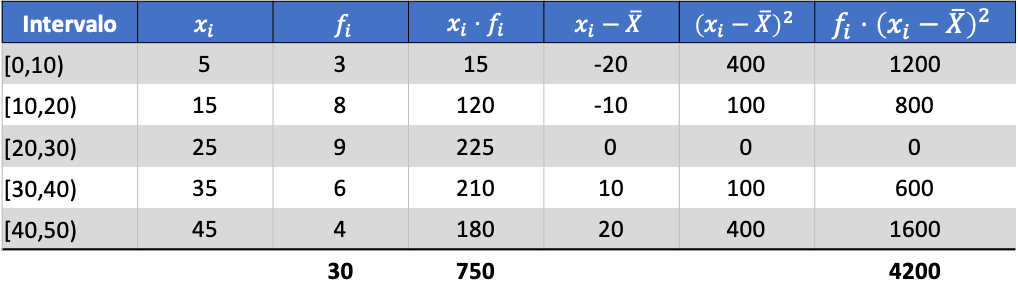
Yani havuzlanmış veri setinin varyansı, son sütunun toplamının gözlemlenen verilerin toplam sayısına bölünmesiyle elde edilir:

$Var(X)=\cfrac{\displaystyle\sum_{i=1}^n\left(x_i-\overline{X}\right)^2\cdot f_i }{n}=\cfrac{4200}{30}=140$

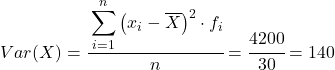
Varyans ve standart sapma

Varyans ve standart sapma (veya standart sapma) iki dağılım ölçüsüdür ve bu nedenle her ikisi de veri setinin dağılım derecesini gösterir. Ancak varyans ile standart sapma arasındaki fark, genel olarak varyansın standart sapmanın karesi olması nedeniyle daha büyük değerlere sahip olmasıdır.

Standart sapma genellikle Yunanca sigma (σ) harfiyle temsil edilir ve bu nedenle varyans, bu iki dağılım ölçüsü arasında var olan matematiksel ilişki olduğundan sigma kare (σ ² ) harfiyle temsil edilir.

$Var(X)=\sigma^2$

Yani bir veri kümesinin varyans değerini hesapladıktan sonra, varyansın karekökünü alarak aynı kümenin standart sapma değerini kolayca bulabilirsiniz.

$\sigma=\sqrt{\sigma^2}$

Popülasyon varyansı ve örneklem varyansı

Mantıksal olarak popülasyon varyansı , istatistiksel bir popülasyonun varyansının hesaplanmasını ifade eder ve bunun yerine, bir numunenin varyansının hesaplanmasına örnek varyansı uygulanır. Ancak popülasyon varyans formülü örneklem varyans formülünden farklı olduğundan bunlar iki farklı kavramdır.

Normalde varyans alıştırmalarında, eğer bize aksini söylemezlerse, sağlanan veri setinin varyansını bulmak için makalenin başında açıkladığımız popülasyon varyans formülünü kullanmamız gerekir:

$\sigma^2=\cfrac{\displaystyle\sum_{i=1}^n\left(x_i-\overline{X}\right)^2}{n}$

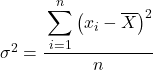
Ancak bazı problemlerde istatistiksel verileri örnek olarak değerlendirmeniz istenebilir, bu durumda örnek varyans formülünü kullanmamız gerekir:

$s^2=\cfrac{\displaystyle\sum_{i=1}^n\left(x_i-\overline{X}\right)^2}{n-1}$

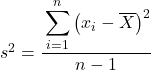
Bir popülasyon varyansının hesaplandığını belirtmek için bunun Yunanca σ harfiyle gösterildiğini, ancak bir örneklem varyansı hesaplanırken s harfinin kullanıldığını unutmayın.

Gördüğünüz gibi iki formül arasındaki tek fark, bir örneklemin varyansını toplam gözlem sayısından 1 çıkararak bölmemiz gerekiyor, örneğin toplamda 30 veri öğesi varsa 29’a böleceğiz. Ancak payın hesaplanması tamamen aynı şekilde yapılır.

Varyans özellikleri

Varyans aşağıdaki özelliklere sahiptir:

Herhangi bir rastgele değişkenin varyansı her zaman sıfırdan büyük veya sıfıra eşit olacaktır. Aynı şekilde varyansın sıfır olması tüm istatistiksel verilerin aynı olduğu anlamına gelir.

$Var(x)\ge 0$

Açıkçası, tek bir değerin varyansı sıfırdır.

$Var(a)=0\qquad a\in \mathbb{R}$

Bir skalerin çarpımının bir değişkene göre varyansı, o skalerin karesinin değişkenin varyansının çarpımına eşittir.

$Var(aX)=a^2\cdot Var(X)\qquad a\in \mathbb{R}$

İki bağımlı değişkenin toplamının varyansı, her bir değişkenin ayrı ayrı varyansının toplamı artı iki değişken arasındaki kovaryansın iki katına eşittir.

$Var(X+Y)=Var(X)+Var(Y)+2Cov(X,Y)$

Sonuç olarak, eğer iki değişken bağımsızsa, toplamlarının varyansını belirlemek için varyanslarının eklenmesi yeterlidir:

$Var(X+Y)=Var(X)+Var(Y)$

Sapma aynı zamanda aşağıdaki formül kullanılarak matematiksel beklentiyle de tanımlanabilir:

$Var(X)=E\bigl[(X-\overline{X})^2\bigr]$

yazar hakkında

Dr.benjamin anderson

Merhaba, ben Benjamin, emekli bir istatistik profesörü ve Statorials öğretmenine dönüştüm. İstatistik alanındaki kapsamlı deneyimim ve uzmanlığımla, öğrencilerimi Statorials aracılığıyla güçlendirmek için bilgilerimi paylaşmaya can atıyorum. Daha fazlasını bil