Varyans için hipotez testi

İle Dr.benjamin anderson Ağustos 3, 2023 İstatistik 0 Yorum

Bu makale varyans için hipotez testinin ne olduğunu açıklamaktadır. Böylece, varyans hipotezi testinin formülünü ve ayrıca adım adım çözülen bir alıştırmayı bulacaksınız.

Varyans için hipotez testi nedir?

Varyans için hipotez testi, bir popülasyon varyansının sıfır hipotezinin reddedilip reddedilmeyeceğini belirlemek için kullanılan istatistiksel bir yöntemdir. Başka bir deyişle varyans hipotez testi, bir popülasyonun varyansının değeri hakkındaki hipotezi reddetmek veya kabul etmek için kullanılır.

Spesifik olarak, varyans için hipotez testi istatistiğinin değerine ve seçilen anlamlılık düzeyine bağlı olarak sıfır hipotezi reddedilir veya kabul edilir.

Hipotez testinin birçok isimle anıldığını unutmayın; buna hipotez karşıtlıkları, hipotez testi veya anlamlılık testi de denilebilir.

Varyans için Hipotez Testi Formülü

Varyans için hipotez testi istatistiği, örneklem büyüklüğü eksi örnek varyansının bir katı arasındaki farka eşittir ve popülasyon varyansının önerilen değerine bölünür. Varyans için hipotez testi istatistiği ki-kare dağılımına sahiptir.

Dolayısıyla varyans için hipotez testi istatistiğini hesaplama formülü aşağıdaki gibidir:

$\chi^2=\cfrac{(n-1)s^2}{\sigma^2}$

Altın:

$\chi^2$

ki-kare dağılımına sahip varyans için hipotez test istatistiğidir.
$n$

örneklem büyüklüğüdür.
$s^2$

örnek varyansıdır.
$\sigma^2$

önerilen popülasyon varyansıdır.

İstatistiğin sonucunun yorumlanabilmesi için elde edilen değerin testin kritik değeri ile karşılaştırılması gerekir.

Varyans için hipotez testi iki kuyruklu ise, istatistik kritik değerden büyükse sıfır hipotezi reddedilir.
$\chi_{1-\alpha/2|n-1}^2$

veya kritik değerin altındaysa

$\chi_{\alpha/2|n-1}$

.
Varyans için hipotez testi sağ kuyrukla eşleşiyorsa, istatistik kritik değerden büyükse sıfır hipotezi reddedilir
$\chi_{1-\alpha|n-1}^2$

.
Varyans için hipotez testi sol kuyrukla eşleşirse, istatistik kritik değerden küçükse sıfır hipotezi reddedilir
$\chi_{\alpha|n-1}$

.

$\begin{array}{l}H_1: \sigma^2\neq \sigma_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } \chi^2>\chi^2_{1-\alpha/2|n-1}\text{ se rechaza } H_0\\[3ex]H_1: \sigma^2\neq \sigma_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si }\chi^2<\chi^2_{\alpha/2|n-1}\text{ se rechaza } H_0 \\[3ex]H_1: \sigma^2> \sigma_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } \chi^2>\chi^2_{1-\alpha|n-1}\text{ se rechaza } H_0\\[3ex]H_1: \sigma^2< \sigma_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } \chi^2<\chi^2_{\alpha|n-1}\text{ se rechaza } H_0\end{array}$

Varyansa ilişkin kritik hipotez testi değerleri ki-kare dağılım tablosundan elde edilir. Ki-kare dağılımı için serbestlik derecesinin örneklem büyüklüğü eksi 1 olduğuna dikkat edin.

Varyans için Gerçek Dünyadan Hipotez Testi Örneği

Varyans hipotezi testinin tanımını ve formülünün ne olduğunu gördükten sonra kavramı özümsemeyi tamamlamak için somut bir örnek göreceğiz.

Bir fabrikada, bir arabanın parçalarını yüksek hassasiyetle üreten bir makine vardır. Ancak artık uzaklaştığı ve artık 8 ^mm2’den büyük aralıklı parçalar ürettiğinden şüpheleniliyor. Bu hipotezi çürütmek için 25 parçalık bir numune analiz edilmiştir ve numune varyansı 9,1 ^mm2’dir . Başlangıç hipotezi α=0,05 anlamlılık düzeyiyle reddedilebilir mi?

Bu varyans hipotezi testi için sıfır hipotezi ve alternatif hipotez aşağıdaki gibidir:

$\begin{cases}H_0: \sigma^2=8 \\[2ex] H_1:\sigma^2>8 \end{cases}” title=”Rendered by QuickLaTeX.com” height=”65″ width=”101″ style=”vertical-align: 0px;”> Sıfır hipotezinin reddedilip reddedilemeyeceğini belirlemek için yukarıda gördüğümüz formülü kullanarak varyansa ilişkin hipotez testi istatistiğini hesaplıyoruz: <p class=$ $\chi^2=\cfrac{(n-1)s^2}{\sigma^2}$

$\chi^2=\cfrac{(25-1)\cdot 9,1}{8}$

$\chi^2=27,3$

Şimdi Ki-kare dağılım tablosunda 24 serbestlik derecesi için sağ kuyruğa karşılık gelen kritik değeri ve α=0,05 anlamlılık düzeyini arıyoruz:

$\begin{array}{c}\chi^2_{1-\alpha|n-1}=\ \color{orange}\bm{?}\color{black}\\[2ex]\chi^2_{0,95|24}=36,415\end{array}$

Dolayısıyla hesaplanan istatistik, testin kritik değerinden küçüktür ve bu nedenle varyans hipotezi testinin sıfır hipotezi reddedilmez, aksine alternatif hipotez reddedilir.

$27,3<36,415 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{No se rechaza } H_0$

➤ Bakınız: Popülasyon ortalaması için hipotez testi
➤ Bakınız: Popülasyon oranı için hipotez testi

İki popülasyonun varyansı için hipotez testi

İki popülasyon varyans hipotezi testi, iki farklı popülasyonun varyanslarının eşit olduğu hipotezini reddetmek veya kabul etmek için kullanılır.

Dolayısıyla, iki popülasyonun varyansına ilişkin bir hipotez testinin sıfır hipotezi her zaman aşağıdaki gibidir:

$H_0: \sigma^2_1=\sigma^2_2$

Alternatif hipotez ise üç seçenekten biri olabilir:

$\begin{array}{l}H_1:\sigma^2_1\neq \sigma^2_2\\[2ex]H_1:\sigma^2_1>\sigma^2_2\\[2ex]H_1:\sigma^2_1<\sigma^2_2\end{array}$

Bu durumda, iki popülasyonun varyansı için hipotez testi istatistiğini hesaplama formülü şöyledir:

$F=\cfrac{s_1^2}{s_2^2}$

Altın:

$F$

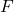
iki popülasyonun varyansı için F dağılımını takip eden hipotez test istatistiğidir.
$\sigma_1^2$

popülasyon 1’in varyansıdır.
$\sigma_2^2$

popülasyon 2’nin varyansıdır.
$s_1^2$

örnek 1’in varyansıdır.
$s_2^2$

örnek 2’nin varyansıdır.
$n_1$

örneklem büyüklüğü 1’dir.
$n_2$

örneklem büyüklüğü 2’dir.

Snedecor F dağılımı simetrik olmadığından sıfır hipotezi aşağıdaki kriterlere göre reddedilir:

[latex]\begin{array}{l}H_1: \sigma_1^2\neq \sigma_2^2 \ \color{orange}\bm{\longrightarrow}\color{siyah} \ \text{Si } F>F_{ 1-\alpha/2|n_1-1|n_2-1}\text{ geri döndü } H_0\\[3ex]H_1: \sigma_1^2\neq \sigma_2^2 \ \color{orange}\bm{\longrightarrow }\color{siyah} \ \text{Eğer }F \sigma_2^2 \ \\color{turuncu}\bm{\longrightarrow}\color{siyah} \ \text{If } F>F_{1-\alpha|n_1-1|n_2-1}\text{ geri döndü } H_0\\[3ex]H_1: \sigma_1^2< \sigma_2^2 \ \color{turuncu}\bm{\longrightarrow}\color{siyah} \ \text{Si } F

yazar hakkında

Dr.benjamin anderson

Merhaba, ben Benjamin, emekli bir istatistik profesörü ve Statorials öğretmenine dönüştüm. İstatistik alanındaki kapsamlı deneyimim ve uzmanlığımla, öğrencilerimi Statorials aracılığıyla güçlendirmek için bilgilerimi paylaşmaya can atıyorum. Daha fazlasını bil