Belirli bir alanda z puanları nasıl bulunur (örneklerle)

Normal dağılım eğrisi altında belirli bir alana karşılık gelen z puanını bulmanın üç yolu vardır

1. z tablosunu kullanın.

2. Z puanı yüzdelik hesaplayıcısını kullanın.

3. TI-84 hesap makinesinde invNorm() işlevini kullanın.

Aşağıdaki örnekler, normal dağılım eğrisi altında belirli bir alana karşılık gelen z-puanını bulmak için bu yöntemlerin her birinin nasıl kullanılacağını gösterir.

Örnek 1: Soldaki Z puanının verilen alanını bulun

Soldaki dağılım alanının %15,62’sini temsil eden z-puanını bulun.

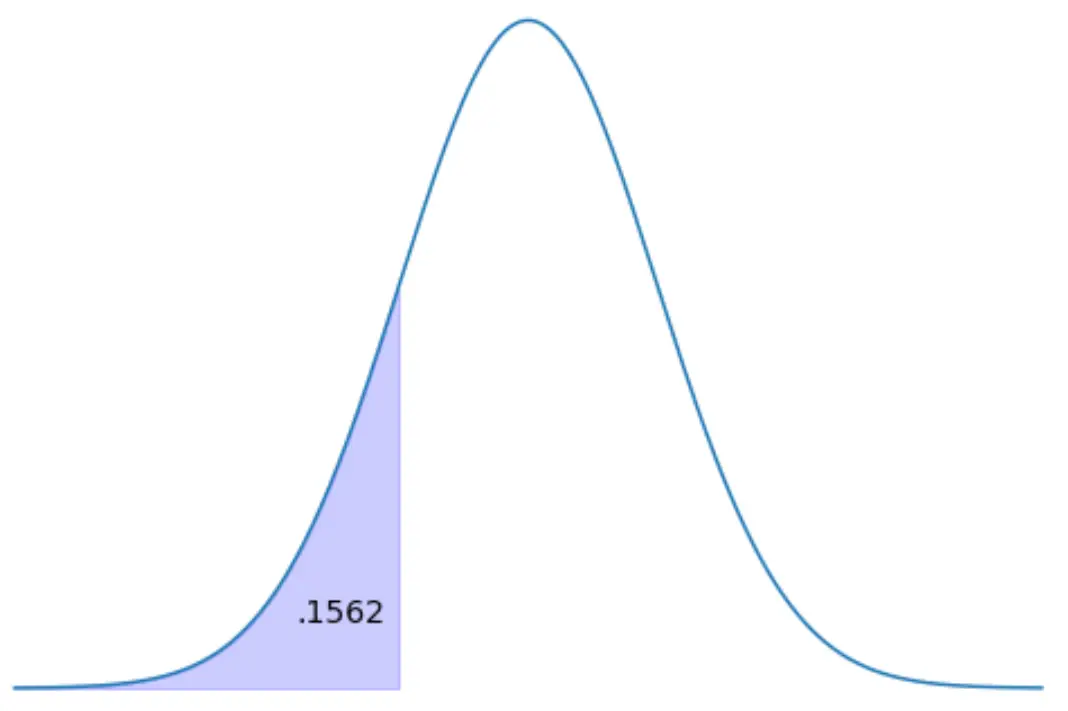
Yöntem 1: z tablosunu kullanın.

Z tablosunda 0,1562 değerine karşılık gelen z puanı -1,01’dir .

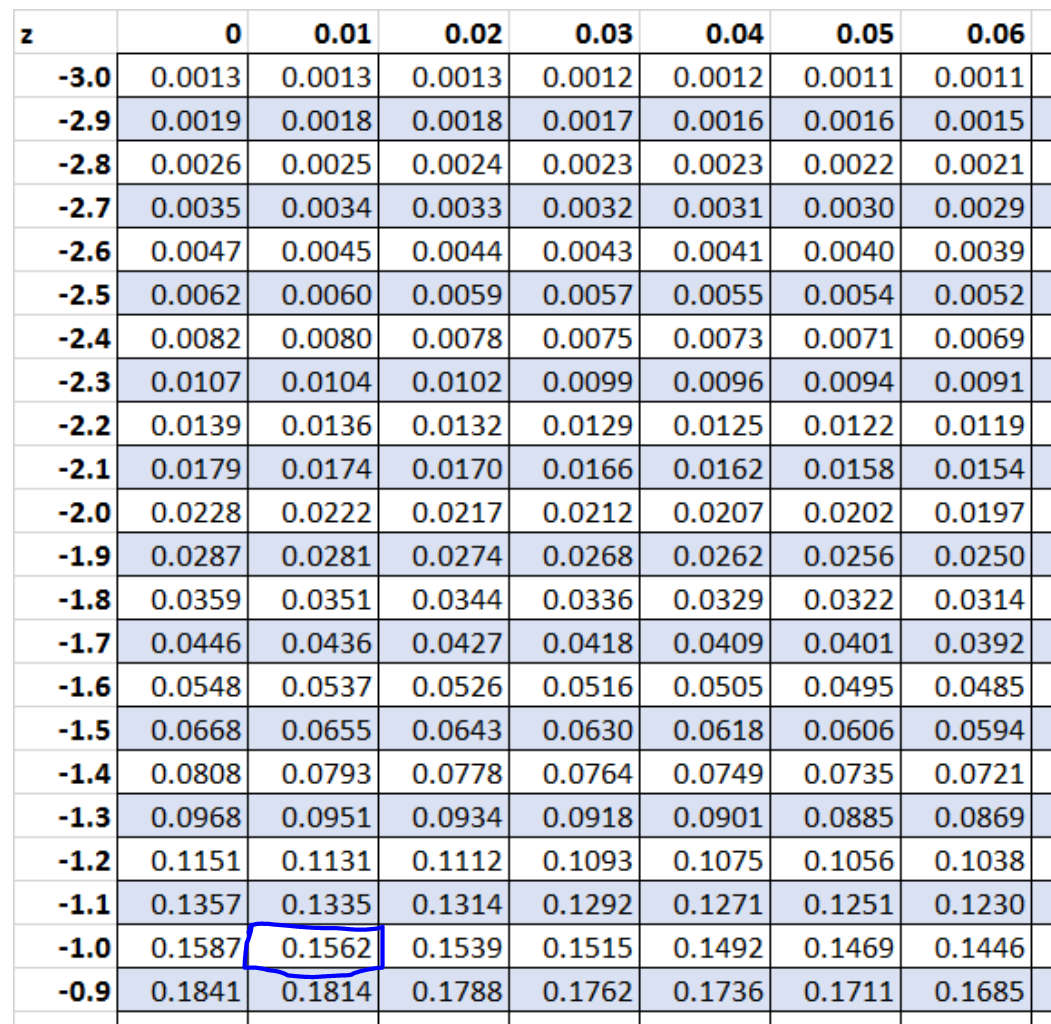
2. Z puanı yüzdelik hesaplayıcısını kullanın.

Z-puanı yüzdelik hesaplayıcısına göre 0,1562 yüzdelik dilimine karşılık gelen z-puanı -1,01’dir .

3. TI-84 hesap makinesinde invNorm() işlevini kullanın.

TI-84 hesap makinesinde invNorm() işlevi kullanıldığında, soldaki 0,1562 alanına karşılık gelen z puanı -1,01 olur.

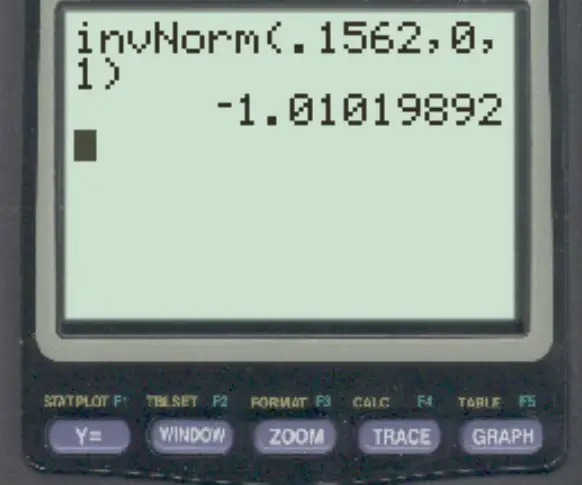
Her üç yöntemin de aynı sonuca yol açtığını unutmayın.

Örnek 2: Sağda verilen Z puanı alanını bulun

Sağdaki dağılım alanının %37,83’ünü temsil eden z-puanını bulun.

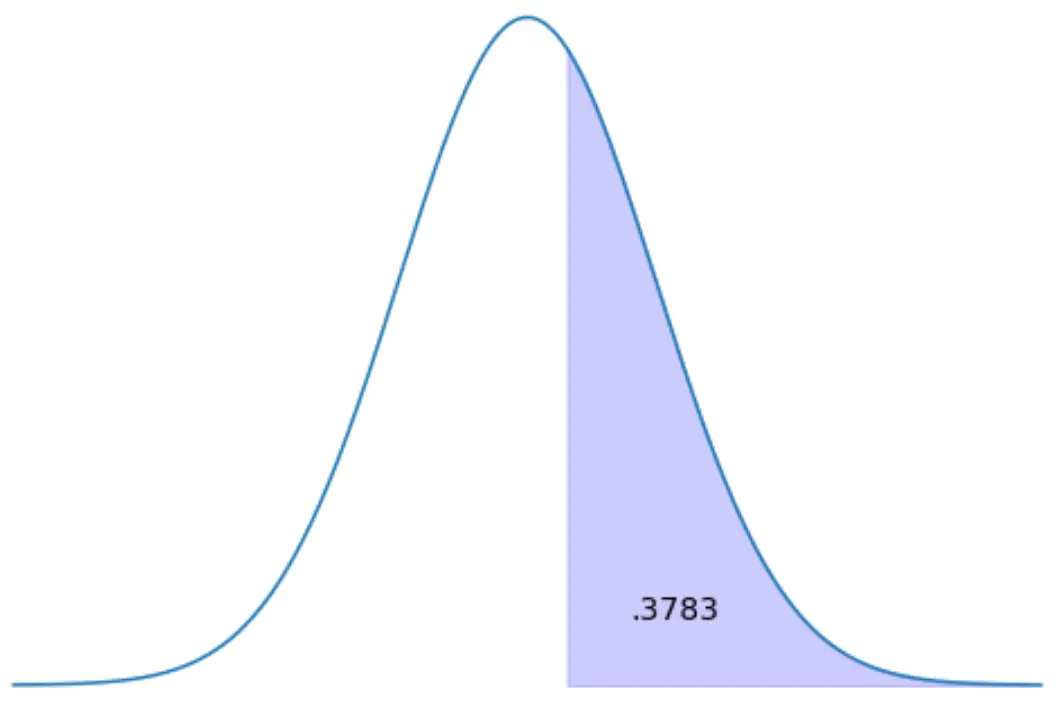
Yöntem 1: z tablosunu kullanın.

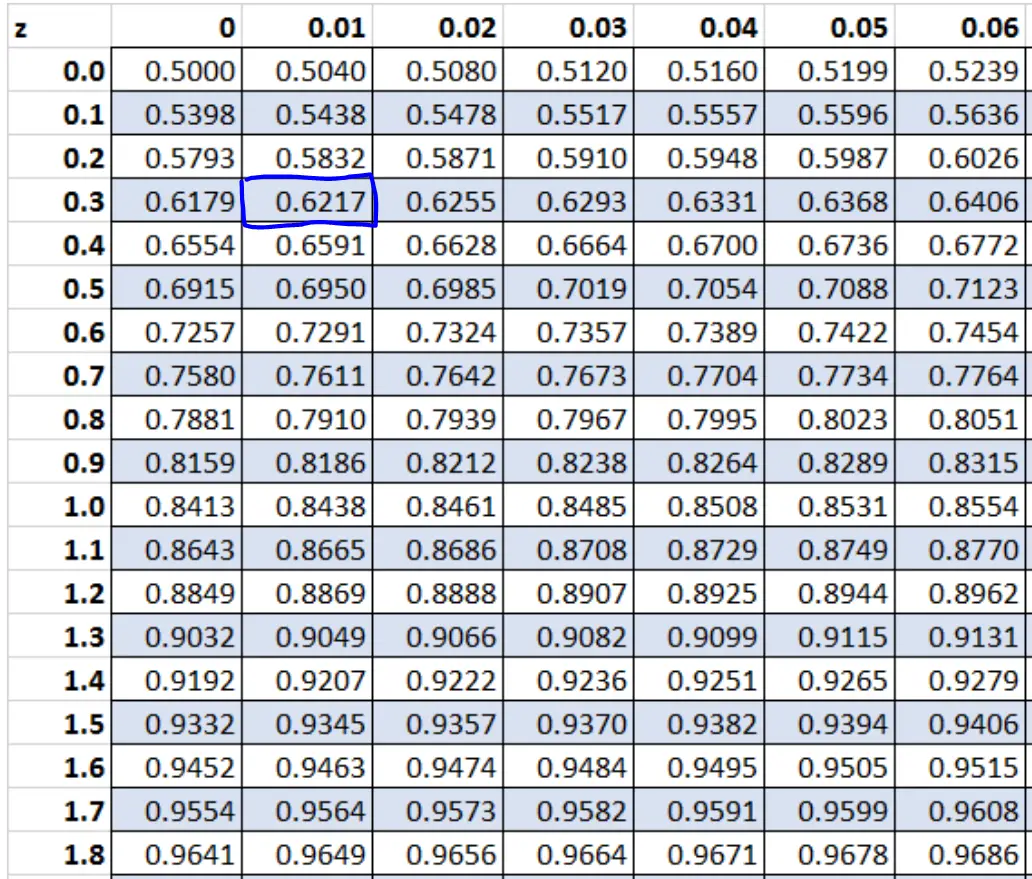
Z grafiği, farklı z puanlarının solundaki alanı gösterir. Yani sağdaki alanın 0,3783 olduğunu biliyorsak soldaki alan 1 – 0,3783 = 0,6217 olur.

Z-tablosunda 0,6217 değerine karşılık gelen z-puanı 0,31’dir.

2. Z puanı yüzdelik hesaplayıcısını kullanın.

Z-puanı yüzdelik hesaplayıcısına göre 0,6217 yüzdelik dilimine karşılık gelen z-puanı . 3099 .

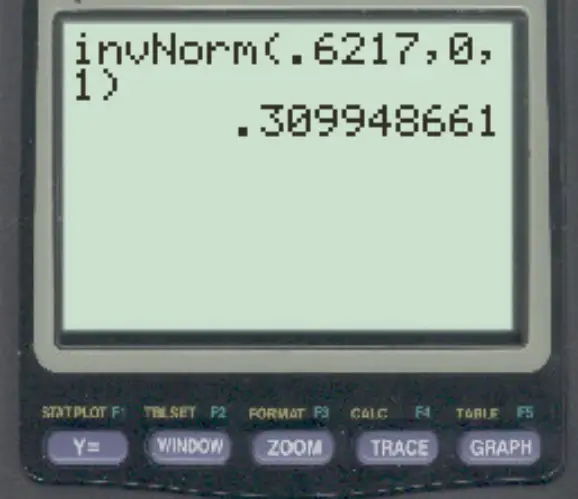
3. TI-84 hesap makinesinde invNorm() işlevini kullanın.

Bir TI-84 hesap makinesinde invNorm() işlevini kullanarak, soldaki 0,6217 alanına karşılık gelen z puanı 0,3099 olur.

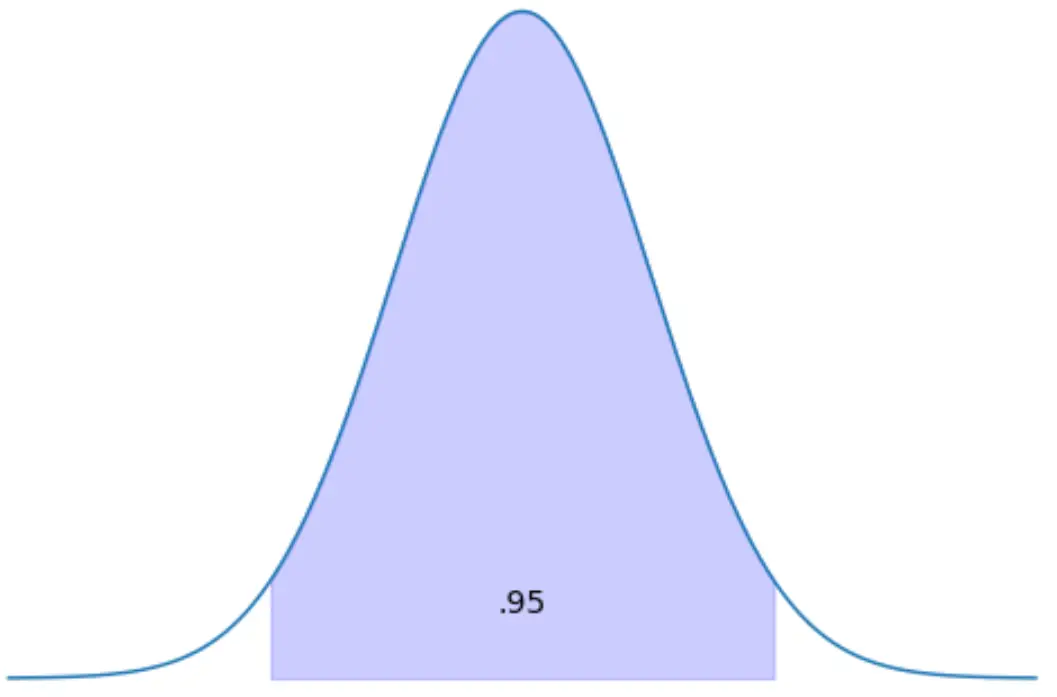
Örnek 3: İki değer arasındaki alanda Z puanlarını bulma

Aralarında dağılım alanının %95’ine sahip olan z puanlarını bulun.

Yöntem 1: z tablosunu kullanın.

Eğer dağılımın %95’i iki z-puanı arasında yer alıyorsa bu, dağılımın %5’inin z-puanlarının dışında olduğu anlamına gelir.

Yani dağılımın %2,5’i z puanlarından birinden düşük, %2,5’i ise diğer z puanlarından yüksek.

Böylece z tablosunda 0,025’e bakabiliriz. Z-tablosunda 0,025’e karşılık gelen z-puanı -1,96’dır .

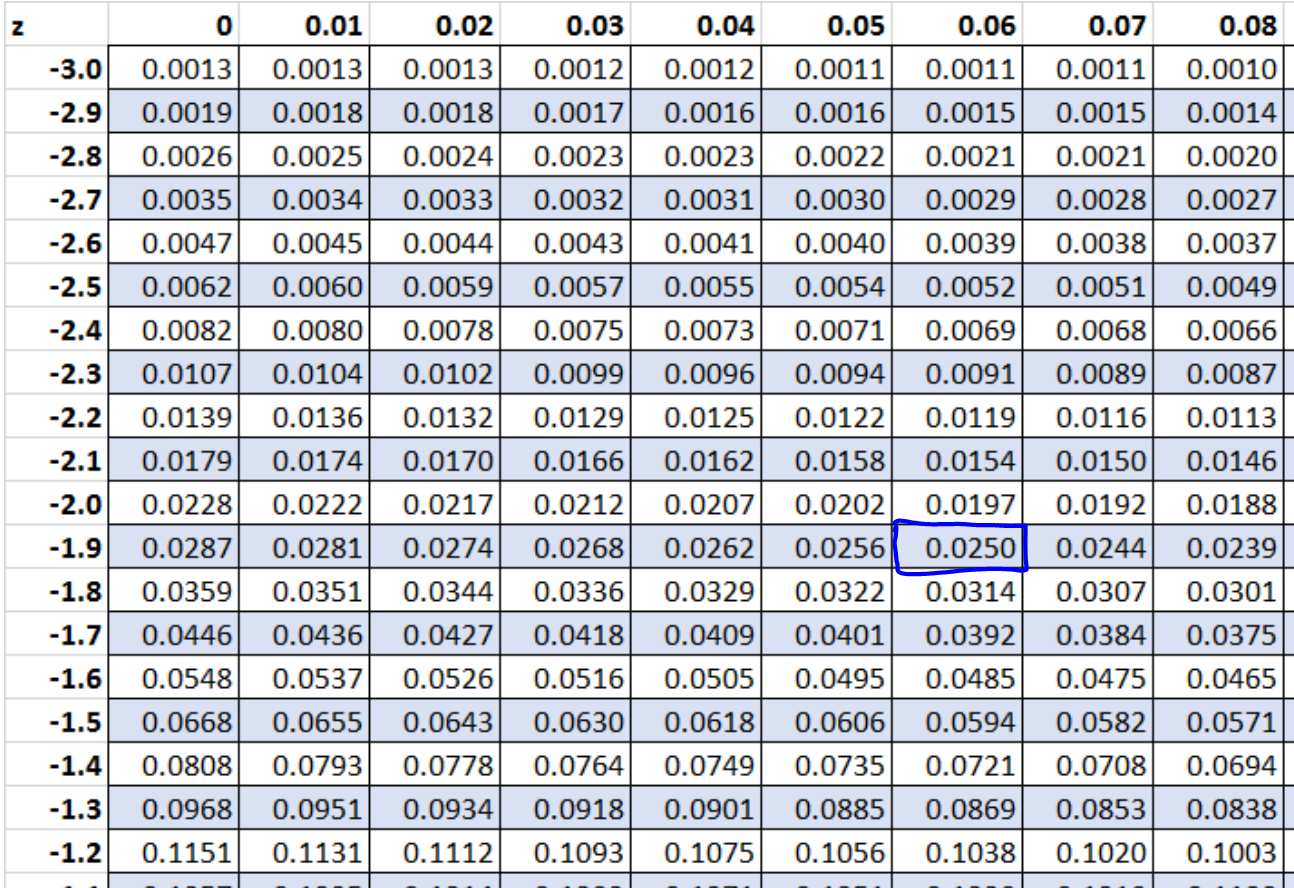
Yani aralarındaki dağılımın %95’ini oluşturan z puanları -1,96 ile 1,96’dır .

2. Z puanı yüzdelik hesaplayıcısını kullanın.

Z-puanı yüzdelik hesaplayıcısına göre 0,025 yüzdelik dilime karşılık gelen z-puanı -1,96’dır .

Yani aralarındaki dağılımın %95’ini oluşturan z puanları -1,96 ile 1,96’dır .

3. TI-84 hesap makinesinde invNorm() işlevini kullanın.

TI-84 hesap makinesinde invNorm() işlevi kullanıldığında, soldaki 0,025’lik alana karşılık gelen z puanı -1,96 olur.

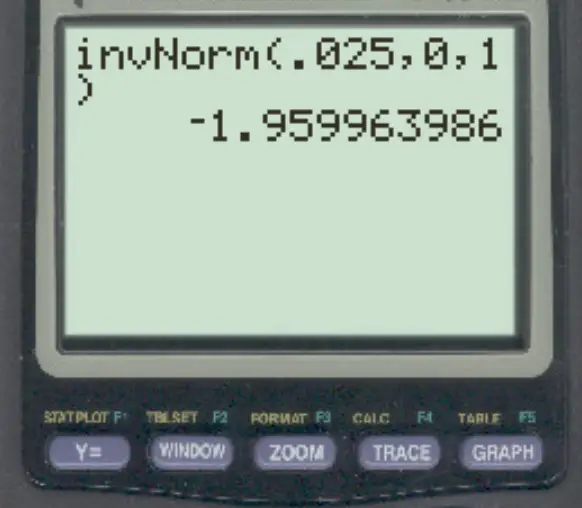
Yani aralarındaki dağılımın %95’ini oluşturan z puanları -1,96 ile 1,96’dır .