R'de veri nasıl dönüştürülür (log, kare kök, küp kök)

Birçok istatistiksel test, bir yanıt değişkeninin artıklarının normal şekilde dağıldığını varsayar.

Ancak artıklar çoğu zaman normal dağılıma sahip değildir . Bu sorunu çözmenin bir yolu, yanıt değişkenini üç dönüşümden birini kullanarak dönüştürmektir:

1. Günlük dönüşümü: yanıt değişkenini y’den log(y)’ ye dönüştürün.

2. Karekök dönüşümü: Yanıt değişkenini y’den √y’ye dönüştürün.

3. Küp kök dönüşümü: yanıt değişkenini y’den y ^1/3’e dönüştürün.

Bu dönüşümleri gerçekleştirerek, yanıt değişkeni genellikle normal dağılıma yaklaşır. Aşağıdaki örnekler bu dönüşümlerin R’de nasıl gerçekleştirileceğini göstermektedir.

R’de günlük dönüşümü

Aşağıdaki kod, bir yanıt değişkeninde günlük dönüşümünün nasıl gerçekleştirileceğini gösterir:

 #create data frame
df <- data.frame(y=c(1, 1, 1, 2, 2, 2, 2, 2, 2, 3, 3, 3, 6, 7, 8),
                 x1=c(7, 7, 8, 3, 2, 4, 4, 6, 6, 7, 5, 3, 3, 5, 8),
                 x2=c(3, 3, 6, 6, 8, 9, 9, 8, 8, 7, 4, 3, 3, 2, 7))

#perform log transformation
log_y <- log10(df$y)

Aşağıdaki kod, bir log dönüşümü gerçekleştirmeden önce ve sonra y dağılımını görüntülemek için histogramların nasıl oluşturulacağını gösterir:

 #create histogram for original distribution
hist(df$y, col='steelblue', main='Original')

#create histogram for log-transformed distribution 
hist(log_y, col='coral2', main='Log Transformed')

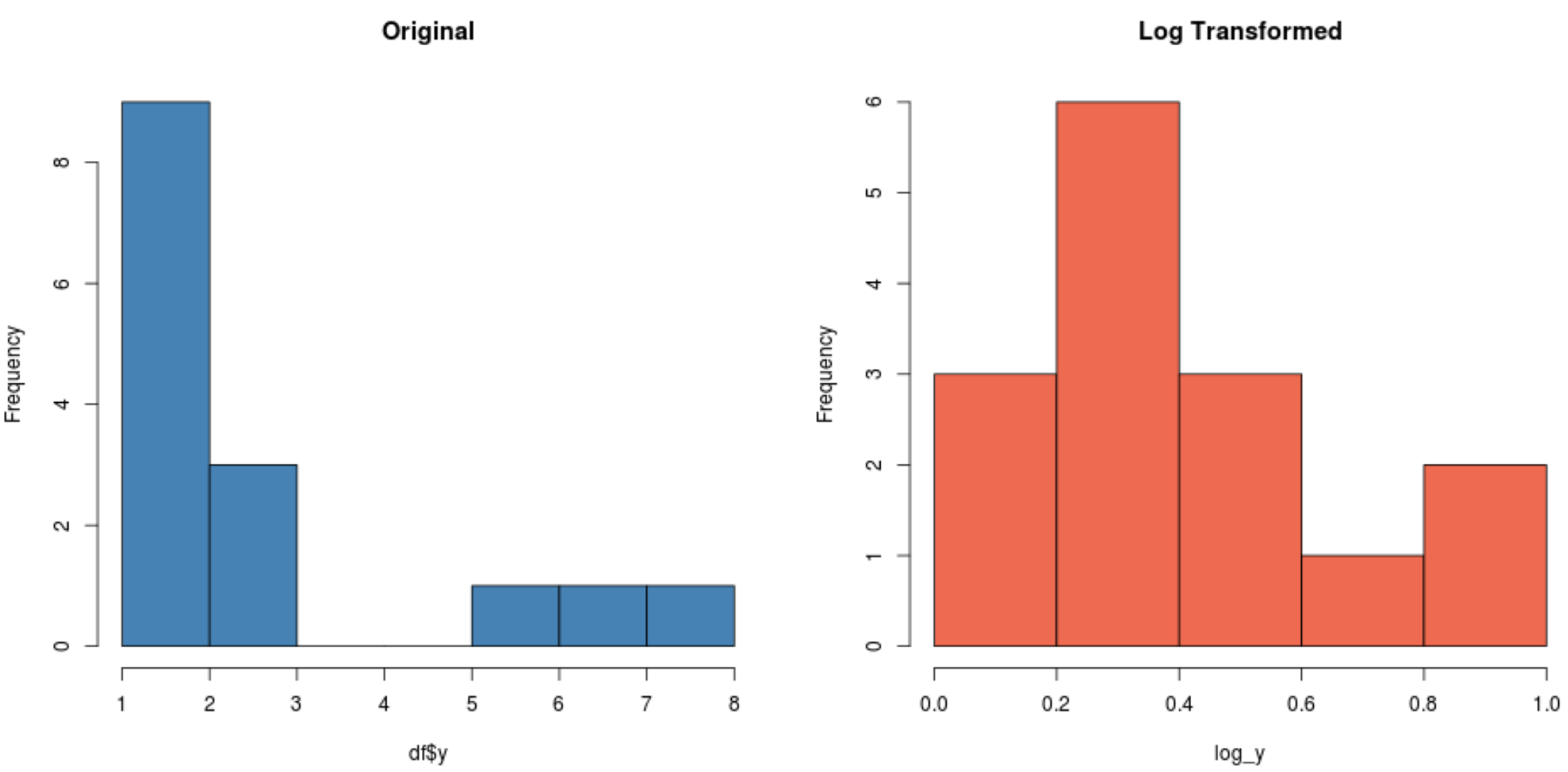
Log-dönüştürülmüş dağılımın orijinal dağılımdan çok daha normal olduğuna dikkat edin. Hala mükemmel bir “çan şekli” değil ama normal dağılıma orijinal dağılımdan daha yakın.

Aslında, her dağılıma birShapiro-Wilk testi uygularsak, orijinal dağılımın normallik varsayımını karşılayamadığını, log-dönüştürülmüş dağılımın ise başaramadığını görürüz (α = 0,05’te):

 #perform Shapiro-Wilk Test on original data
shapiro.test(df$y)

	Shapiro-Wilk normality test

data: df$y
W = 0.77225, p-value = 0.001655

#perform Shapiro-Wilk Test on log-transformed data 
shapiro.test(log_y)

	Shapiro-Wilk normality test

data:log_y
W = 0.89089, p-value = 0.06917

R’de karekök dönüşümü

Aşağıdaki kod, bir yanıt değişkeninde karekök dönüşümünün nasıl gerçekleştirileceğini gösterir:

 #create data frame
df <- data.frame(y=c(1, 1, 1, 2, 2, 2, 2, 2, 2, 3, 3, 3, 6, 7, 8),
                 x1=c(7, 7, 8, 3, 2, 4, 4, 6, 6, 7, 5, 3, 3, 5, 8),
                 x2=c(3, 3, 6, 6, 8, 9, 9, 8, 8, 7, 4, 3, 3, 2, 7))

#perform square root transformation
sqrt_y <- sqrt(df$y)

Aşağıdaki kod, karekök dönüşümü gerçekleştirmeden önce ve sonra y dağılımını görüntülemek için histogramların nasıl oluşturulacağını gösterir:

 #create histogram for original distribution
hist(df$y, col='steelblue', main='Original')

#create histogram for square root-transformed distribution 
hist(sqrt_y, col='coral2', main='Square Root Transformed') 

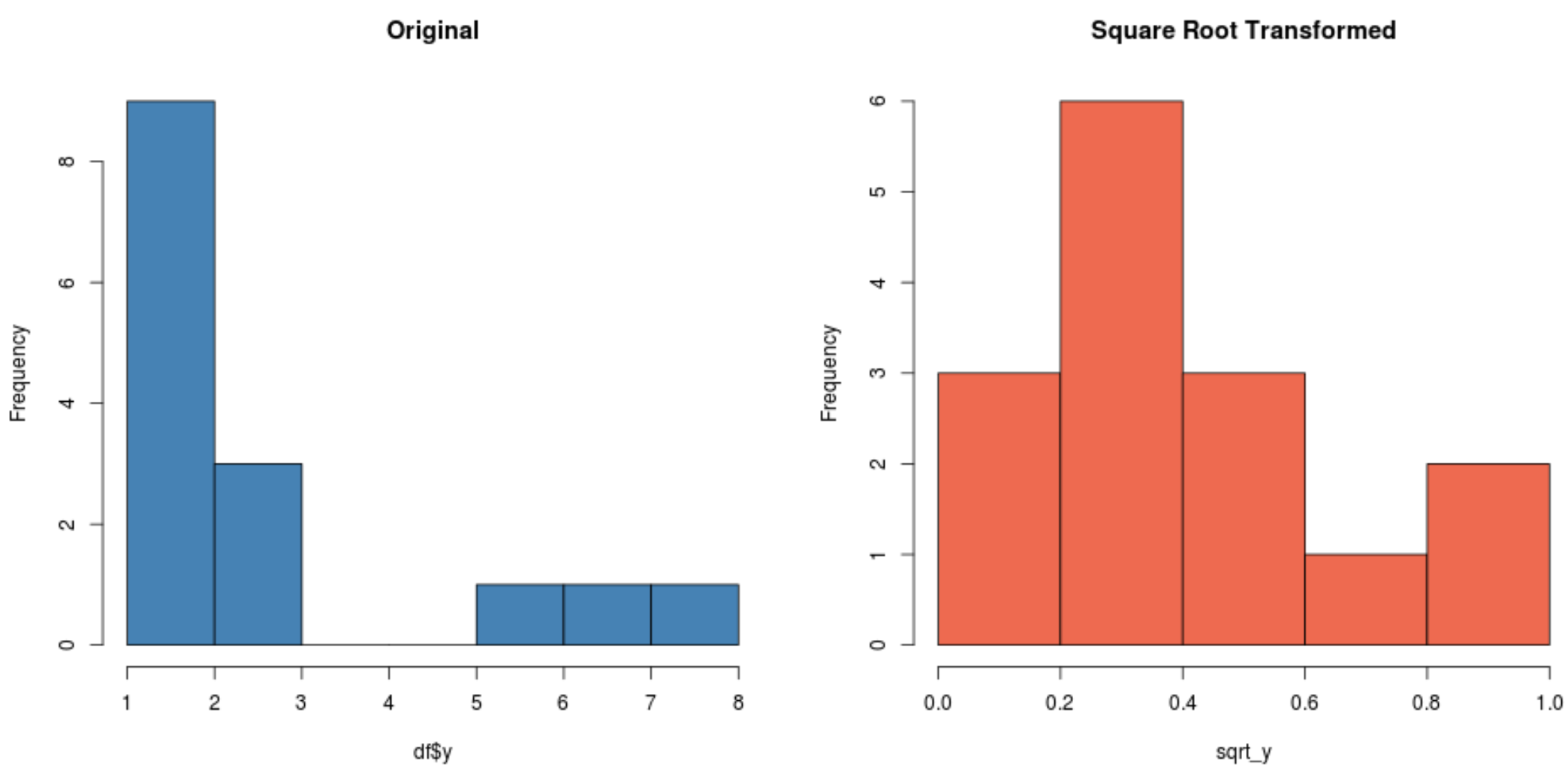
Karekök dönüştürülmüş dağılımın orijinal dağılımdan çok daha normal dağıldığına dikkat edin.

R’de küp kök dönüşümü

Aşağıdaki kod, bir yanıt değişkeninde küp kök dönüşümünün nasıl gerçekleştirileceğini gösterir:

 #create data frame
df <- data.frame(y=c(1, 1, 1, 2, 2, 2, 2, 2, 2, 3, 3, 3, 6, 7, 8),
                 x1=c(7, 7, 8, 3, 2, 4, 4, 6, 6, 7, 5, 3, 3, 5, 8),
                 x2=c(3, 3, 6, 6, 8, 9, 9, 8, 8, 7, 4, 3, 3, 2, 7))

#perform square root transformation
cube_y <- df$y^(1/3)

Aşağıdaki kod, karekök dönüşümü gerçekleştirmeden önce ve sonra y dağılımını görüntülemek için histogramların nasıl oluşturulacağını gösterir:

 #create histogram for original distribution
hist(df$y, col='steelblue', main='Original')

#create histogram for square root-transformed distribution 
hist(cube_y, col='coral2', main='Cube Root Transformed') 

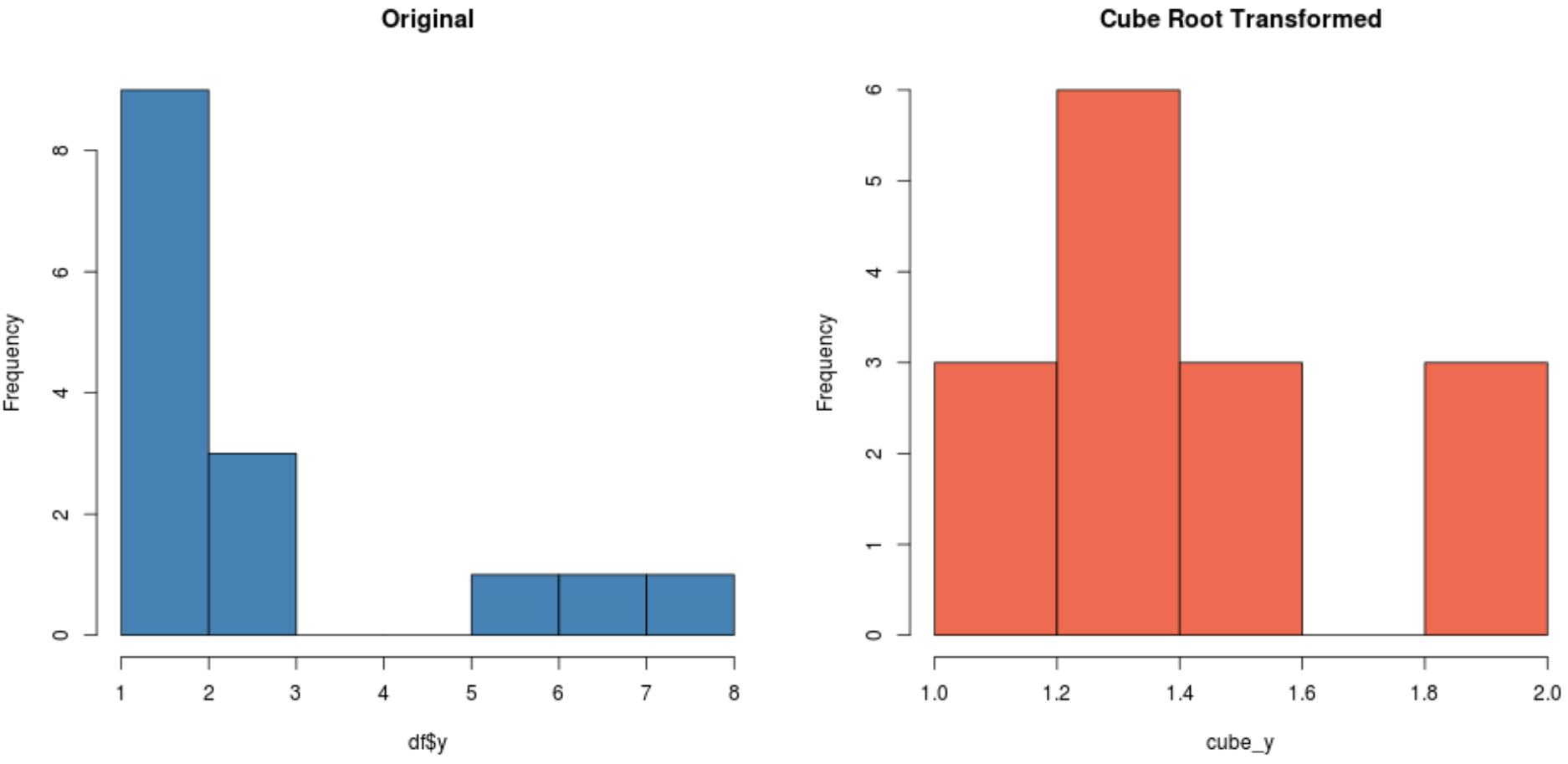
Veri kümenize bağlı olarak bu dönüşümlerden biri, diğerlerinden daha normal şekilde dağıtılan yeni bir veri kümesi üretebilir.