Yarı standart sapma

İle Dr.benjamin anderson Ağustos 3, 2023 İstatistik 0 Yorum

Bu makalede istatistikte yarı standart sapmanın ne olduğu ve nasıl hesaplandığı açıklanmaktadır. Böylece yarı standart sapma formülünü, çözülmüş bir alıştırmayı ve ek olarak herhangi bir veri kümesinin yarı standart sapmasını hesaplamak için çevrimiçi bir hesap makinesi bulacaksınız.

Yarı standart sapma nedir?

İstatistikte yarı standart sapma , numunenin değişkenliğini gösteren bir dağılım ölçüsüdür. Spesifik olarak, yarı standart sapma, sapmaların karelerinin toplamının karekökünün, toplam veri noktası sayısı eksi bire bölünmesine eşittir.

Yarı standart sapmanın sembolü σ _n-1 veya _n-1’dir .

Yarı standart sapma aynı zamanda yarı standart sapma olarak da adlandırılabilir ve bazen örnek standart sapma olarak da adlandırılır, çünkü genellikle istatistiksel bir örnekten alınan değerler kullanılarak hesaplanır. Aşağıda yarı standart sapma ile standart sapma arasındaki fark hakkında ayrıntılı bilgi vereceğiz.

Yarı standart sapma formülü

Yarı standart sapma, veri serisindeki sapmaların karelerinin toplamının karekökünün toplam gözlem sayısı eksi bire bölünmesine eşittir. Bu nedenle, yarı standart sapmayı hesaplama formülü şöyledir:

Altın:

$\sigma_{n-1}$

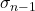
Bu yarı standart sapmadır.
$x_i$

veri değeri

$i$

.
$n$

toplam veri sayısıdır.
$\overline{x}$

veri setinin ortalamasıdır.

👉Herhangi bir veri seti için yarı standart sapmayı hesaplamak için aşağıdaki hesaplayıcıyı kullanabilirsiniz.

Yarı standart sapmayı hesaplama örneği

Yarı standart sapmanın tanımı göz önüne alındığında, aşağıda bir veri setinin yarı standart sapmasının nasıl hesaplanacağına dair basit bir örnek görebilirsiniz.

Bir şirketin araştırma ve geliştirme departmanına ayırdığı bütçe, şirketin önceki yılda elde ettiği ekonomik kâra bağlı olduğundan çok değişkendir. Böylece son beş yılda bu kesimin bütçesi şöyle oldu: 3, 6, 2, 9, 4 milyon euro. Bu veri serisinin yarı standart sapmasını hesaplayın.

Yarı standart sapmayı belirlemek için yapmamız gereken ilk şey, örneğin aritmetik ortalamasını hesaplamaktır. Bunu yapmak için tüm verileri toplayıp toplam gözlem sayısına bölüyoruz ki bu da beştir:

$\overline{x}=\cfrac{3+6+2+9+4}{5}=4,8$

Daha sonra yarı standart sapma formülünü uyguluyoruz:

$\displaystyle\sigma_{n-1}=\sqrt{\frac{\displaystyle\sum_{i=1}^n(x_i-\overline{x})^2}{n-1}}$

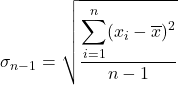
Verileri formülde değiştiririz:

$\displaystyle \sigma_{n-1}=\sqrt{\frac{(3-4,8)^2+(6-4,8)^2+(2-4,8)^2+(9-4,8)^2+(4-4,8)^2}{5-1}}$

Ve son olarak yarı standart sapmayı hesaplıyoruz:

$\begin{aligned}\displaystyle\sigma_{n-1} & = \sqrt{\frac{(-1,8)^2+1,2^2+(-2,8)^2+4,2^2+(-0,8)^2}{5-1}}\\[2ex]&=\sqrt{\frac{3,24+1,44+7,84+17,64+0,64}{4}}\\[2ex]&= \sqrt{\frac{30,8}{4}}=\sqrt{7,7}=2,77 \end{aligned}$

Kısacası veri örneğinin yarı standart sapması 2,77 milyondur.

➤ Bakınız: Yarı-varyans

Yarı standart sapma hesaplayıcısı

Yarı standart sapmasını hesaplamak için bir istatistiksel veri setini aşağıdaki çevrimiçi hesap makinesine takın. Veriler bir boşlukla ayrılmalı ve ondalık ayırıcı olarak nokta kullanılarak girilmelidir.

Yarı standart sapma ve standart sapma

Son olarak yarı standart sapma ile standart sapma arasındaki farkın ne olduğunu göreceğiz çünkü bunlar çok benzer ada sahip ve çok benzer şekilde hesaplanan iki farklı istatistiksel ölçüdür.

Yarı standart sapma ile standart sapma arasındaki fark formülün paydasıdır. Yarı standart sapmayı hesaplamak için n-1’e bölün, ancak standart sapma n’ye bölünerek hesaplanır.

Bu nedenle yarı standart sapma ve standart sapma matematiksel olarak ilişkilidir, çünkü yarı standart sapma standart sapma çarpı n’nin (toplam veri noktası sayısı) n-1’in kareköküne eşittir.

$\displaystyle\sigma_{n-1}=\sqrt{\frac{n}{n-1}}\cdot \sigma$

Önceki denklemden, aynı veri seti için yarı standart sapma değerinin her zaman standart sapma değerinden daha büyük olacağı sonucunu çıkarabiliriz.

Ek olarak, yarı standart sapma formülü, önyargıyı ortadan kaldırdığı için bir numunenin standart sapmasını hesaplamak için sıklıkla kullanılır. Bu nedenle yarı standart sapma, popülasyon standart sapmasının iyi bir tahmincisidir. Bu nedenle, bir örnekten istatistiksel çıkarım yaparken standart sapmanın hesaplandığını söylemek oldukça yaygındır, ancak gerçekte hesaplanan yarı standart sapmadır.

➤ Bakınız: Standart sapmanın özellikleri

yazar hakkında

Dr.benjamin anderson

Merhaba, ben Benjamin, emekli bir istatistik profesörü ve Statorials öğretmenine dönüştüm. İstatistik alanındaki kapsamlı deneyimim ve uzmanlığımla, öğrencilerimi Statorials aracılığıyla güçlendirmek için bilgilerimi paylaşmaya can atıyorum. Daha fazlasını bil