Yarı-varyans

İle Dr.benjamin anderson Ağustos 3, 2023 İstatistik 0 Yorum

Bu makale istatistikte yarı-varyansın ne olduğunu açıklamaktadır. Böylece, quasivariance’ın nasıl hesaplanacağını, çözülmüş bir alıştırmayı ve quasivariance ile varyans arasındaki farkların neler olduğunu keşfedeceksiniz. Ek olarak, çevrimiçi bir hesap makinesiyle herhangi bir veri kümesinin yarı-varyansını hesaplayabilirsiniz.

Yarı değişkenlik nedir?

İstatistikte yarı değişkenlik , bir numunenin değişkenliğini gösteren bir dağılım ölçüsüdür. Daha kesin olarak yarı değişkenlik, sapmaların karelerinin toplamının toplam gözlem sayısına bölünerek bir eksiğine eşittir.

Yarı-değişkenlik sembolü

$\sigma_{n-1}^2$

herhangi biri

$s_{n-1}^2$

. Bazen sembol de kullanılsa da

$\widehat{s}^2$

yarı-varyansı temsil etmek için.

Yarı değişkenlik, önyargıdan kaçınarak bir numunenin dağılımını belirlemek için kullanılır; bu nedenle buna genellikle tarafsız varyans denir. Dolayısıyla quasivariance popülasyon varyansının iyi bir tahmincisidir. Aslında örneklem varyansını hesaplarken varyans formülü yerine sıklıkla yarı varyans formülü kullanılır. Aşağıda bu iki istatistiksel ölçüm arasındaki fark hakkında ayrıntılı bilgi vereceğiz.

Yarı varyans formülü

Yarı-varyansı hesaplamak için, değerler ile veri kümesinin ortalaması arasındaki farkların karelerinin toplamını bulmak ve daha sonra bunu toplam veri sayısından bir eksiğine bölmek gerekir.

Dolayısıyla yarı-varyansı hesaplamak için kullanılan formül aşağıdaki gibidir:

Altın:

$\sigma_{n-1}^2$

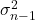
yarı-varyanstır.
$x_i$

veri değeri

$i$

.
$n$

toplam veri sayısıdır.
$\overline{X}$

veri setinin ortalamasıdır.

👉 Herhangi bir veri setinin yarı varyansını hesaplamak için aşağıdaki hesaplayıcıyı kullanabilirsiniz.

Neden n’ye değil de n-1’e bölündüğünü merak ediyor olabilirsiniz? Bu önyargıyı ortadan kaldırmakla ilgili, bu şekilde tarafsız bir tahminci elde ediyoruz. Yarı-değişkenliğin popülasyon varyansının iyi bir tahmincisi olmasının nedeni tam olarak budur.

Yarı değişkenlik hesaplama örneği

Artık yarı değişkenliğin tanımını bildiğimize göre, bir veri serisinin yarı değişkenliğinin nasıl hesaplandığını görebilmeniz için basit bir örnek çözeceğiz.

Çok uluslu bir şirketten, son beş yılda elde ettiği ekonomik sonucu biliyoruz, çoğunluğu kar elde etti ama bir yıl ciddi zararlar verdi: 11,5, 2, -9, 7 milyon euro. Bu veri setinin yarı-varyansını hesaplayın.

Bir veri setinin yarı-varyansını elde etmek için yapmamız gereken ilk şey aritmetik ortalamasını hesaplamaktır:

$\overline{X}=\cfrac{11+5+2+(-9)+7}{5}=3,2$

Verilerin ortalama değerini bildiğimizde yarı-varyans formülünü uygularız:

$\sigma_{n-1}^2=\cfrac{\displaystyle\sum_{i=1}^n\left(x_i-\overline{X}\right)^2}{n-1}$

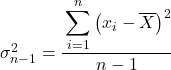
Bu nedenle, egzersiz talimatının sağladığı verileri formülde değiştiriyoruz:

$\sigma_{n-1}^2=\cfrac{\displaystyle (11-3,2)^2+(5-3,2)^2+(2-3,2)^2+(-9-3,2)^2+(7-3,2)^2}{5-1}$

Son olarak, yarı-varyansı hesaplamak için işlemleri çözmek yeterlidir:

$\begin{aligned}\sigma_{n-1}^2&=\cfrac{7,8^2+1,8^2+(-1,2)^2+(-12,2)^2+3,8^2}{5}\\[2ex]&=\cfrac{60,84+3,24+1,44+148,84+14,44}{5-1}\\[2ex]&= \cfrac{228,8}{4} \\[2ex]&=57,2 \ \text{millones de euros}^2\end{aligned}$

Yarı-değişkenlik birimlerinin istatistiksel veri birimleriyle aynı birimler olduğunu ancak kareleri olduğunu unutmayın; dolayısıyla bu veri kümesinin yarı-değişkenliği 57,2 milyon ^2’dir .

➤ Bakınız: Yarı standart sapma

Yarı-varyans hesaplayıcısı

Yarı değişkenliğini hesaplamak için aşağıdaki hesap makinesine bir istatistiksel veri seti girin. Veriler bir boşlukla ayrılmalı ve ondalık ayırıcı olarak nokta kullanılarak girilmelidir.

Varyans ve yarı-varyans

Son olarak quasivariance ve varyans arasındaki farkı göreceğiz çünkü isim benzerliğine rağmen aynı zamanda çok benzer şekilde hesaplanırlar.

Yarı değişkenlik ile varyans arasındaki fark, formülün paydasıdır. Yarı değişkenliği hesaplamak için n-1’e bölmeniz gerekir, ancak varyans n’ye bölünerek hesaplanır.

Bu nedenle, yarı-değişkenlik ve varyans matematiksel olarak ilişkilidir, çünkü yarı-değişkenlik, varyansın n (toplam veri noktası sayısı) ile çarpımına ve n-1’e bölünmesine eşdeğerdir.

$\sigma_{n-1}^2=\cfrac{n}{n-1}\cdot \sigma^2$

Bu nedenle aynı veri seti için yarı-varyans değeri her zaman varyans değerinden büyük olacaktır.

➤ Bakınız: Sapmaların özellikleri

yazar hakkında

Dr.benjamin anderson

Merhaba, ben Benjamin, emekli bir istatistik profesörü ve Statorials öğretmenine dönüştüm. İstatistik alanındaki kapsamlı deneyimim ve uzmanlığımla, öğrencilerimi Statorials aracılığıyla güçlendirmek için bilgilerimi paylaşmaya can atıyorum. Daha fazlasını bil