Yoğunluk eğrileri nedir? (açıklama ve örnekler)

Yoğunluk eğrisi, bir veri kümesindeki değerlerin dağılımını temsil eden bir grafik üzerindeki eğridir. Bu üç nedenden dolayı faydalıdır:

1. Yoğunluk eğrisi bize, bir dağılımın bir veya daha fazla frekans değeri “zirvesine” sahip olup olmadığı ve dağılımın sola çarpık olup olmadığı da dahil olmak üzere, bir dağılımın “şekli” hakkında iyi bir fikir verir. veya doğru. SAĞ. .

2. Yoğunluk eğrisi, bir dağılımın ortalamasının ve medyanının nerede ilişkili olduğunu görsel olarak görmemizi sağlar.

3. Yoğunluk eğrisi, bir veri setindeki gözlemlerin yüzde kaçının farklı değerler arasında kaldığını görsel olarak görmemizi sağlar.

En iyi bilinen yoğunluk eğrisi normal dağılımı temsil eden çan şeklindeki eğridir.

Yoğunluk eğrilerini daha iyi anlamak için aşağıdaki örneği inceleyin.

Örnek: yoğunluk eğrisi oluşturma ve yorumlama

Diyelim ki belirli bir alandaki 20 farklı bitkinin boyunu (inç cinsinden) gösteren aşağıdaki veri setine sahibiz:

4, 5, 5, 6, 6, 6, 6, 7, 7, 7, 7, 7, 8, 8, 8, 9, 9, 9, 2, 2

Her değerin göreceli frekanslarını görüntülemek için basit bir histogram oluştursaydık, şuna benzerdi:

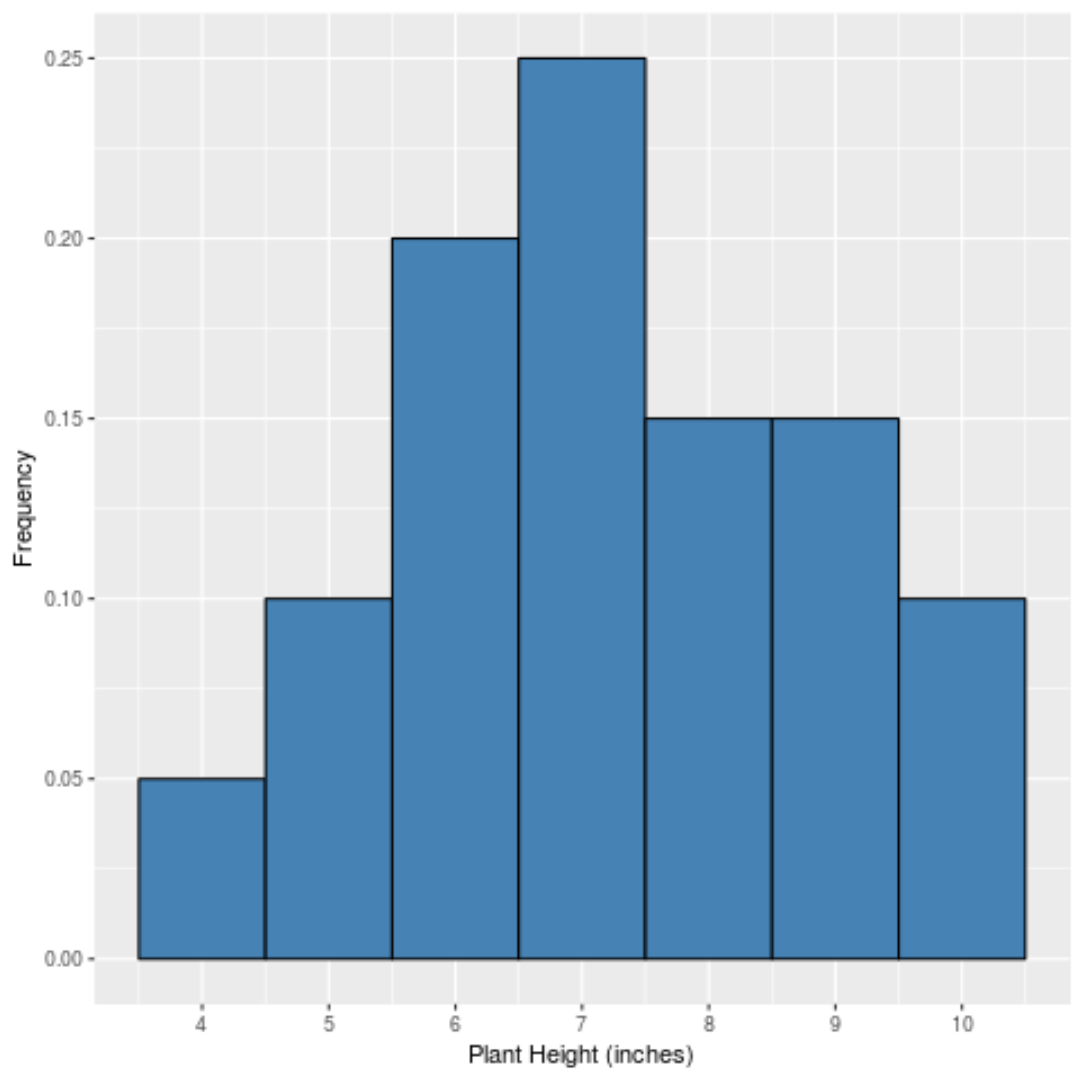
X ekseni veri değerini, y ekseni ise bağıl frekansı gösterir (örneğin, “7” değeri veri kümesindeki 20 toplam değerin 5 katı kadar görünür, yani %25 bağıl sıklığa sahiptir veya 0.25 .

Ve eğer bu dağılımın “şeklini” yakalamak için bir yoğunluk eğrisi yaratsaydık, şuna benzerdi:

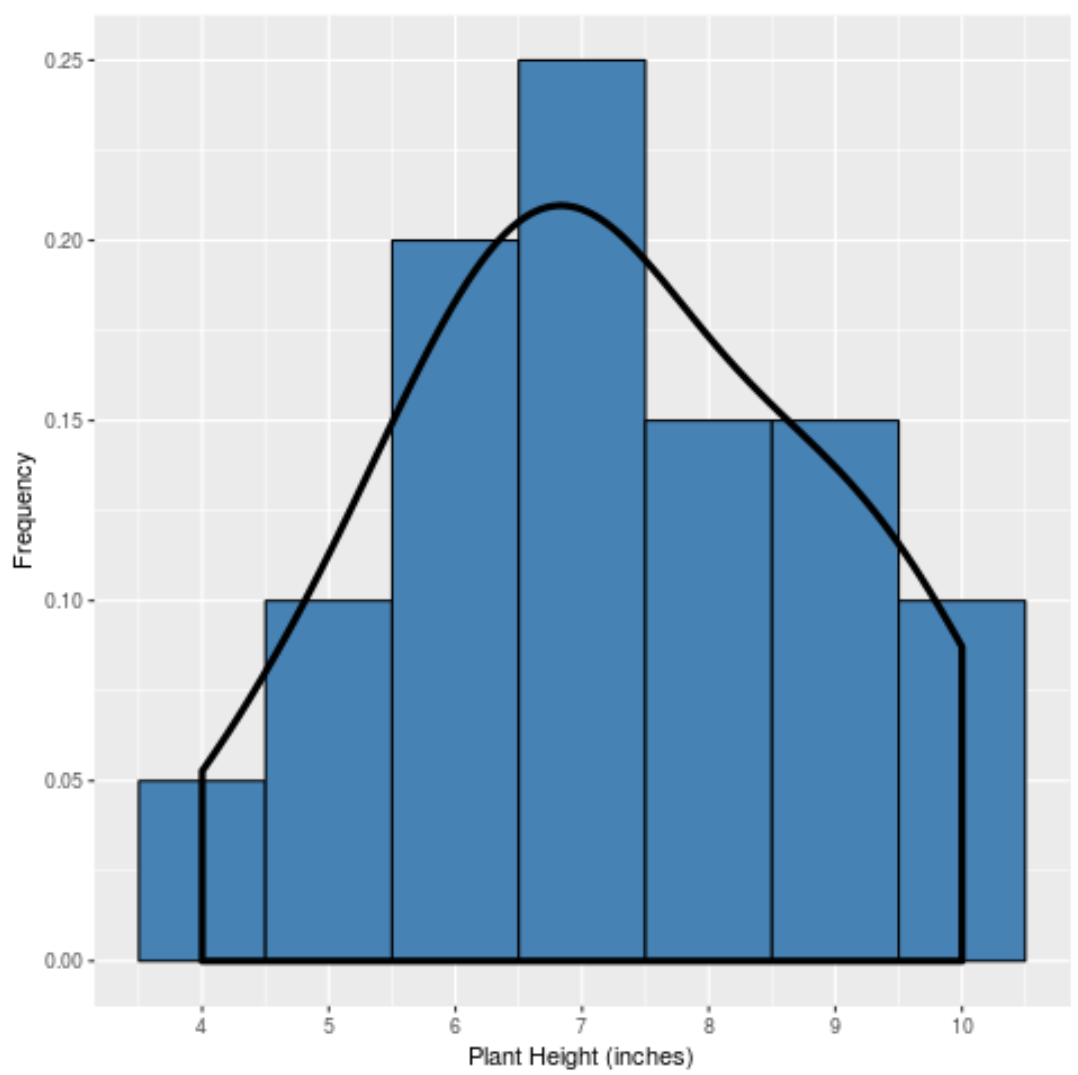
Eğri, dağılımın merkezine yakın yerde en yüksektir çünkü değerlerin çoğunun bulunduğu yer burasıdır. Aynı zamanda dağılımın uçlarına yakın yerlerde de en düşüktür çünkü daha az sayıda bitki bu değerleri alır (örneğin yükseklik 4 inç veya 10 inç).

Yoğunluk eğrileri nasıl yorumlanır?

Yoğunluk eğrileri her şekil ve boyutta olabilir ve belirli bir veri kümesindeki değerlerin dağılımını hızlı bir şekilde görsel olarak anlamamızı sağlar. Bunlar özellikle aşağıdakileri görselleştirmemize yardımcı olmak açısından faydalıdır:

1. Asimetri

Çarpıklık, bir dağılımın simetrisini tanımlamanın bir yoludur. Yoğunluk eğrileri, bir grafiğin sola mı, sağa mı eğimli olduğunu veya eğiminin olmadığını hızlı bir şekilde görmemize olanak tanır:

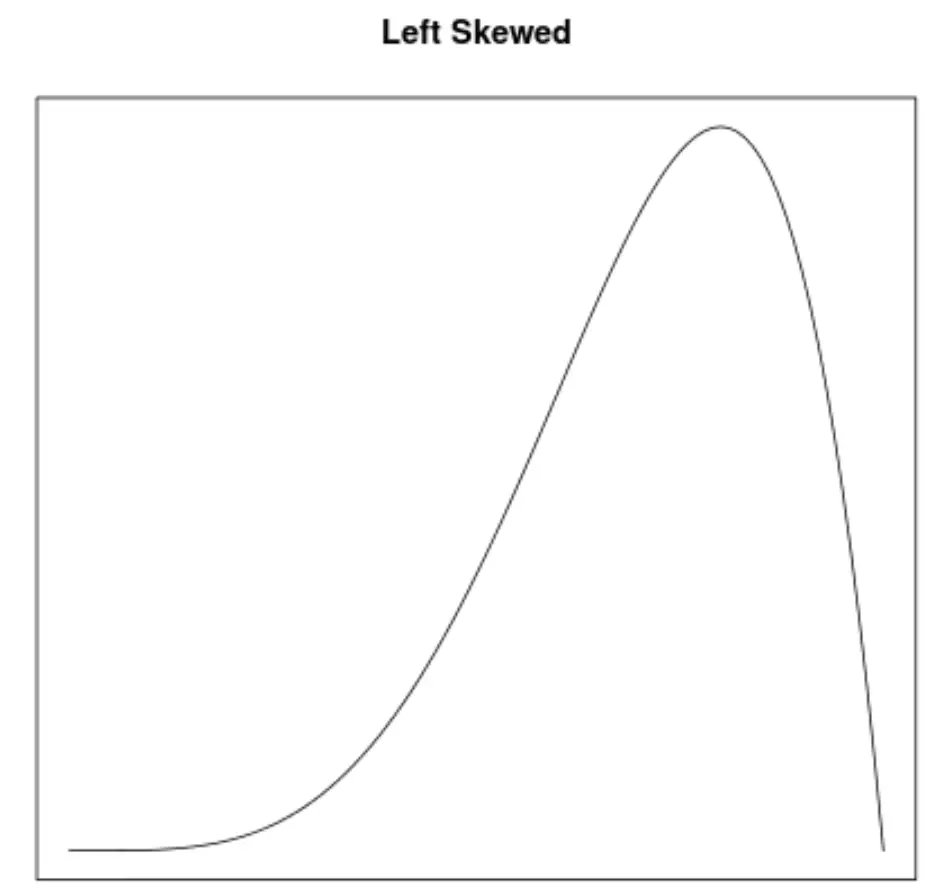
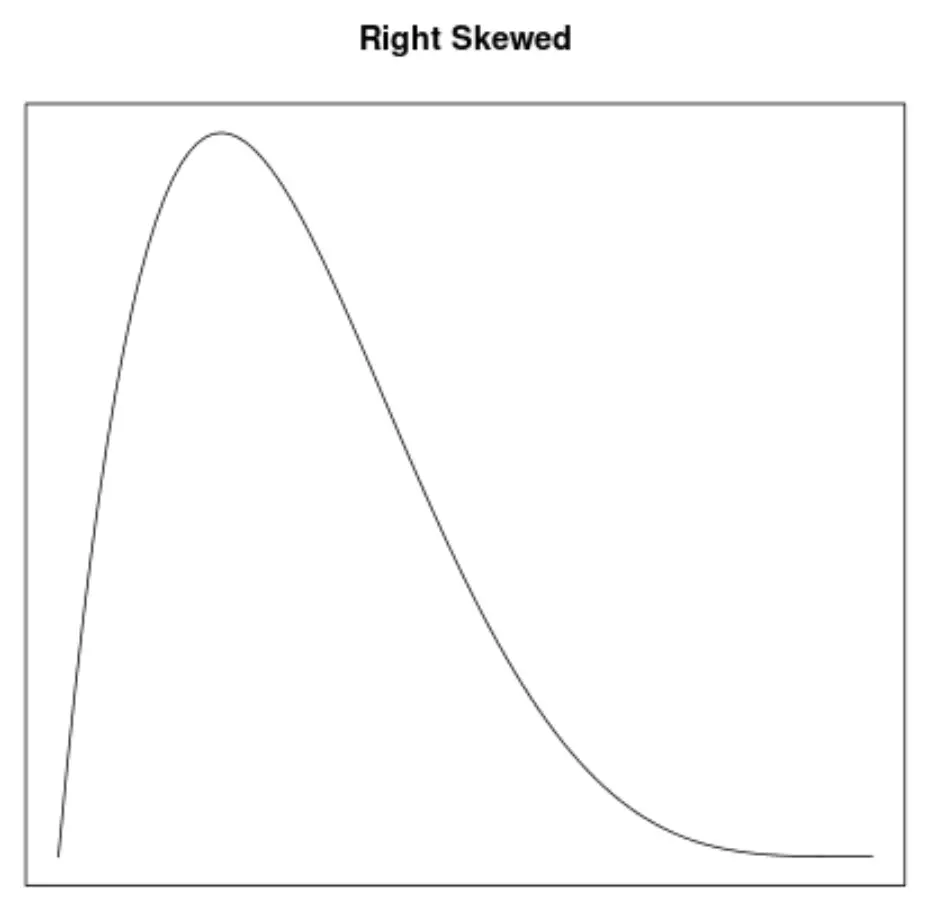
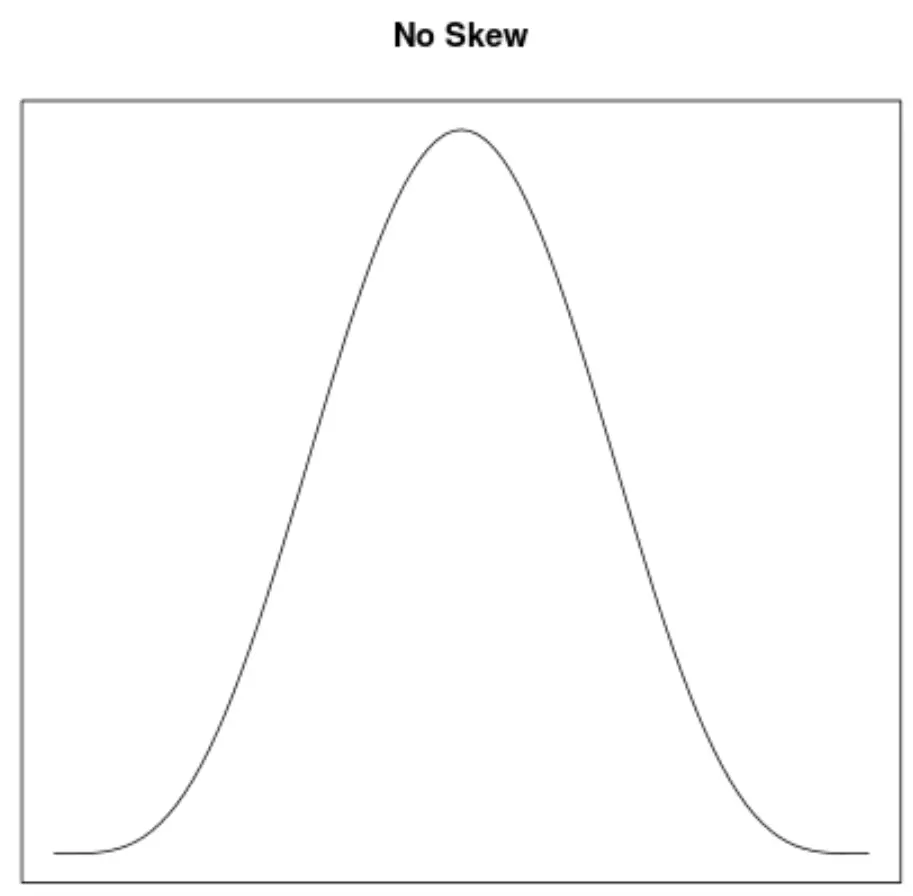
2. Ortalama ve medyanın konumu

Yoğunluk eğrisinin çarpıklığına dayanarak, belirli bir dağılımda ortalamanın mı yoksa medyanın mı daha büyük olduğunu hızlı bir şekilde söyleyebiliriz. Özellikle:

• Yoğunluk eğrisi asimetrik kalırsa , ortalama medyandan daha düşüktür .
• Yoğunluk eğrisi sağa çarpıksa ortalama ortancadan büyüktür .
• Yoğunluk eğrisinde asimetri yoksa ortalama medyana eşittir .

3. Piklerin sayısı

Yoğunluk eğrileri aynı zamanda belirli bir dağılımda kaç tane “zirve” bulunduğunu hızlı bir şekilde görmemize olanak tanır. Yukarıdaki örneklerin her birinde, dağılımların yalnızca bir zirvesi vardı, dolayısıyla bu dağılımları tek modlu olarak tanımlayabiliriz.

Ancak bazı dağılımların bimodal dağılım dediğimiz iki zirvesi olabilir. Nadir durumlarda iki veya daha fazla zirveye sahip multimodal dağılımlara da sahip olabiliriz.

Belirli bir veri seti için basitçe bir yoğunluk eğrisi oluşturarak, dağılımda kaç tane zirve olduğunu hızlı bir şekilde görebiliriz.

Yoğunluk eğrilerinin özellikleri

Yoğunluk eğrileri aşağıdaki özelliklere sahiptir:

• Eğrinin altındaki alanın toplamı her zaman %100 olur.
• Eğri hiçbir zaman x ekseninin altına inmeyecektir.

Farklı dağılımlar için yoğunluk eğrileri oluştururken veya yorumlarken bu iki gerçeği aklınızda bulundurun.

Ek kaynaklar

Göreli Frekans Histogramlarına Giriş
Excel’de Çan Eğrisi Nasıl Oluşturulur
Python’da Çan Eğrisi Nasıl Oluşturulur