Yoğunluk fonksiyonu

İle Dr.benjamin anderson Ağustos 5, 2023 Olasılık 0 Yorum

Bu makalede yoğunluk fonksiyonunun ne olduğunu, yoğunluk fonksiyonundan olasılığın nasıl hesaplandığını ve bu olasılık fonksiyonunun özelliklerini keşfedeceksiniz. Ek olarak yoğunluk fonksiyonu ile dağılım fonksiyonu arasındaki farkların ne olduğunu görebileceksiniz.

Yoğunluk fonksiyonu nedir?

Olasılık yoğunluk fonksiyonu olarak da adlandırılan yoğunluk fonksiyonu , sürekli bir rastgele değişkenin belirli bir değeri alma olasılığını açıklayan matematiksel bir fonksiyondur.

Başka bir deyişle, bir değişkene ilişkin yoğunluk fonksiyonu, değişkenin değer alma olasılıklarını matematiksel olarak tanımlar.

Örneğin, bir popülasyonda yetişkin bir kişinin 1,80 m’den uzun olma olasılığı %35 olsun, bu durumda yoğunluk fonksiyonu söz konusu olasılığı hesaplarken %35’lik bir olasılığı gösterecektir.

Bazen olasılık yoğunluk fonksiyonu PDF olarak kısaltılır.

Yoğunluk fonksiyonuyla olasılık hesaplama

Sürekli bir değişkenin bir aralıkta değer alma olasılığını bulmak için, söz konusu değişkene ilişkin yoğunluk fonksiyonunun aralığın sınırları arasındaki integralinin hesaplanması gerekir.

$\displaystyle P[a\leq X\leq b]=\int_a^b f(x)dx$

Altın

$f(x)$

sürekli rastgele değişkenin yoğunluk fonksiyonudur.

Veya diğer bir deyişle değişkenin bir aralıkta değer alma olasılığı, o aralıkta yoğunluk fonksiyonunun altında kalan alana eşittir.

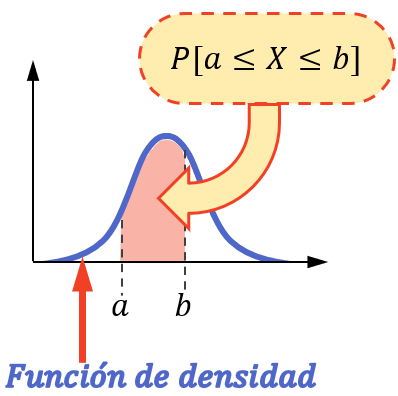
Olasılık hesaplamasının ancak istatistiksel değişkenin normal dağılım, üstel dağılım, Poisson dağılımı vb. gibi sürekli bir dağılım izlemesi durumunda bu şekilde yapılabileceğini unutmayın.

Yoğunluk fonksiyonunun özellikleri

Yoğunluk fonksiyonu aşağıdaki özelliklere sahiptir:

Yoğunluk fonksiyonunun değeri herhangi bir x değeri için sıfır veya pozitiftir.

$f(x)\geq 0$

Ayrıca yoğunluk fonksiyonunun maksimum değeri 1’e eşittir.

$f(x)\leq 1$

Aslında yoğunluk fonksiyonu grafiğinin altındaki toplam alan, tüm olasılıklar kümesine karşılık geldiğinden, değişken ne olursa olsun her zaman 1’e eşittir.

$\displaystyle \int_{-\infty}^{+\infty} f(x)dx=1$

Önceki bölümde açıklandığı gibi sürekli bir değişkenin bir aralıkta değer alma olasılığı, yoğunluk fonksiyonunun o aralıktaki integrali ile hesaplanır.

$\displaystyle P[a\leq X\leq b]=\int_a^b f(x)dx=F(b)-F(a)$

Yoğunluk fonksiyonu ve dağıtım fonksiyonu

Bu son bölümde yoğunluk fonksiyonu ile dağılım fonksiyonunun ne kadar farklı olduğunu göreceğiz çünkü bunlar genellikle karıştırılan iki tür olasılıksal fonksiyondur.

Matematiksel olarak dağılım fonksiyonu yoğunluk fonksiyonunun integraline eşdeğerdir , dolayısıyla dağılım fonksiyonu sürekli bir değişkenin kümülatif olasılığını tanımlar.

Yani herhangi bir değere ait dağılım fonksiyonunun görüntüsü, değişkenin o değeri veya daha düşük bir değeri alma olasılığına eşittir.

Dolayısıyla bu iki fonksiyon türü arasındaki matematiksel ilişki aşağıdaki gibidir:

$\displaystyle P[X\leq a]=\int_{-\infty}^a f(x)dx=F(a)$

Altın

$f(x)$

yoğunluk fonksiyonudur ve

$F(x)$

dağıtım fonksiyonudur.

Yoğunluk fonksiyonunun grafiksel gösteriminin, ortalaması 1 ve standart sapması 0,5 olan normal bir dağılım izleyen bir değişkenin dağılım fonksiyonuna göre nasıl değiştiğine dikkat edin:

dağıtım fonksiyonu ile yoğunluk fonksiyonu arasındaki fark

Dağıtım özelliği hakkında daha fazla bilgi edinmek için aşağıdaki bağlantıya tıklayın:

➤ Bakınız: dağıtım fonksiyonu

yazar hakkında

Dr.benjamin anderson

Merhaba, ben Benjamin, emekli bir istatistik profesörü ve Statorials öğretmenine dönüştüm. İstatistik alanındaki kapsamlı deneyimim ve uzmanlığımla, öğrencilerimi Statorials aracılığıyla güçlendirmek için bilgilerimi paylaşmaya can atıyorum. Daha fazlasını bil