Yüzdelik, çeyreklik ve niceliksel: fark nedir?

Öğrencilerin istatistikte sıklıkla karıştırdığı üç terim yüzdelik dilimler, çeyreklikler ve yüzdelik dilimlerdir.

İşte her birinin basit bir tanımı:

Yüzdelikler: 0 ile 100 arasında değişir.

Çeyrekler: 0 ile 4 arasında değişir.

Nicelikler: herhangi bir değerden başka bir değere gidin.

Yüzdelik dilimlerin ve çeyreklik dilimlerin yalnızca yüzdelik dilim türleri olduğunu unutmayın.

Bazı nicelik türlerinin belirli adları bile vardır:

• 4 niceliğe çeyrekler denir.
• 5 yüzdelik dilime beşte birlik dilimler denir.
• 8 niceliğe oktil denir.
• 10 niceliğe ondalık dilimler denir.
• 100 yüzdelik dilime yüzdelik dilimler denir.

Yüzdelikler ve çeyrekliklerin aşağıdaki ilişkiyi paylaştığını unutmayın:

• 0 yüzdelik dilim = 0 çeyreklik (minimum da denir)
• 25. yüzdelik dilim = 1. çeyrek
• 50. yüzdelik dilim = 2. çeyrek (ortanca da denir)
• 75. yüzdelik dilim = 3. çeyrek
• 100. yüzdelik dilim = 4. çeyrek (maksimum olarak da adlandırılır)

Örnek: Yüzdelik ve çeyreklik değerleri bulma

20 değere sahip aşağıdaki veri kümesine sahip olduğumuzu varsayalım:

İstatistiksel yazılımlar (Excel, R, Python vb. gibi) kullanarak bu veri seti için aşağıdaki yüzdelik dilimleri ve çeyrekleri bulabiliriz:

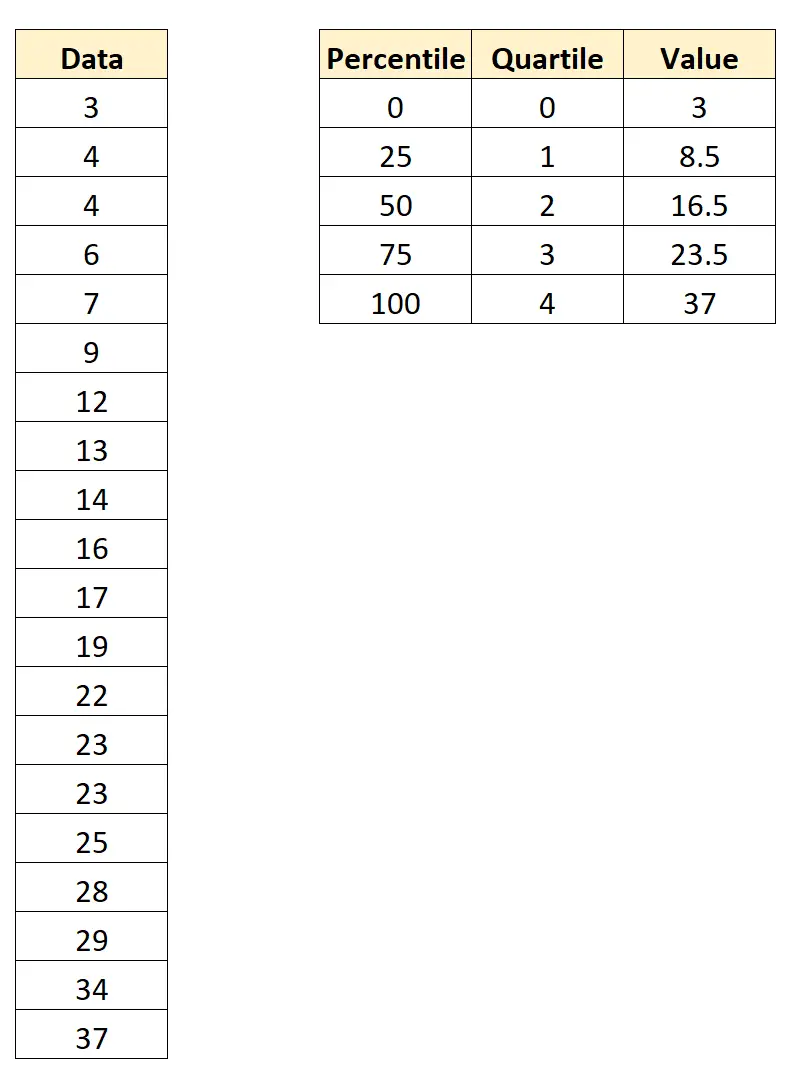
Bu değerleri nasıl yorumlayacağınız aşağıda açıklanmıştır:

• Yüzdelik 0 ve çeyreklik 0 3’tür .
• 25. yüzdelik dilim ve 1. çeyrek 8,5’tir .
• 50. yüzdelik dilim ve 2. çeyrek 16,5’tir .
• 75. yüzdelik dilim ve 3. çeyrek 23,5’tir .
• 100. yüzdelik dilim ve 4. çeyrek 37’dir .

Yüzdelik dilimler ve çeyreklikler ne zaman kullanılır?

Yüzdelikler aşağıdaki gibi soruları yanıtlamak için kullanılabilir:

Bir öğrencinin ilk %10’a girebilmesi için belirli bir testten ne kadar puan alması gerekir?

Bu soruyu cevaplamak için tüm puanların 90’ıncı yüzdelik dilimini bulmamız gerekir; bu, en alttaki %90’ı en üstteki %10’dan ayıran değerdir.

Belirli bir okuldaki öğrencilerin ortalama boylarının %40’ını hangi boylar kapsıyor?

Bu soruyu cevaplamak için boyların orta %40’ının üst ve alt sınırlarını belirleyen iki değer olan boyların 70’inci yüzdelik dilimini ve boyların 30’uncu yüzdelik dilimini bulacağız.

Çeyrekler aşağıdaki gibi soruları yanıtlamak için kullanılabilir:

Bir öğrencinin bir sınavda en üst çeyrekte yer alması için ne kadar puan alması gerekir?

Bu soruyu cevaplamak için tüm puanların 3. çeyreğini bulmamız gerekir; bu, en alttaki %75’i en üstteki %25’ten ayıran değerdir.

Belirli bir veri kümesinin çeyrekler arası aralığı nedir?

Çeyrekler arası aralık (IQR), veri değerlerinin ortadaki %50’lik aralığıdır. Belirli bir veri kümesinin IQR’sini bulmak için 3. çeyreği, yani 1. çeyreği hesaplayabiliriz.

Ek kaynaklar

R’de yüzdelikler nasıl hesaplanır
R’de çeyrekler nasıl hesaplanır
Excel’de Çeyrekler Arası Aralık Nasıl Hesaplanır?
TI-84 Hesap Makinesinde Çeyrekler Arası Aralık Nasıl Hesaplanır?