Z tablosu nasıl kullanılır (örneklerle)

Z tablosu, standart normal dağılımda değerlerin yüzde kaçının belirli bir z puanının altına düştüğünü söyleyen bir tablodur.

Z-puanı, tek bir veri değerinin ortalamadan ne kadar standart sapma düştüğünü gösterir. Aşağıdaki şekilde hesaplanır:

z-puanı = (x – μ) / σ

Altın:

• x: bireysel veri değeri
• μ: nüfus ortalaması
• σ: popülasyon standart sapması

Bu eğitimde z tablosunun kullanımına ilişkin birkaç örnek gösterilmektedir.

örnek 1

Belirli bir üniversiteye giriş sınavındaki puanlar, ortalama μ = 82 ve standart sapma σ = 8 ile normal olarak dağıtılır. Öğrencilerin yaklaşık yüzde kaçı sınavda 84’ün altında puan alıyor?

Adım 1: Z-puanını bulun.

İlk olarak, 84 sınav puanıyla ilişkili z-puanını bulacağız:

z-puanı = (x – μ) / σ = (84 – 82) / 8 = 2/8 = 0,25

Adım 2: Z puanına karşılık gelen yüzdeyi bulmak için z grafiğini kullanın.

Daha sonra z tablosunda 0,25 değerini arayacağız:

Öğrencilerin yaklaşık %59,87’si bu sınavda 84’ün altında puan alıyor.

Örnek 2

Belirli bir bahçedeki bitkilerin boyu, ortalama μ = 26,5 inç ve standart sapma σ = 2,5 inç olacak şekilde normal olarak dağılır. Bitkilerin yaklaşık yüzde kaçı 26 inçten uzun?

Adım 1: Z-puanını bulun.

İlk olarak 26 inç yüksekliğe ilişkin z-puanını bulacağız.

z-puanı = (x – μ) / σ = (26 – 26,5) / 2,5 = -0,5 / 2,5 = -0,2

Adım 2: Z puanına karşılık gelen yüzdeyi bulmak için z grafiğini kullanın.

Daha sonra -0,2 değerini arayacağız   z tablosunda:

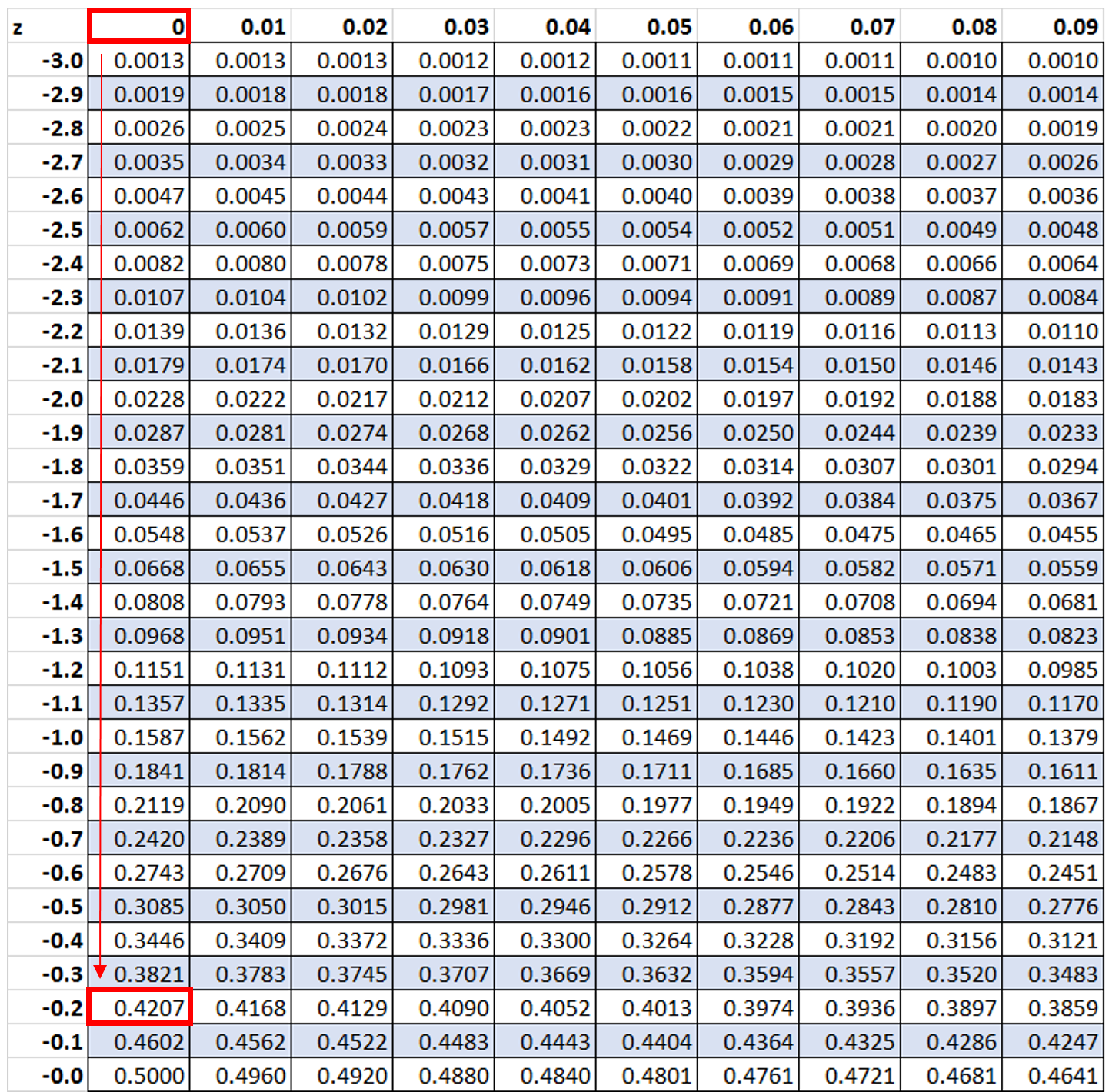
Değerlerin %42,07’sinin -0,2 z-puanının altında olduğunu görüyoruz. Ancak bu örnekte, %100 – %42,07 = %57,93 formülünü kullanarak bulabileceğimiz değerlerin yüzde kaçının -0,2’den büyük olduğunu bilmek istiyoruz.

Yani bu bahçedeki bitkilerin yaklaşık %59,87’si 26 inçten uzundur.

Örnek 3

Belirli bir yunus türünün ağırlığı, μ = 400 pound ortalaması ve σ = 25 pound standart sapması ile normal olarak dağılır. Yunusların yaklaşık yüzde kaçı 410 ila 425 pound arasındadır?

Adım 1: Z-puanlarını bulun.

İlk olarak 410 kitap ve 425 kitapla ilişkili z puanlarını bulacağız.

410’un z-puanı = (x – μ) / σ = (410 – 400) / 25 = 10/25 = 0,4

425 z puanı = (x – μ) / σ = (425 – 400) / 25 = 25 / 25 = 1

Adım 2: Her bir z puanına karşılık gelen yüzdeleri bulmak için z grafiğini kullanın.

İlk önce 0,4 değerini arayacağız.   z tablosunda:

Daha sonra 1 değerini arayacağız   z tablosunda:

Son olarak en büyük değerden en küçük değeri çıkaracağız: 0,8413 – 0,6554 = 0,1859 .

Yani yunusların yaklaşık %18,59’unun ağırlığı 410 ila 425 pound arasındadır.

Ek kaynaklar

Normal dağılıma giriş
Normal Dağıtım Alanı Hesaplayıcısı
Z puanı hesaplayıcı