İki oranlı z testi: tanım, formül ve örnek

İki popülasyon oranı arasındaki farkı test etmek için iki oranlı bir z testi kullanılır.

Bu eğitimde aşağıdakiler açıklanmaktadır:

• İki oranlı z testi gerçekleştirme motivasyonu.
• İki oranlı z testi gerçekleştirme formülü.
• İki oranlı z testinin nasıl gerçekleştirileceğine bir örnek.

İki oranlı Z testi: motivasyon

A İlçesinde belirli bir yasayı destekleyen sakinlerin oranı ile B İlçesinde yasayı destekleyen sakinlerin oranı arasında bir fark olup olmadığını bilmek istediğimizi varsayalım.

Her ilçede binlerce sakin bulunduğundan, her ilçede her bir sakini araştırmak ve araştırmak çok zaman alıcı ve pahalı olacaktır.

Bunun yerine, her ilçede yaşayanlardan basit rastgele bir örnek alabilir ve iki ilçe arasındaki oranlar arasındaki gerçek farkı tahmin etmek için her örnekte yasanın lehine olan oranı kullanabiliriz:

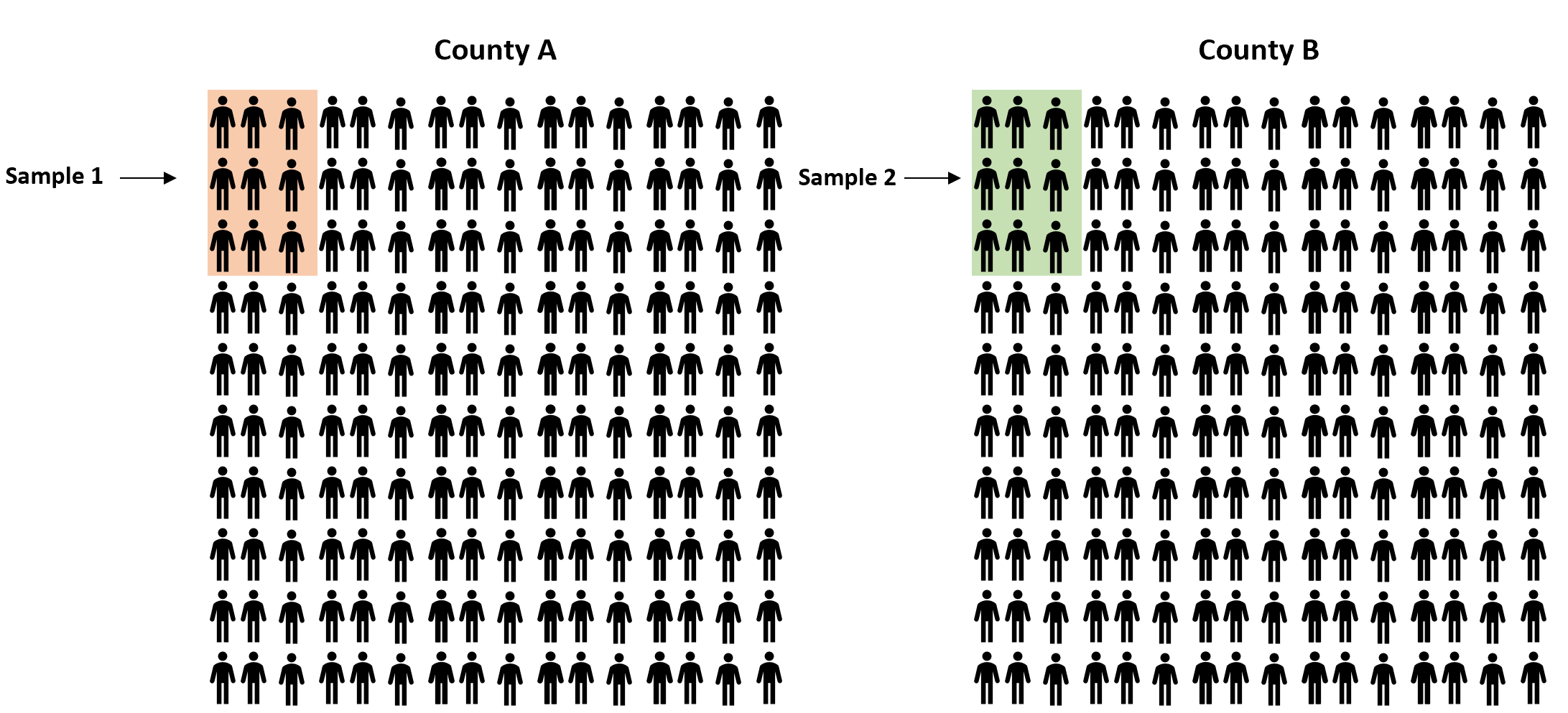
Bununla birlikte, yasayı destekleyen sakinlerin oranının iki örnek arasında en azından biraz farklı olacağı hemen hemen garantidir. Soru, bu farkın istatistiksel olarak anlamlı olup olmadığıdır . Neyse ki iki oranlı z testi bu soruyu yanıtlamamıza olanak tanıyor.

İki oranlı Z testi: formül

İki oranlı bir z testi her zaman aşağıdaki boş hipotezi kullanır:

• H ₀ : μ ₁ = μ ₂ (iki popülasyon oranı eşittir)

Alternatif hipotez iki taraflı, sol veya sağ olabilir:

• H ₁ (iki kuyruklu): π ₁ ≠ π ₂ (iki popülasyon oranı eşit değildir)
• H ₁ (solda): π ₁ < π ₂ (nüfus 1’in oranı, nüfus 2’nin oranından azdır)
• H ₁ (sağ): π ₁ > π ₂ (nüfus 1’in oranı, nüfus 2’nin oranından daha büyüktür)

Z testi istatistiğini hesaplamak için aşağıdaki formülü kullanırız:

z = (p ₁ -p ₂ ) / √ p(1-p)(1/n ₁ +1/n ₂ )

burada p ₁ ve p ₂ örnek oranlarıdır, n ₁ ve n ₂ örnek boyutlarıdır ve p aşağıdaki şekilde hesaplanan toplam havuzlanmış orandır:

p = (p ₁ n ₁ + p ₂ n ₂ )/(n ₁ + n ₂ )

Z testi istatistiğine karşılık gelen p değeri seçilen anlamlılık seviyesinden küçükse (ortak seçenekler 0,10, 0,05 ve 0,01’dir), o zaman sıfır hipotezini reddedebilirsiniz.

İki oranlı Z testi : örnek

A İlçesinde belirli bir yasayı destekleyen sakinlerin oranı ile B İlçesinde yasayı destekleyen sakinlerin oranı arasında bir fark olup olmadığını bilmek istediğimizi varsayalım.

Bunu test etmek için aşağıdaki adımları kullanarak α = 0,05 anlamlılık düzeyinde iki oranlı bir z testi gerçekleştireceğiz:

Adım 1: Örnek verileri toplayın.

Her ilçeden rastgele bir sakin örneği topladığımızı ve aşağıdaki bilgileri elde ettiğimizi varsayalım:

Örnek 1:

• Örneklem büyüklüğü n ₁ = 50
• Kanun lehine oran p ₁ = 0,67

Örnek 2:

• Örneklem büyüklüğü n ₂ = 50
• Kanun lehine oran p ₂ = 0,57

Adım 2: Varsayımları tanımlayın.

İki oranlı z testini aşağıdaki hipotezlerle gerçekleştireceğiz:

• H ₀ : π ₁ = π ₂ (iki popülasyon oranı eşittir)
• H ₁ : π ₁ ≠ π ₂ (iki popülasyon oranı eşit değildir)

Adım 3: z testi istatistiğini hesaplayın.

Öncelikle toplam havuz oranını hesaplayacağız:

p = (p ₁ n ₁ + p ₂ n ₂ )/(n ₁ +n ₂ ) = (0,67(50) + 0,57(50))/(50+50) = 0,62

Daha sonra z testi istatistiğini hesaplayacağız:

z = (p ₁ -p ₂ ) / √ p(1-p)(1/n ₁ +1/n ₂ ) = (.67-.57) / √ .62(1-.62)(1/50 + 1/50 ) = 1,03

Adım 4: z testi istatistiğinin p değerini hesaplayın.

P değeri Z puanı hesaplayıcısına göre z = 1,03 ile ilişkili iki kuyruklu p değeri 0,30301’dir .

Adım 5: Bir sonuç çıkarın.

Bu p değeri bizim anlamlılık düzeyimiz olan α = 0,05’ten düşük olmadığı için sıfır hipotezini reddedemiyoruz. Bu yasayı destekleyen sakinlerin oranının iki ilçe arasında farklı olduğunu söyleyecek yeterli kanıtımız yok.

Not: Bu iki oranlı Z testinin tamamını, iki oranlı Z testi hesaplayıcısını kullanarak da gerçekleştirebilirsiniz.

Ek kaynaklar

Aşağıdaki eğitimlerde çeşitli istatistiksel yazılımlar kullanılarak iki oranlı z testinin nasıl gerçekleştirileceği açıklanmaktadır:

Excel’de iki oranlı Z testi nasıl yapılır
SAS’ta iki oranlı Z testi nasıl yapılır
İki Oranlı Z Testi Hesaplayıcı