Z puanının sağındaki alan nasıl bulunur (örneklerle)
İstatistiklerde z-puanı bize belirli bir değerin popülasyon ortalamasından kaç standart sapma olduğunu söyler.
Belirli bir değere ilişkin z-puanını hesaplamak için aşağıdaki formülü kullanırız:
z = (x – μ) / σ
Altın:
- x : Bireysel verilerin değeri
- μ : Nüfus ortalaması
- σ : Nüfus standart sapması
Belirli bir z-puanının sağında yer alan normal dağılım altındaki alanı bulmak için iki yöntemden birini kullanabiliriz:
1. z tablosunu kullanın.
2. Z-puanı hesaplayıcısının sağındaki kutuyu kullanın.
Aşağıdaki örnekler bu yöntemlerin her birinin pratikte nasıl kullanılacağını göstermektedir.
Örnek 1: Negatif Z puanının sağındaki alan
Belirli bir yunus türünün ağırlığı, ortalama μ = 300 pound ve standart sapma σ = 15 pound ile normal olarak dağıtılır. Yunusların yaklaşık yüzde kaçı 284 poundun üzerindedir?
284 poundluk bir ağırlığın z-puanı şu şekilde hesaplanacaktır: z = (284 – 300) / 15 = -1,07
Bu z-puanının sağındaki alanı bulmak için iki yöntemden birini kullanabiliriz:
Yöntem 1: z tablosunu kullanın.
Z-puanının sağındaki alanı bulmak için z-tablosunda -1,07 değerini arayabiliriz:
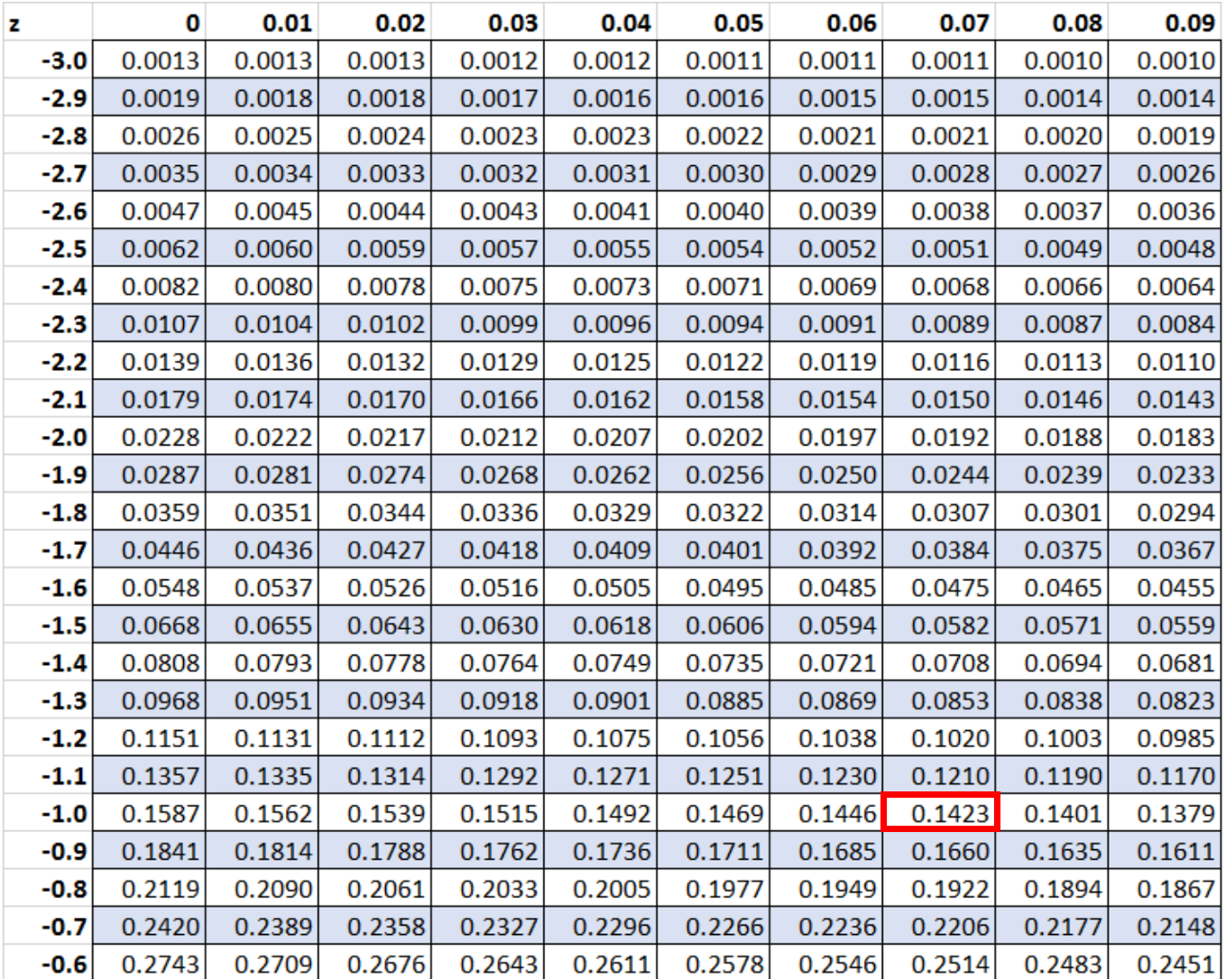
Bu, z = -1,07’nin solundaki alanı temsil eder. Böylece sağdaki alan şu şekilde hesaplanır: 1 – 0,1423 = veya 0,8577 .
Senaryomuza uygulandığında bu, yunusların yaklaşık %85,77’sinin 284 pound’dan daha ağır olduğu anlamına gelir.
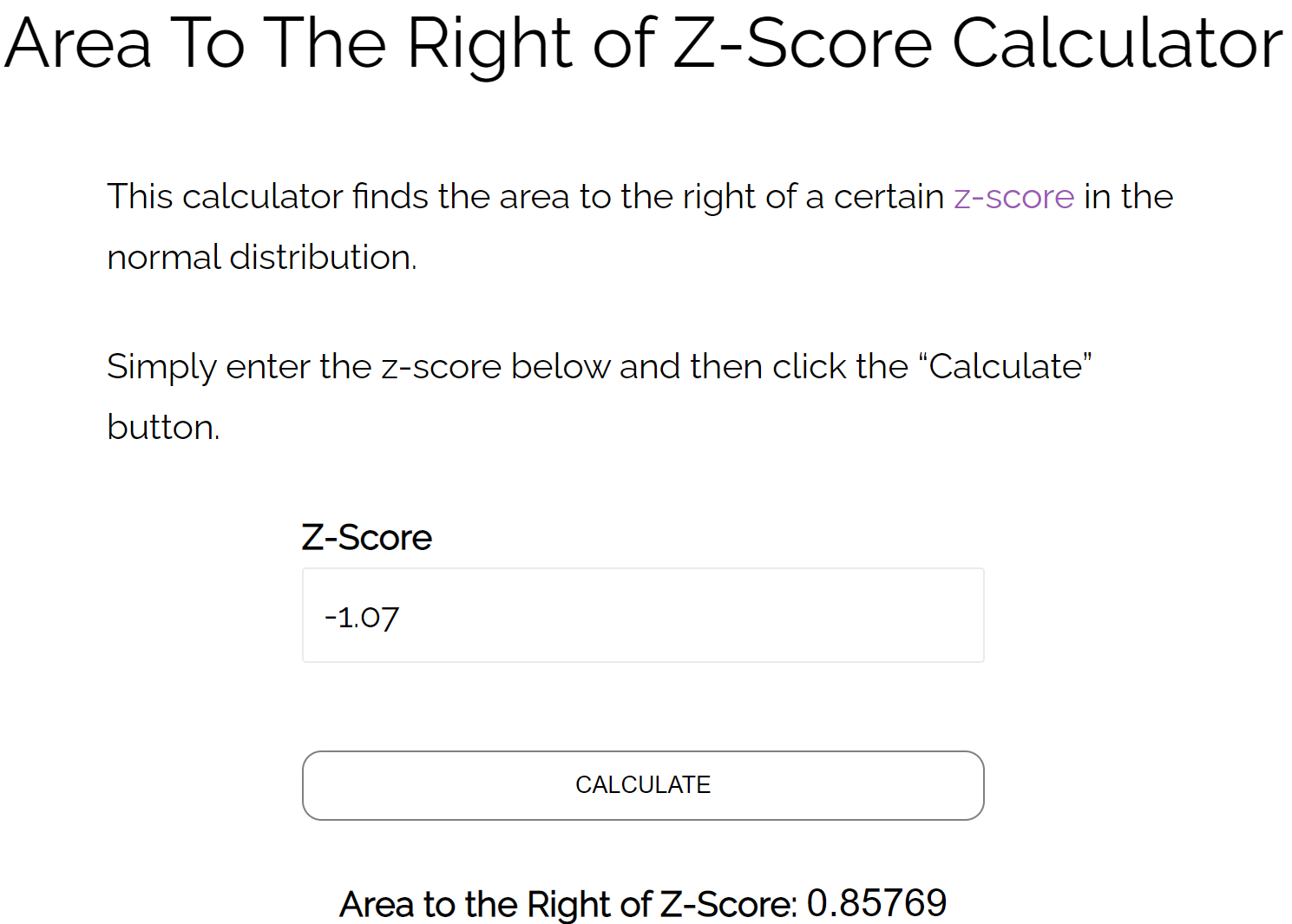
Yöntem 2: Z puanı hesaplayıcının sağındaki kutuyu kullanın
Z = -1,07’nin sağındaki alanın 0,8577 olduğunu bulmak için Z puanı hesaplayıcısının sağındaki alanı da kullanabiliriz.
Örnek 2: Pozitif Z puanının sağındaki alan
Belirli bir sınavdaki puanlar ortalama μ = 85 ve standart sapma σ = 8 ile normal olarak dağıtılır. Öğrencilerin yaklaşık yüzde kaçı sınavda 87’nin üzerinde puan alıyor?
87 puanlık sınav puanının z puanı şu şekilde hesaplanacaktır: z = (87 – 85) / 8 = 0,25.
Bu z-puanının sağındaki alanı bulmak için iki yöntemden birini kullanabiliriz:
Yöntem 1: z tablosunu kullanın.
Z-puanının sağındaki alanı bulmak için z-tablosunda 0,25 değerini aramamız yeterlidir:

z = 0,25’in solundaki alanı temsil eder. Böylece sağdaki alan şu şekilde hesaplanır: 1 – 0,5987 = 0,4013 . Senaryomuza uygulandığında bu, öğrencilerin yaklaşık %40,13’ünün bu sınavda 87’nin üzerinde puan aldığı anlamına gelir.
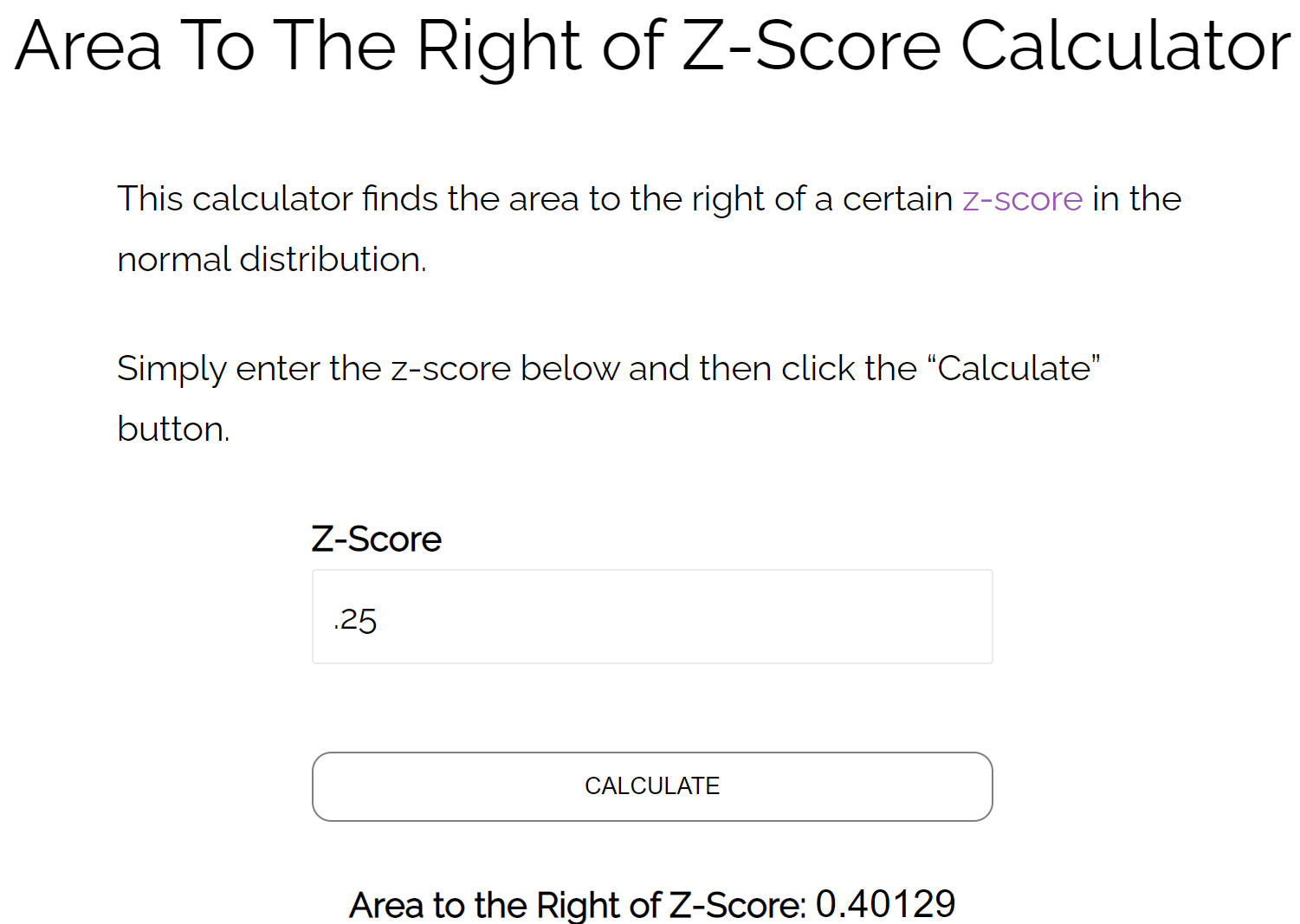
Yöntem 2: Z puanı hesaplayıcının sağındaki kutuyu kullanın
Z = 0,25’in sağındaki alanın 0,4013 olduğunu bulmak için Z puanı hesaplayıcısının sağındaki alanı da kullanabiliriz.
Ek kaynaklar
Aşağıdaki eğitimler z puanlarının kullanımına ilişkin ek bilgiler sağlar:
Z-Skorunun solundaki alan nasıl bulunur?
Belirli bir alanda Z puanları nasıl bulunur?
İyi bir Z-Skoru olarak kabul edilen şey nedir?
Z puanından P değeri manuel olarak nasıl hesaplanır?