Введення в біноміальний розподіл

Біноміальний розподіл є одним із найпопулярніших розподілів у статистиці. Щоб зрозуміти біноміальний розподіл, спочатку варто зрозуміти біноміальні експерименти .

Біноміальні досліди

Біноміальний експеримент — це експеримент, який має такі властивості:

• Експеримент складається з n повторних спроб.
• Кожне випробування має лише два можливі результати.
• Імовірність успіху, позначена p , однакова для кожного випробування.
• Кожен тест незалежний.

Найбільш очевидним прикладом біноміального експерименту є підкидання монети. Наприклад, скажімо, ми підкинули монету 10 разів. Це біноміальний експеримент, оскільки він має такі чотири властивості:

• Експеримент складається з n повторних спроб – Є 10 спроб.
• Кожне випробування має лише два можливі результати: орла або решка.
• Імовірність успіху, позначена p , однакова для кожного випробування. Якщо ми визначаємо «успіх» як посадочні голови, то ймовірність успіху становить рівно 0,5 для кожного випробування.
• Кожне випробування є незалежним – результат одного підкидання монети не впливає на результат будь-якого іншого підкидання монети.

Біноміальний розподіл

Біноміальний розподіл описує ймовірність отримання k успіхів у n біноміальних експериментах.

Якщо випадкова величина X відповідає біноміальному розподілу, то ймовірність успіху X = k можна знайти за такою формулою:

P(X=k) = _n C _k * p ^k * (1-p) ^nk

золото:

• n: кількість випробувань
• k: кількість успіхів
• p: ймовірність успіху в даному випробуванні
• _n C _k : кількість способів отримати k успіхів у n випробуваннях

Наприклад, припустимо, що ми кидаємо монету 3 рази. Ми можемо використати наведену вище формулу, щоб визначити ймовірність отримати 0, 1, 2 і 3 голови в цих 3 підкиданнях:

P(X=0) = ₃ C ₀ * 0,5 ⁰ * (1-0,5) ^3-0 = 1 * 1 * (0,5) ³ = 0,125

P(X=1) = ₃ C ₁ * 0,5 ¹ * (1-0,5) ^3-1 = 3 * 0,5 * (0,5) ² = 0,375

P(X=2) = ₃ C ₂ * 0,5 ² * (1-0,5) ^3-2 = 3 * 0,25 * (0,5) ¹ = 0,375

P(X=3) = ₃ C ₃ * 0,5 ³ * (1-0,5) ^3-3 = 1 * 0,125 * (0,5) ⁰ = 0,125

Примітка : ми використовували цей комбінований калькулятор для обчислення _{nCk для} кожного прикладу.

Ми можемо створити просту гістограму, щоб візуалізувати цей розподіл ймовірностей:

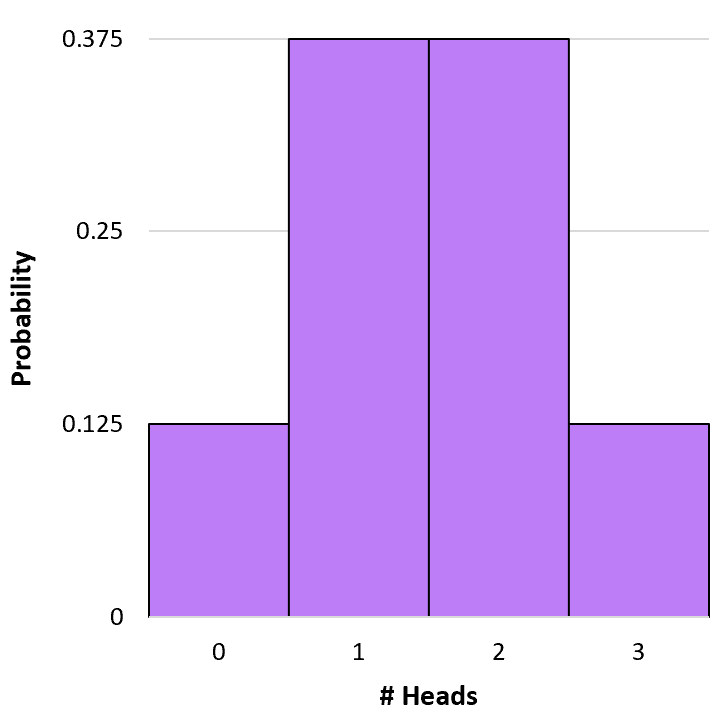
Обчислення кумулятивних біноміальних ймовірностей

За допомогою наведеної вище формули легко обчислити окрему біноміальну ймовірність (наприклад, ймовірність того, що монета випаде головами 1 раз із 3 кидків), але для обчислення сукупної біноміальної ймовірності нам потрібно додати окремі ймовірності.

Наприклад, скажімо, ми хочемо знати ймовірність того, що монета випаде вгору 1 раз або менше з 3 кидків. Щоб обчислити цю ймовірність, ми використаємо таку формулу:

P(X≤1) = P(X=0) + P(X=1) = 0,125 + 0,375 = 0,5 .

Це називається кумулятивною ймовірністю , оскільки вона передбачає додавання кількох ймовірностей. Ми можемо обчислити кумулятивну ймовірність отримання k голів або менше для кожного результату за подібною формулою:

P(X≤0) = P(X=0) = 0,125 .

P(X≤1) = P(X=0) + P(X=1) = 0,125 + 0,375 = 0,5 .

P(X≤2) = P(X=0) + P(X=1) + P(X=2) = 0,125 + 0,375 + 0,375 = 0,875 .

P(X≤3) = P(X=0) + P(X=1) + P(X=2) + P(X=3) = 0,125 + 0,375 + 0,375 + 0,125 = 1 .

Ми можемо створити гістограму, щоб візуалізувати цей кумулятивний розподіл ймовірностей:

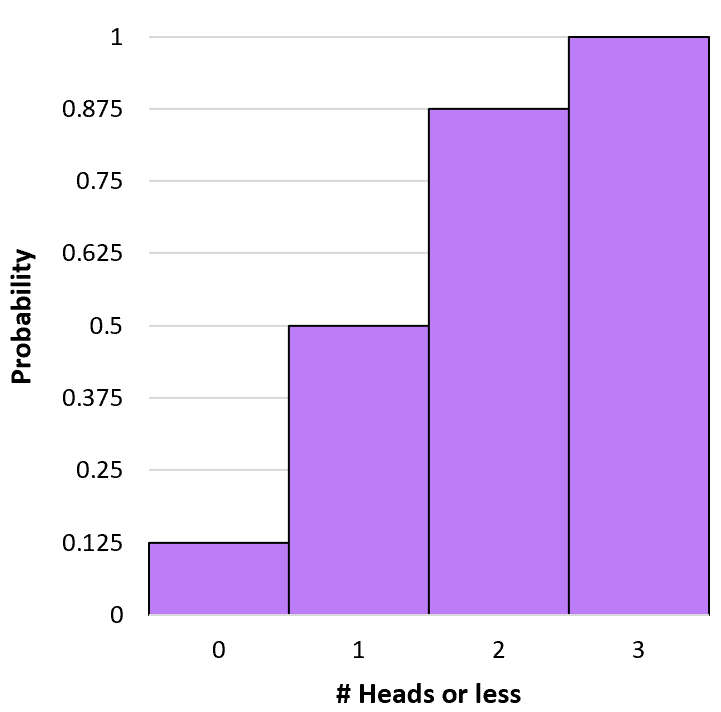
Калькулятор біноміальної ймовірності

Коли ми працюємо з невеликими числами (наприклад, 3 підкидання монети), доцільно обчислювати біноміальні ймовірності вручну. Однак, коли ми працюємо з більшими числами (наприклад, 100 тиражів), може бути важко обчислити ймовірності вручну. У цих випадках може бути корисним використання калькулятора біноміальної ймовірності, подібного до наведеного нижче.

Наприклад, припустимо, що ми кидаємо монету n = 100 разів, імовірність того, що вона впаде на голови в даному випробуванні, становить p = 0,5, і ми хочемо знати ймовірність того, що вона впаде на голови k = 43 рази або менше:

Ось як інтерпретувати результат:

• Імовірність того, що монета випаде головами рівно 43 рази, становить 0,03007 .
• Імовірність того, що монета випаде менше 43 разів, становить 0,06661 .
• Імовірність того, що монета випаде 43 рази або менше, становить 0,09667 .
• Імовірність того, що монета випаде вгору більш ніж 43 рази, становить 0,90333 .
• Імовірність того, що монета випаде вгору 43 або більше разів, становить 0,93339 .

Властивості біноміального розподілу

Біноміальний розподіл має такі властивості:

Середнє значення розподілу μ = np

Дисперсія розподілу σ ² = np(1-p)

Стандартне відхилення розподілу σ = √ np(1-p)

Наприклад, припустимо, що ми кидаємо монету 3 рази. Нехай p = ймовірність того, що монета впаде на голови.

Середня кількість голів, яку ми очікуємо, становить μ = np = 3*,5 = 1,5 .

Дисперсія кількості голів, яку ми очікуємо, становить σ ² = np(1-p) = 3*,5*(1-,5) = 0,75 .

Практичні задачі біноміального розподілу

Використовуйте наведені нижче практичні завдання, щоб перевірити свої знання про біноміальний розподіл.

Проблема 1

Запитання: Боб виконує 60% своїх штрафних кидків. Якщо він виконує 12 штрафних кидків, яка ймовірність того, що він зробить рівно 10?

Відповідь: використовуючи наведений вище калькулятор біноміального розподілу з p = 0,6, n = 12 і k = 10, ми знаходимо, що P(X=10) = 0,06385 .

Проблема 2

Запитання: Джессіка кидає монету 5 разів. Яка ймовірність того, що монета випаде головою 2 рази чи менше?

Відповідь: Використовуючи наведений вище калькулятор біноміального розподілу з p = 0,5, n = 5 і k = 2, ми знаходимо, що P(X≤2) = 0,5 .

Проблема 3

Запитання: Імовірність того, що даного студента зарахують до певного коледжу, становить 0,2. Якщо подано 10 студентів, яка ймовірність того, що буде прийнято більше ніж 4?

Відповідь: Використовуючи наведений вище калькулятор біноміального розподілу з p = 0,2, n = 10 і k = 4, ми знаходимо, що P(X>4) = 0,03279 .

Проблема 4

Запитання: Ви кидаєте монету 12 разів. Яка очікувана середня кількість голів, що з’являться?

Відповідь: Згадайте, що середнє біноміального розподілу обчислюється як μ = np. Отже, μ = 12*0,5 = 6 голів .

Проблема 5

Запитання: Марк робить хоумран у 10% своїх спроб. Якщо він виконує 5 спроб у певній грі, якою буде різниця в кількості хоумранів, які він виконує?

Відповідь: Згадайте, що дисперсія біноміального розподілу обчислюється як σ ² = np(1-p). Таким чином, ^σ2 = 6*.1*(1-.1) = 0.54 .

Додаткові ресурси

Наступні статті можуть допомогти вам дізнатися, як використовувати біноміальний розподіл у різних статистичних програмах:

• Як обчислити біноміальні ймовірності в Excel
• Як обчислити біноміальні ймовірності на калькуляторі TI-84
• Як обчислити біноміальні ймовірності в R
• Як побудувати графік біноміального розподілу в R