Що таке вибірковий простір? визначення та приклади

Вибірковий простір експерименту – це набір усіх можливих результатів експерименту.

Наприклад, припустімо, що ми один раз кидаємо кубик. Простір вибірки можливих результатів включає:

Простір вибірки = 1, 2, 3, 4, 5, 6

Використовуючи позначення, ми запишемо зразок символу пробілу як курсив S і результати в дужках таким чином:

S = {1, 2, 3, 4, 5, 6}

Приклади вибіркових просторів

Ось кілька додаткових прикладів пробних просторів:

Приклад 1: нічия

Припустимо, ми один раз кидаємо монету. Якщо ми припустимо, що H = монета падає на орла, а T = монета падає на решку, то вибірковий простір для цього підкидання монети буде таким:

S = {H, T}

Приклад 2: кульки в мішку

Припустімо, що ми навмання вибираємо кульку з мішка, що містить три кульки: червону кульку, зелену кульку та синю кульку. Якщо R = червоний, G = зелений і B = синій, то простір вибірки:

S = {R, G, B}

Приклад 3: підкидання монети та кубика

Припустімо, ми кидаємо монету і кидаємо кубик одночасно. Якщо ми дозволимо H1 представляти результат “Head” і “1”, то вибірковий простір для результатів буде:

S = {H1, H2, H3, H4, H5, H6, T1, T2, T3, T4, T5, T6}

Основний принцип рахунку

Основним принципом підрахунку є спосіб обчислення загальної кількості потенційних результатів експерименту.

Цей принцип стверджує, що якщо подія A має n різних результатів, а подія B має m різних результатів, то загальну кількість потенційних результатів можна обчислити таким чином:

Загальні результати = m * n

Приклад 1: підкидання монети та кубика

Наприклад, якщо ми підкидаємо монету і кидаємо кубик одночасно, то загальну кількість результатів у вибірковому просторі можна обчислити таким чином:

Загальні результати = (2 способи падіння монети) * (6 способів падіння кубика) = 12 можливих результатів.

Ми записали ці 12 результатів у попередньому прикладі:

S = {H1, H2, H3, H4, H5, H6, T1, T2, T3, T4, T5, T6}

Приклад 2: Підрахунок комбінацій одягу

Цей принцип також можна використовувати для обчислення загальних результатів у вибірці для більш ніж двох подій.

Наприклад, припустимо, що випадкова шухляда містить 3 різні сорочки, 4 різні штани та 2 різні шкарпетки. Якщо ми випадково виберемо по одному предмету одягу, не дивлячись, загальна кількість можливих нарядів буде розрахована таким чином:

Загальна кількість нарядів = 3 * 4 * 2 = 24 можливих нарядів

Візуалізація пробних просторів за допомогою деревоподібних діаграм

Коли кількість результатів у вибірковому просторі велика, може бути корисним побудувати деревоподібну діаграму для візуалізації різних комбінацій результатів.

Наприклад, припустимо, що в шафі є 2 різні сорочки, 2 різні штани та 2 різні шкарпетки. Якщо ми випадково виберемо по одному предмету одягу, не дивлячись, загальну кількість можливих нарядів можна візуалізувати таким чином:

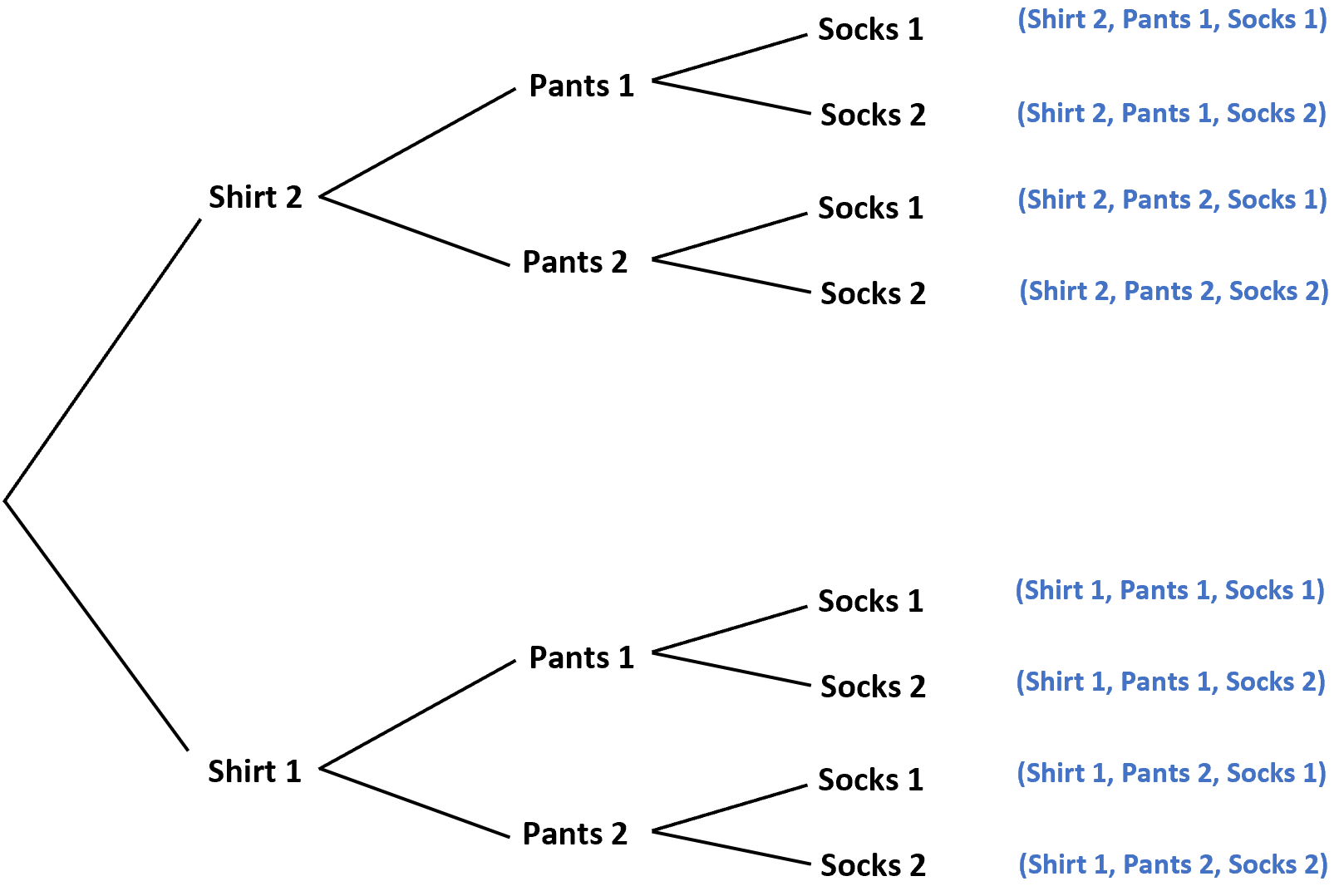
Ця діаграма допомагає нам візуалізувати вісім різних потенційних результатів у просторі вибірки.

Ми також можемо використати фундаментальний принцип підрахунку, щоб підтвердити, що має бути вісім різних результатів:

Загальний результат = 2 сорочки * 2 штани * 2 шкарпетки = 8 можливих нарядів

Обчислення ймовірностей результатів у вибіркових просторах

Після того, як ми визначили вибірковий простір експерименту, ми можемо обчислити ймовірність події A , використовуючи таку формулу:

P(A) = (простір вибірки A) / (загальний простір вибірки)

Наприклад, припустімо, що ми один раз кидаємо кубик. Зразок простору можна записати у вигляді:

S = {1, 2, 3, 4, 5, 6}

Якщо ми визначимо подію А як падіння кубика на число «2», то вибірковий простір події А можна записати так:

S = {2}

Таким чином, ймовірність події А можна розрахувати так:

P(A) = 1/6

Якщо ми визначимо подію А як приземлення кубика на парне число, то вибірковий простір події А можна записати так:

S = {2, 4, 6}

Таким чином, ймовірність події А можна розрахувати так:

P(A) = 3/6