Вибірковий розподіл різниці середніх

за Редакція 3 Серпня, 2023 Статистика 0 коментарів

У цій статті пояснюється, що таке вибірковий розподіл різниці між двома середніми в статистиці. Ви також знайдете формулу для вибіркового розподілу різниці середніх і, крім того, покрокову вправу.

Що таке вибірковий розподіл різниці середніх?

Вибірковий розподіл різниці в середніх – це розподіл, який є результатом обчислення відмінностей між середніми значеннями всіх можливих вибірок із двох різних сукупностей.

Тобто, щоб отримати вибірковий розподіл різниці середніх, необхідно відібрати всі можливі вибірки з двох досліджуваних популяцій, потім розрахувати середнє значення кожної вибраної вибірки і, нарешті, різницю між усіма середніми, розрахованими з двох популяцій. Таким чином, набір значень, отриманих після застосування всіх цих операцій, формує вибірковий розподіл різниці середніх.

Різниця вибіркового розподілу середніх використовується для обчислення ймовірності того, що різниця між двома середніми випадково відібраними вибірками з двох різних сукупностей близька до різниці середніх сукупностей.

➤ Див.: Вибірковий розподіл середнього значення

Формула для вибіркового розподілу різниці середніх

Якщо розмір вибірки достатньо великий (n ₁ ≥30 і n ₂ ≥30), вибірковий розподіл різниці середніх має нормальний розподіл. Точніше, параметри зазначеного розподілу розраховуються наступним чином:

$\begin{array}{c}\displaystyle \mu_{\overline{x_1}-\overline{x_2}}=\mu_1-\mu_2 \qquad \sigma_{\overline{x_1}-\overline{x_2}}=\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}\\[6ex]\displaystyle N_{\overline{x_1}-\overline{x_2}}\left(\mu_1-\mu_2, \sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}\right) \end{array}$

Примітка. Якщо обидві генеральні сукупності є нормальними розподілами , тоді вибірковий розподіл різниці середніх відповідає нормальному розподілу незалежно від розмірів вибірки.

Отже, оскільки вибірковий розподіл різниці середніх визначається нормальним розподілом, формула для розрахунку статистики вибіркового розподілу різниці середніх має вигляд:

$Z=\cfrac{(\overline{x_1}-\overline{x_2})-(\mu_1-\mu_2)}{\displaystyle\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}}$

золото:

$\overline{x_i}$

є середнім значенням вибірки i.
$\mu_i$

це середнє значення населення i.
$\sigma_i$

є стандартним відхиленням сукупності i.
$n_i$

це розмір вибірки i.
$Z$

є змінною, визначеною стандартним нормальним розподілом N(0,1).

Зауважте, що вибірки з різних сукупностей можуть мати різні розміри вибірки.

Конкретний приклад вибіркового розподілу різниці середніх

Коли ми побачимо визначення різниці вибіркового розподілу середніх і його формулу, ми побачимо покроковий приклад, щоб завершити розуміння концепції різниці вибіркового розподілу середніх.

У статистичному дослідженні ми хочемо проаналізувати різницю між ростом хлопчиків і дівчаток певного віку. Ми знаємо, що розподіл, який визначає популяцію хлопчиків цього віку, має середнє значення 157 см і стандартне відхилення 9 см, а з іншого боку, розподіл, який визначає популяцію дівчаток цього віку, має середнє значення 148 см. см і стандартним відхиленням 7 см. Якщо відібрати вибірку з 30 хлопчиків цього віку та вибірку з 35 дівчаток цього віку, яка ймовірність того, що середній зріст вибірки хлопчиків буде на 12 см більший за середній зріст вибірки дівчаток?

Для вирішення цієї проблеми перше, що потрібно зробити, це розрахувати статистику різниці вибіркового розподілу середніх. Тому ми застосовуємо формулу, наведену вище:

$Z=\cfrac{(\overline{x_1}-\overline{x_2})-(\mu_1-\mu_2)}{\displaystyle\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}\right)}=\cfrac{12-(157-148)}{\displaystyle\sqrt{\frac{9^2}{30}+\frac{7^2}{35}}}=1,48$

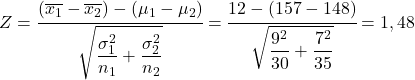
Тому ймовірність того, що середній зріст хлопчиків на 12 см перевищує середній зріст дівчаток, еквівалентна ймовірності того, що змінна Z перевищує 1,48.

$P[(\overline{x_1}-\overline{x_2})>12]=P[Z>1,48]” title=”Rendered by QuickLaTeX.com” height=”19″ width=”253″ style=”vertical-align: -5px;”></p> </p> <p> Тому ми шукаємо ймовірність Z>1,48 у <a href=$ таблиці Z :

$P[(\overline{x_1}-\overline{x_2})>12]=P[Z>1,48]=0,0694″ title=”Rendered by QuickLaTeX.com” height=”19″ width=”331″ style=”vertical-align: -5px;”></p> </p> <p> Коротше кажучи, ймовірність того, що середній зріст хлопчиків на 12 см перевищує середній зріст дівчаток, становить 6,94%.</p> </div>  <div class=$

Про автора

Редакція

Привіт, я Бенджамін, професор статистики на пенсії, який став викладачем статистики. Маючи великий досвід і знання в галузі статистики, я готовий поділитися своїми знаннями, щоб розширити можливості студентів через Statorials. Дізнайтеся більше

Що таке вибірковий розподіл різниці середніх?

Формула для вибіркового розподілу різниці середніх

Конкретний приклад вибіркового розподілу різниці середніх

Про автора

Редакція

Додати коментар