Негативний біноміальний розподіл
У цій статті пояснюється, що таке від’ємний біноміальний розподіл і для чого він використовується. Ви також знайдете формулу для від’ємного біноміального розподілу, конкретний приклад і властивості цього типу розподілу ймовірностей. Нарешті, ви зможете розрахувати будь-яку ймовірність від’ємного біноміального розподілу за допомогою онлайн-калькулятора.
Що таке від’ємний біноміальний розподіл?
Негативний біноміальний розподіл — це розподіл ймовірностей, який описує кількість спроб Бернуллі, необхідних для отримання певної кількості позитивних результатів.
Отже, негативний біноміальний розподіл має два характерних параметри: r — кількість бажаних успішних результатів і p — ймовірність успіху для кожного проведеного експерименту Бернуллі.
![]()
Пам’ятайте, що тест Бернуллі — це експеримент, який має два можливі результати: «успіх» і «невдача». Отже, якщо ймовірність «успіху» дорівнює p , то ймовірність «невдачі» дорівнює q=1-p .
Таким чином, негативний біноміальний розподіл визначає процес, у якому виконується стільки випробувань Бернуллі, скільки необхідно для отримання позитивних результатів . Крім того, усі ці випробування Бернуллі незалежні та мають постійну ймовірність успіху .
Наприклад, випадкова змінна, яка слідує за негативним біноміальним розподілом, — це кількість кидків кубика, доки число 6 не буде кинуто тричі.
Різниця між негативним біноміальним розподілом і біноміальним розподілом полягає в тому, що негативний біноміальний розподіл підраховує кількість разів, необхідних для отримання певної кількості успішних результатів, тоді як біноміальний розподіл підраховує кількість успішних випадків у серії тестів Бернуллі.
Формула від’ємного біноміального розподілу
Враховуючи параметри r, p, x, ймовірність від’ємного біноміального розподілу обчислюється множенням комбінаторного числа x-1 у xr на (1-p) xr на p r .
Отже, формула для обчислення ймовірності від’ємного біноміального розподілу :

👉 Ви можете скористатися наведеним нижче калькулятором, щоб обчислити ймовірність змінної, яка відповідає від’ємному біноміальному розподілу.
Розв’язана вправа від’ємного біноміального розподілу
- Яка ймовірність того, що якщо ви підкинете монету вісім разів, вона випаде орелами вчетверте під час восьмого підкидання?
По-перше, нам потрібно розрахувати ймовірність отримання голів при підкиданні монети. У цьому випадку ми маємо лише один позитивний результат (орла) з двох можливих результатів (орла та решка), тому ймовірність успіху дорівнює:
![]()
Таким чином, випадкова величина в цій задачі має негативний біноміальний розподіл, де r=4 і p=0,5. Тому ми використовуємо формулу від’ємного біноміального розподілу, щоб обчислити ймовірність виконання вправи.
![Rendered by QuickLaTeX.com \begin{aligned}P[X=x]&=\begin{pmatrix}x-1\\ x-r\end{pmatrix}\cdot (1-p)^{x-r}\cdot p^r\\[2ex]\displaystyle P[X=8]&=\begin{pmatrix}8-1\\ 8-4\end{pmatrix}\cdot (1-0,5)^{8-4}\cdot 0,5^4\\[2ex] P[X=8]&=0,1367\end{aligned}](https://statorials.org/wp-content/ql-cache/quicklatex.com-bc56100604e5889a6d169c0395f19ebe_l3.png)
Характеристика від’ємного біноміального розподілу
Нижче наведено найважливіші характеристики від’ємного біноміального розподілу.
- Від’ємний біноміальний розподіл визначається двома характерними параметрами: r — кількість бажаних успішних результатів і p — ймовірність успіху для кожного проведеного експерименту Бернуллі.
*** QuickLaTeX cannot compile formula:
\begin{array}{c}r\in \mathbb{Z}^+ \\[2ex] 0 <ul><li> The mean of the negative binomial distribution is equal to <em>r</em> multiplied by <em>(1-p)</em> and divided by <em>p</em> . Thus the formula which makes it possible to calculate the mean of a negative binomial distribution is the following: </li></ul>[latex]E[X]=\cfrac{r\cdot (1-p)}{p}
*** Error message:
Missing $ inserted.
leading text: \begin{array}{c}
Please use \mathaccent for accents in math mode.
leading text: ...The mean of the binomial distribution born
Please use \mathaccent for accents in math mode.
leading text: ... the negative binomial distribution is
Please use \mathaccent for accents in math mode.
leading text: ...negative binomial distribution is equal to
Please use \mathaccent for accents in math mode.
leading text: ...gative is equal to <em>r</em> multiplied
Please use \mathaccent for accents in math mode.
leading text: ...m> multiplied by <em>(1-p)</em> and divided
Please use \mathaccent for accents in math mode.
leading text: ...the mean of a binomial distribution born
\begin{array} on input line 8 ended by \end{document}.
- Дисперсія від’ємного біноміального розподілу дорівнює r , помноженому на (1-p), поділеному на p 2 .
![]()
- Якщо параметр r більше 1, моду від’ємного біноміального розподілу можна обчислити за такою формулою:
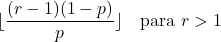
![]()
- Коефіцієнт асиметрії від’ємного біноміального розподілу обчислюється за таким виразом:
![]()
- Ексцес від’ємного біноміального розподілу можна знайти за такою формулою:
![]()
- Якщо параметр r дорівнює 1, то маємо випадок геометричного розподілу .
![]()
Калькулятор негативного біноміального розподілу
Введіть значення параметрів r, p, x в наступний калькулятор, щоб обчислити ймовірність. Ви повинні вводити числа, використовуючи крапку як десятковий роздільник, наприклад 0,50.