Як перевірити припущення anova
Односторонній дисперсійний аналіз є статистичним тестом, який використовується для визначення того, чи існує значна різниця між середніми значеннями трьох або більше незалежних груп.
Ось приклад того, коли ми можемо використовувати односторонній дисперсійний аналіз:
Ви випадковим чином розподіляєте клас із 90 студентів на три групи по 30. Кожна група використовує різну техніку навчання протягом місяця для підготовки до іспиту. Наприкінці місяця всі учні складають однаковий іспит.
Ви хочете знати, чи впливає техніка навчання на результати іспитів. Отже, ви виконуєте односторонній дисперсійний аналіз , щоб визначити, чи існує статистично значуща різниця між середніми балами трьох груп.
Перш ніж ми зможемо виконати односторонній дисперсійний аналіз, ми повинні спочатку переконатися, що виконуються три припущення.
1. Нормальність – кожен зразок був взятий із нормально розподіленої сукупності.
2. Рівні дисперсії – дисперсії популяцій, з яких відбираються зразки, рівні.
3. Незалежність – спостереження в кожній групі є незалежними одне від одного, і спостереження в групах були отримані шляхом випадкової вибірки.
Якщо ці припущення не виконуються, результати нашого одностороннього дисперсійного аналізу можуть бути ненадійними.
У цій статті ми пояснюємо, як перевірити ці припущення та що робити, якщо будь-яке з них порушується.
Припущення №1: нормальність
ANOVA припускає, що кожен зразок був взятий із нормально розподіленої сукупності.
Як перевірити цю гіпотезу в R:
Щоб перевірити цю гіпотезу, ми можемо використати два підходи:
- Візуально перевірте гіпотезу за допомогою гістограм або графіків QQ .
- Перевірте гіпотезу за допомогою формальних статистичних тестів, таких як Шапіро-Вілка, Колмогорова-Смиронова, Жарка-Барре або Д’Агостіно-Пірсона.
Наприклад, припустімо, що ми набираємо 90 людей для участі в експерименті зі схуднення, у якому ми випадковим чином призначаємо 30 осіб для виконання Програми A, Програми B або Програми C протягом одного місяця. Щоб побачити, чи програма впливає на втрату ваги, ми хочемо виконати односторонній дисперсійний аналіз. Наступний код демонструє, як перевірити припущення про нормальність за допомогою гістограм, графіків QQ і тесту Шапіро-Вілка.
1. Підберіть модель ANOVA.
#make this example reproducible
set.seed(0)
#create data frame
data <- data. frame (program = rep(c(" A ", " B ", " C "), each = 30 ),
weight_loss = c(runif(30, 0, 3),
runif(30, 0, 5),
runif(30, 1, 7)))
#fit the one-way ANOVA model
model <- aov(weight_loss ~ program, data = data)
2. Створіть гістограму значень відповіді.
#create histogram
hist(data$weight_loss)
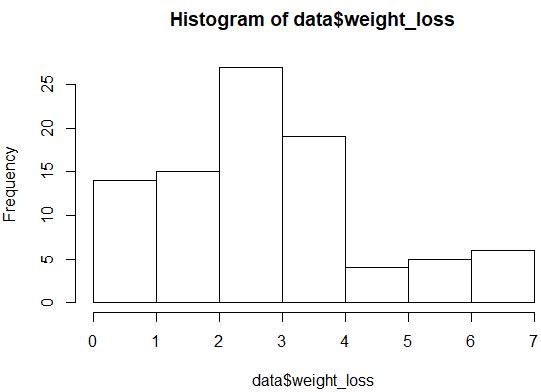
Розподіл виглядає не дуже нормально розподіленим (наприклад, він не має форми дзвоника), але ми також можемо створити графік QQ, щоб по-новому поглянути на розподіл.
3. Створіть QQ графік залишків
#create QQ plot to compare this dataset to a theoretical normal distribution qqnorm(model$residuals) #add straight diagonal line to plot qqline(model$residuals)

Загалом, якщо точки даних лежать уздовж прямої діагональної лінії на графіку QQ, то набір даних, ймовірно, відповідає нормальному розподілу. У цьому випадку ми бачимо помітне відхилення від лінії вздовж кінців, що може вказувати на те, що дані розподілені неправильно.
4. Виконайте тест Шапіро-Вілка на нормалізацію.
#Conduct Shapiro-Wilk Test for normality shapiro. test (data$weight_loss) #Shapiro-Wilk normality test # #data: data$weight_loss #W = 0.9587, p-value = 0.005999
Тест Шапіро-Вілка перевіряє нульову гіпотезу про те, що вибірки походять із нормального розподілу, проти альтернативної гіпотези про те, що вибірки не походять із нормального розподілу. У цьому випадку p-значення тесту становить 0,005999 , що нижче рівня альфа 0,05. Це свідчить про те, що вибірки не дотримуються нормального розподілу.
Що робити, якщо це припущення не виконується:
Загалом, односторонній дисперсійний аналіз вважається досить стійким проти порушень припущення про нормальність, якщо розміри вибірки достатньо великі.
Крім того, якщо у вас є надзвичайно великі вибірки, статистичні тести, такі як тест Шапіро-Вілка, майже завжди скажуть вам, що ваші дані не є нормальними. З цієї причини часто найкраще візуально перевіряти дані за допомогою таких діаграм, як гістограми та графіки QQ. Просто подивившись на графіки, ви можете отримати гарне уявлення про те, чи дані розподіляються нормально чи ні.
Якщо припущення про нормальність серйозно порушено або ви просто хочете бути дуже консервативними, у вас є два варіанти:
(1) Перетворіть значення відповіді ваших даних, щоб розподіли були більш нормальними.
(2) Виконайте еквівалентний непараметричний тест, такий як тест Краскела-Уолліса , який не вимагає припущення нормальності.
Припущення №2: однакова дисперсія
Дисперсійний аналіз припускає, що дисперсії популяцій, з яких відбираються зразки, рівні.
Як перевірити цю гіпотезу в R:
Ми можемо перевірити цю гіпотезу в R за допомогою двох підходів:
- Візуально перевірте гіпотезу за допомогою діаграм.
- Перевірте гіпотезу за допомогою формальних статистичних тестів, таких як тест Бартлетта.
Наступний код демонструє, як це зробити, використовуючи той самий підроблений набір даних про втрату ваги, який ми створили раніше.
1. Створіть коробкові діаграми.
#Create box plots that show distribution of weight loss for each group boxplot(weight_loss ~ program, xlab=' Program ', ylab=' Weight Loss ', data=data)
Розбіжність у втраті ваги в кожній групі можна спостерігати за довжиною кожного бокс-плота. Чим довша коробка, тим вища дисперсія. Наприклад, ми бачимо, що дисперсія трохи вища для учасників програми C порівняно з програмами A та B.
2. Виконайте пробу Бартлетта.
#Create box plots that show distribution of weight loss for each group bartlett. test (weight_loss ~ program, data=data) #Bartlett test of homogeneity of variances # #data: weight_loss by program #Bartlett's K-squared = 8.2713, df = 2, p-value = 0.01599
Тест Бартлетта перевіряє нульову гіпотезу про те, що вибірки мають однакові дисперсії, проти альтернативної гіпотези про те, що вибірки не мають рівних дисперсій. У цьому випадку p-значення тесту становить 0,01599 , що нижче рівня альфа 0,05. Це означає, що не всі зразки мають однакову дисперсію.
Що робити, якщо це припущення не виконується:
Загалом, односторонній дисперсійний аналіз вважається достатньо стійким до порушень припущення рівних дисперсій, якщо кожна група має однаковий розмір вибірки.
Однак, якщо розміри вибірки не однакові, і це припущення серйозно порушено, ви можете натомість запустити тест Крускала-Уолліса , який є непараметричною версією одностороннього дисперсійного аналізу.
Припущення №3: Незалежність
ANOVA передбачає:
- Спостереження кожної групи не залежать від спостережень усіх інших груп.
- Спостереження в кожній групі були отримані шляхом випадкової вибірки.
Як перевірити цю гіпотезу:
Немає жодного формального тесту, який можна використати для перевірки того, що спостереження в кожній групі є незалежними та що вони були отримані шляхом випадкової вибірки. Єдиний спосіб задовольнити це припущення — використовувати рандомізований дизайн.
Що робити, якщо це припущення не виконується:
На жаль, ви мало що можете зробити, якщо це припущення не виконується. Простіше кажучи, якщо дані були зібрані таким чином, що спостереження в кожній групі не були незалежними від спостережень в інших групах, або якщо спостереження в кожній групі не були отримані за допомогою рандомізованого процесу, результати ANOVA не будуть надійними. .
Якщо це припущення не виконується, найкраще відтворити експеримент за допомогою рандомізованого плану.
Подальше читання:
Як виконати односторонній дисперсійний аналіз у R
Як виконати односторонній дисперсійний аналіз в Excel
