Як змоделювати та побудувати графік двовимірного нормального розподілу в r
У статистиці дві змінні відповідають двовимірному нормальному розподілу, якщо вони мають нормальний розподіл при додаванні.
Цей підручник пояснює, як виконувати такі завдання в R:
- Змоделюйте двовимірний нормальний розподіл
- Побудуйте графік двовимірного нормального розподілу за допомогою контурної діаграми (2D графік)
- Побудуйте графік двовимірного нормального розподілу за допомогою графіка поверхні (3D-графіка)
Ходімо!
Приклад 1: моделювання двовимірного нормального розподілу в R
Найпростіший спосіб моделювання двовимірного нормального розподілу в R — це використання функції mvrnorm() з пакету MASS .
Наступний код показує, як використовувати цю функцію для симуляції двовимірного нормального розподілу на практиці:
library (MASS)
#make this example reproducible
set. seed ( 0 )
#simulate bivariate normal distribution
bivariate_data <- as. data . frame (mvrnorm(n= 100 ,
mu=c(0, 0),
Sigma=matrix(c(5, 3, 4, 4), ncol= 2 )))
#view first six rows of bivariate dataset
head(bivariate_data)
V1 V2
1 -2.03600343 -2.9623059
2 0.07719131 1.2948982
3 -3.26729701 -1.7928069
4 -2.62985132 -2.3015471
5 -1.75126215 0.3056698
6 3.67698436 2.2020238
Ось що робить кожен аргумент функції mvrnorm() :
- n : визначає розмір вибірки
- mu : визначає середнє значення кожної змінної
- Сигма : визначає коваріаційну матрицю двох змінних
Кінцевим результатом є фрейм даних із двома змінними, який дотримується нормального розподілу при додаванні разом.
Приклад 2: Побудова двовимірного нормального розподілу
Найпростіший спосіб побудувати графік двовимірного нормального розподілу в R — це використовувати функції в пакеті mnormt() .
Наприклад, ми можемо використати функцію contour() цього пакету для створення контурної діаграми, яка забезпечує 2D візуалізацію двовимірного нормального розподілу:
library (mnormt)
#make this example reproducible
set. seed ( 0 )
#create bivariate normal distribution
x <- seq(-3, 3, 0.1)
y <- seq(-3, 3, 0.1)
mu <- c(0, 0)
sigma <- matrix(c(2, -1, -1, 2), nrow= 2 )
f <- function(x, y) dmnorm(cbind(x, y), mu, sigma)
z <- outer(x, y, f)
#create contour plot
contour(x, y, z)
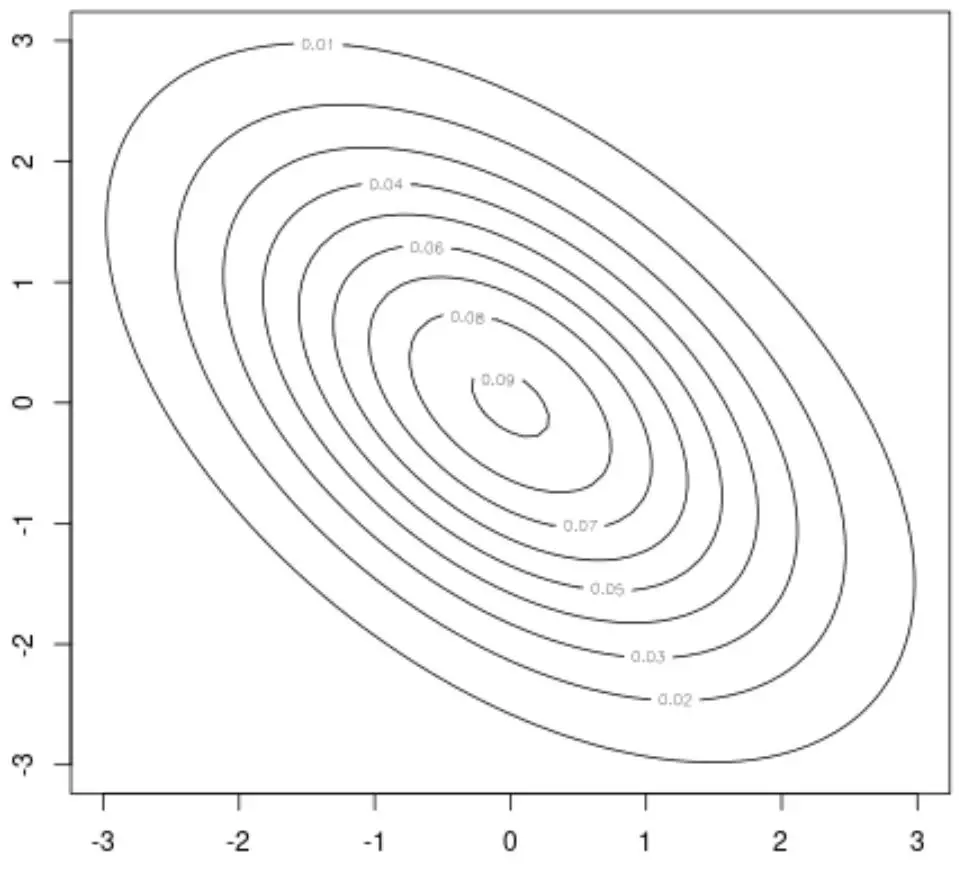
Ми також можемо використовувати функцію persp() для створення графіка поверхні, який забезпечує тривимірну візуалізацію двовимірного нормального розподілу:
library (mnormt)
#make this example reproducible
set. seed ( 0 )
#create bivariate normal distribution
x <- seq(-3, 3, 0.1)
y <- seq(-3, 3, 0.1)
mu <- c(0, 0)
sigma <- matrix(c(2, -1, -1, 2), nrow= 2 )
f <- function(x, y) dmnorm(cbind(x, y), mu, sigma)
z <- outer(x, y, f)
#create surface plot
persp(x, y, z, theta= -30 , phi= 25 , expand= 0.6 , ticktype=' detailed ')
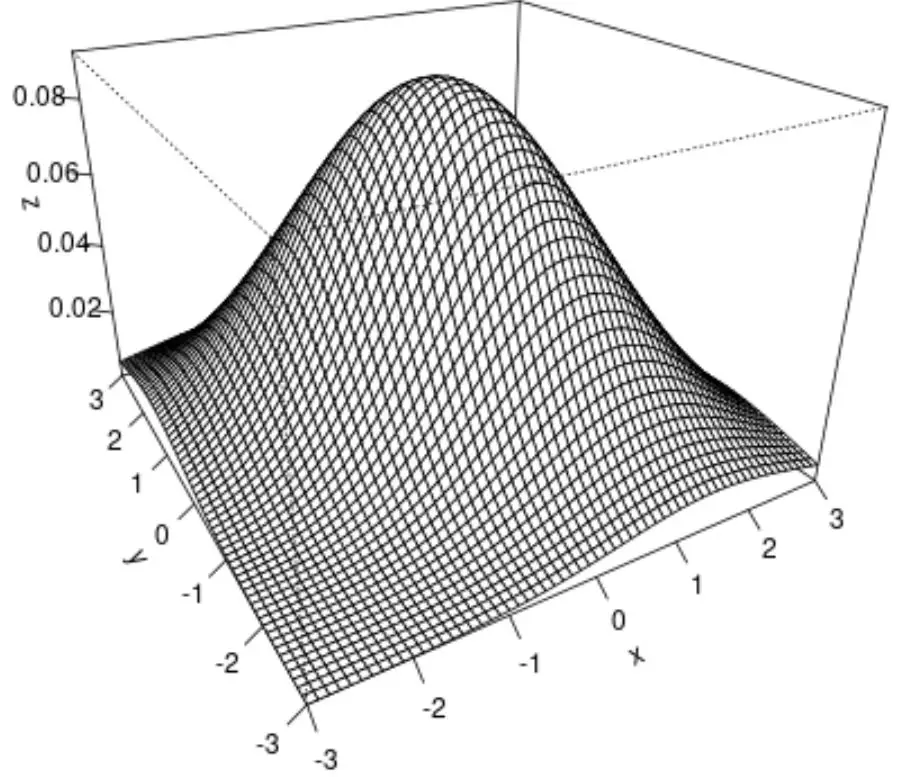
Ось що робить кожен аргумент функції persp() :
- theta, phi : Встановлює кути напрямку перегляду.
- expand : контролює розмір осі z.
- ticktype : контролює появу галочок на осях.
Кінцевим результатом є тривимірний поверхневий графік двовимірного нормального розподілу.
Додаткові ресурси
У наступних посібниках пояснюється, як використовувати інші розподіли ймовірностей у R:
Як використовувати нормальний розподіл у R
Як використовувати біноміальний розподіл у R
Як використовувати розподіл Пуассона в R
Як використовувати мультиноміальний розподіл у R