Як обчислити залишкову суму квадратів у excel

Залишок — це різниця між спостережуваним значенням і прогнозованим значенням у регресійній моделі.

Він розраховується таким чином:

Залишок = спостережуване значення – прогнозоване значення

Один із способів зрозуміти, наскільки регресійна модель відповідає набору даних, — обчислити залишкову суму квадратів , яка обчислюється таким чином:

Залишкова сума квадратів = Σ(e _i ) ²

золото:

• Σ : грецький символ, що означає «сума»
• e _i : i- ^й залишок

Чим менше значення, тим краще модель відповідає набору даних.

У цьому посібнику наведено приклади обчислення залишкової суми квадратів для моделі простої лінійної регресії та моделі множинної лінійної регресії в Excel.

Приклад 1: Залишкова сума квадратів для простої лінійної регресії

Припустімо, що в Excel є такий набір даних:

Щоб обчислити залишкову суму квадратів для простої лінійної регресійної моделі з використанням x як змінної предиктора та y як змінної відповіді, ми можемо використати функцію LINEST() , яка використовує такий синтаксис:

LINEST(відомі_ys; [відомі_xs]; [const]; [статистика])

золото:

• відомі_і: діапазон значень y
• відомий_sx: діапазон значень x
• const: чи змусити константу b дорівнювати нулю. Ми залишимо це поле порожнім.
• stats: список статистики регресії. Ми уточнимо, що це ПРАВДА.

На наступному знімку екрана показано, як використовувати цю функцію на практиці:

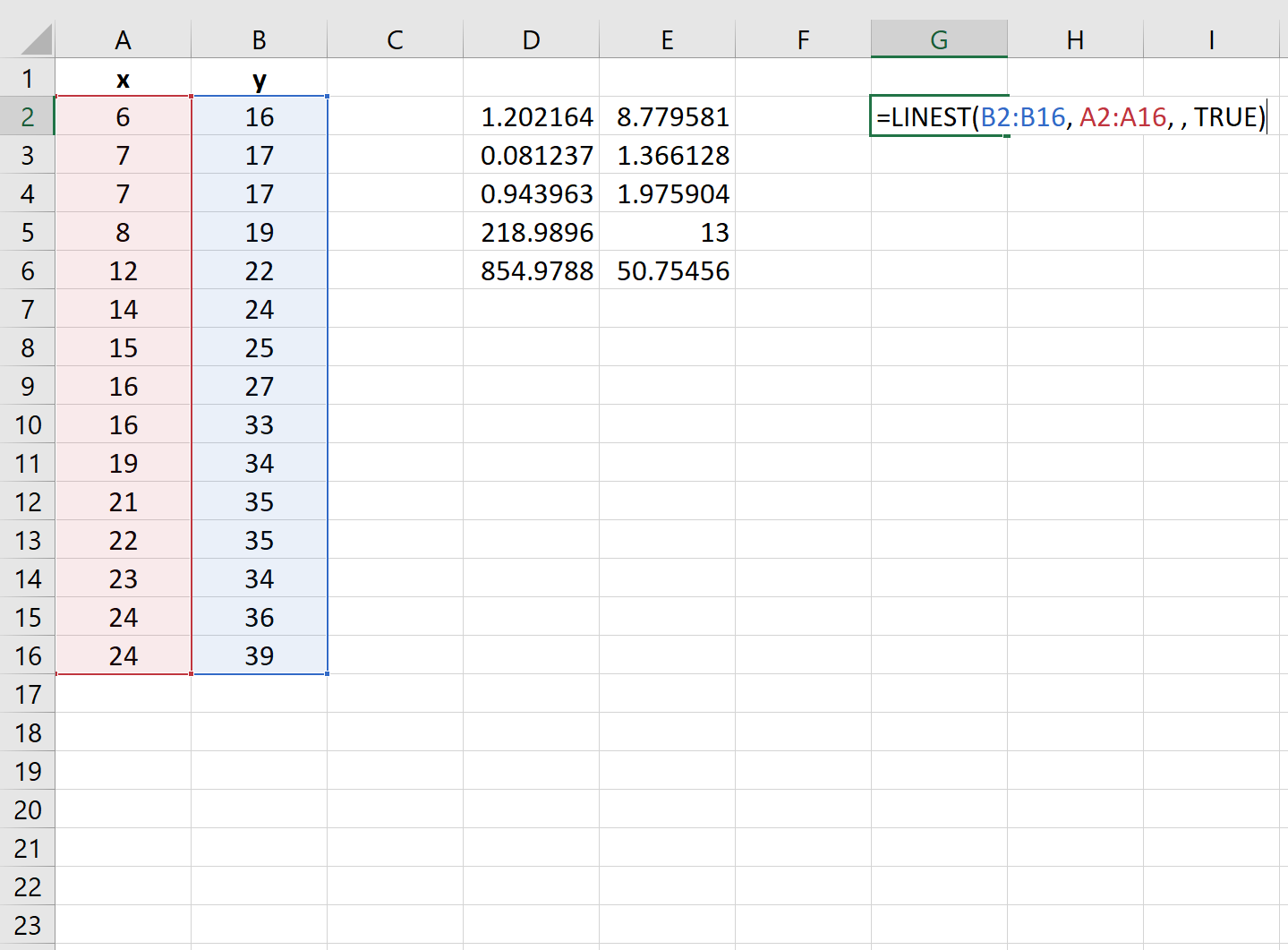
Залишкова сума квадратів регресійної моделі відображається в останній клітинці другого стовпця вихідних даних. У цьому прикладі залишкова сума квадратів дорівнює 50,75 .

Приклад 2: Залишкова сума квадратів для множинної лінійної регресії

Припустімо, що в Excel є такий набір даних:

Знову ж таки, ми можемо використовувати функцію LINEST(), щоб обчислити залишкову суму квадратів моделі.

Єдина відмінність полягає в тому, що ми вкажемо два стовпці значень для аргументу unknown_xs :

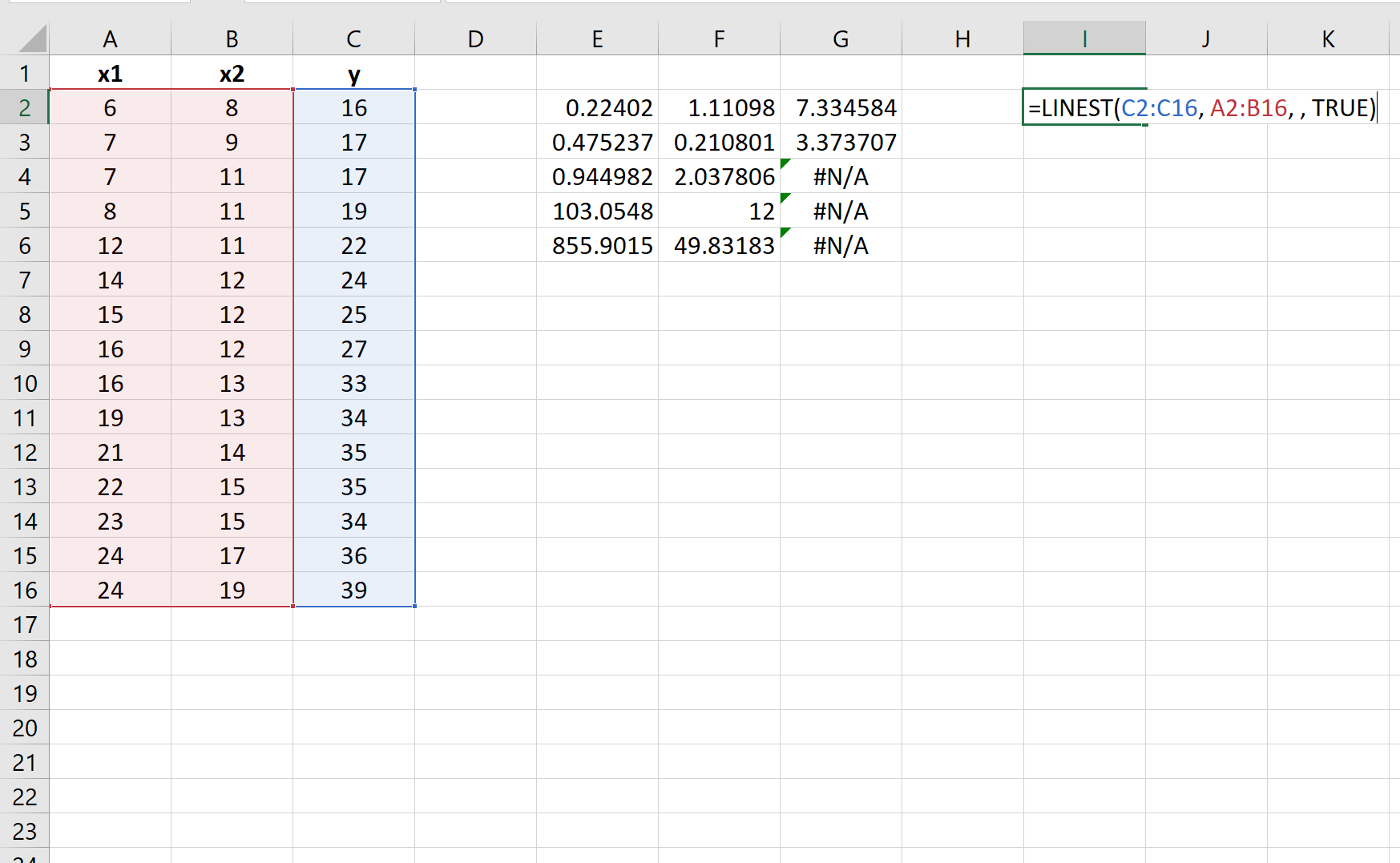
Залишкова сума квадратів для цієї моделі множинної лінійної регресії дорівнює 49,83 .

Додаткові ресурси

Як виконати просту лінійну регресію в Excel
Як виконати множинну лінійну регресію в Excel
Калькулятор залишкової суми квадратів