Що таке залишки в статистиці?

Залишок — це різниця між спостережуваним значенням і прогнозованим значенням у регресійному аналізі .

Він розраховується таким чином:

Залишок = спостережуване значення – прогнозоване значення

Пам’ятайте, що метою лінійної регресії є кількісна оцінка зв’язку між однією або кількома змінними предикторами та змінною відповіді . Для цього лінійна регресія знаходить лінію, яка найкраще «відповідає» даним, називається лінією регресії найменших квадратів .

Цей рядок створює прогноз для кожного спостереження в наборі даних, але малоймовірно, що прогноз, зроблений лінією регресії, точно відповідатиме спостережуваному значенню.

Різниця між прогнозованим і спостережуваним значенням є залишком. Якщо ми побудуємо спостережувані значення та накладемо підібрану лінію регресії, залишки для кожного спостереження будуть вертикальною відстанню між спостереженням і лінією регресії:

Спостереження має позитивний залишок, якщо його значення більше, ніж прогнозоване значення, зроблене лінією регресії.

І навпаки, спостереження має негативний залишок, якщо його значення менше, ніж прогнозоване значення, зроблене лінією регресії.

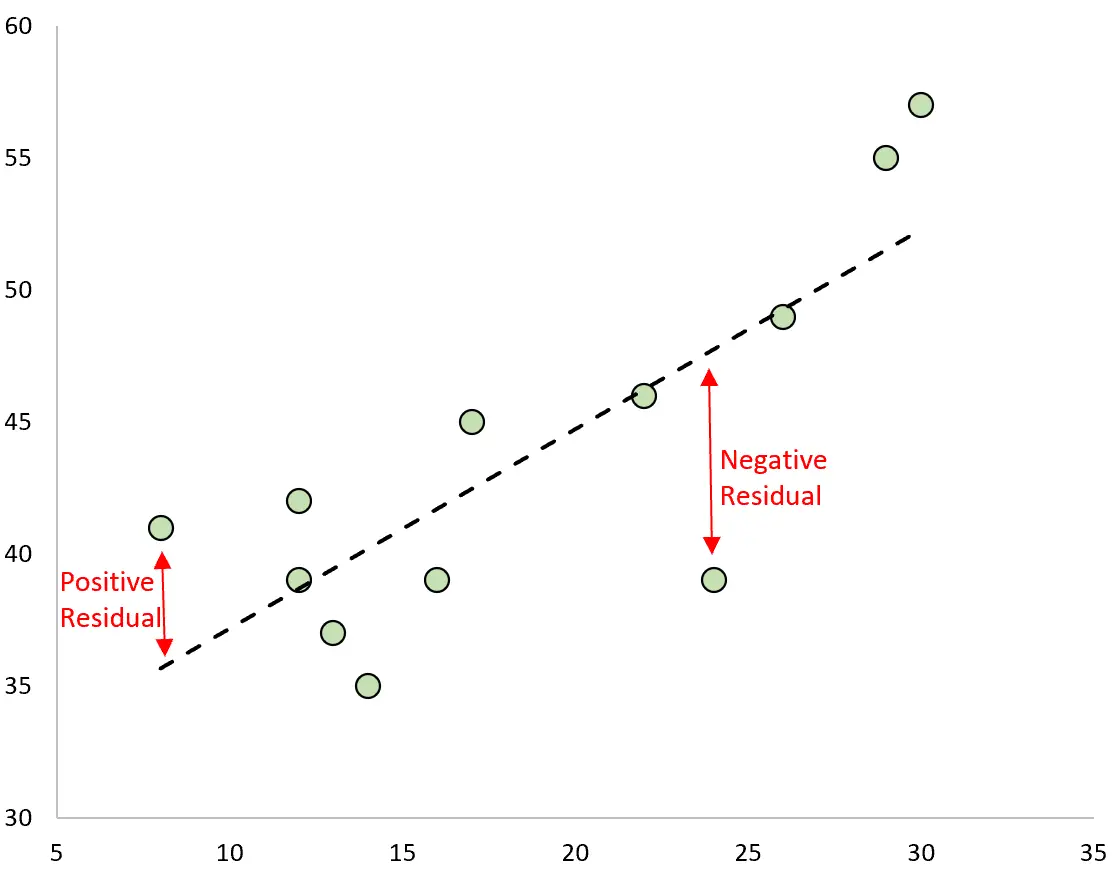
Деякі спостереження матимуть позитивні залишки, тоді як інші матимуть негативні залишки, але всі залишки складатимуть нуль .

Приклад розрахунку залишків

Припустімо, що ми маємо наступний набір даних із загалом 12 спостереженнями:

Якщо ми використовуємо статистичне програмне забезпечення (наприклад, R , Excel , Python , Stata тощо), щоб підібрати лінію лінійної регресії до цього набору даних, ми виявимо, що найкраща лінія виявиться:

y = 29,63 + 0,7553x

Використовуючи цей рядок, ми можемо обчислити прогнозоване значення для кожного значення Y на основі значення X. Наприклад, прогнозоване значення першого спостереження буде таким:

y = 29,63 + 0,7553*(8) = 35,67

Тоді ми можемо обчислити нев’язку для цього спостереження наступним чином:

Залишок = спостережуване значення – прогнозоване значення = 41 – 35,67 = 5,33

Ми можемо повторити цей процес, щоб знайти нев’язку для кожного спостереження:

Якщо ми створимо діаграму розсіювання для візуалізації спостережень за допомогою підігнаної лінії регресії, ми побачимо, що деякі спостереження лежать над лінією, а інші лежать під нею:

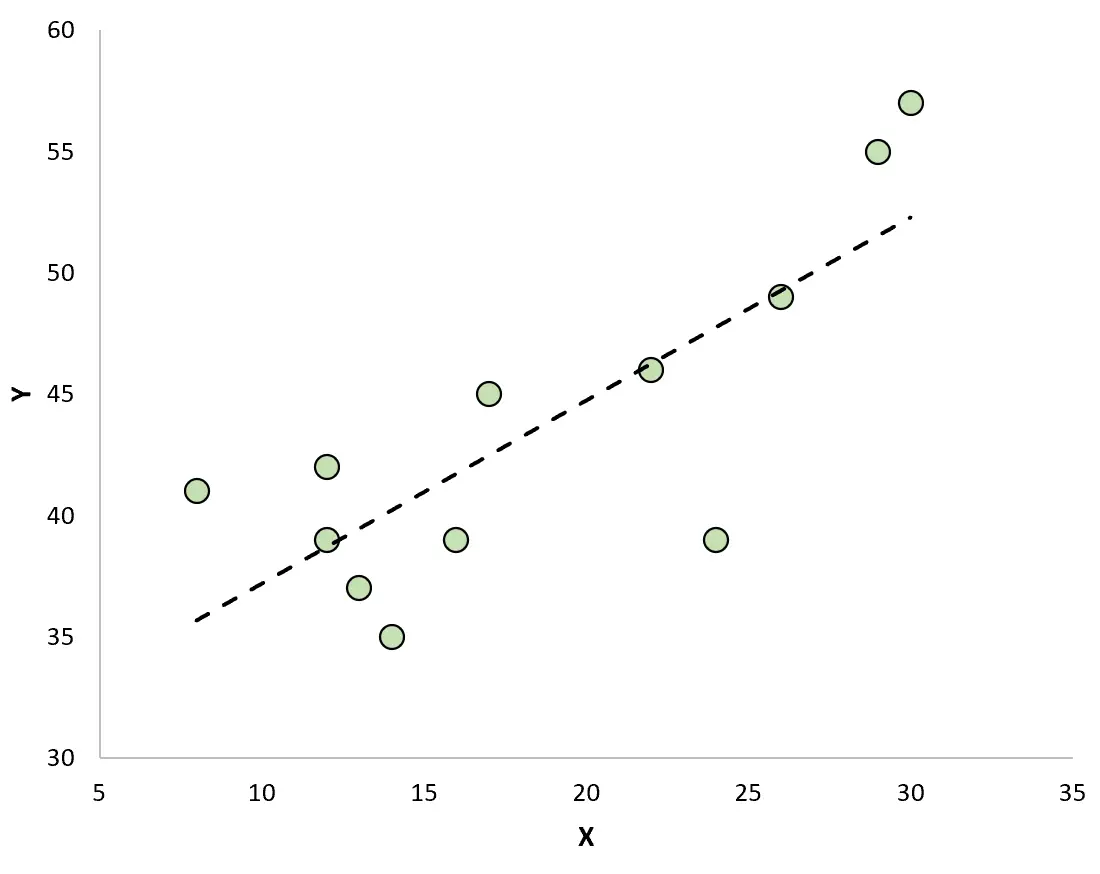
Властивості залишків

Залишки мають такі властивості:

• Кожне спостереження в наборі даних має відповідний залишок. Таким чином, якщо набір даних містить загалом 100 спостережень, модель створить 100 прогнозованих значень, у результаті чого загалом буде 100 залишків.
• Сума всіх залишків дорівнює нулю.
• Середнє значення залишків дорівнює нулю.

Як залишки використовуються на практиці?

На практиці залишки використовуються в регресії з трьох різних причин:

1. Оцінити адекватність моделі.

Коли ми створили підігнану лінію регресії, ми можемо обчислити залишкову суму квадратів (RSS) , яка є сумою всіх квадратів залишків. Чим нижчий RSS, тим краще модель регресії відповідає даним.

2. Перевірте припущення про нормальність.

Одним із ключових припущень лінійної регресії є те, що залишки мають нормальний розподіл.

Щоб перевірити цю гіпотезу, ми можемо створити графік QQ, який є типом графіка, який ми можемо використовувати, щоб визначити, чи слідують залишки моделі нормальному розподілу.

Якщо точки на графіку приблизно утворюють пряму діагональну лінію, тоді виконується припущення нормальності.

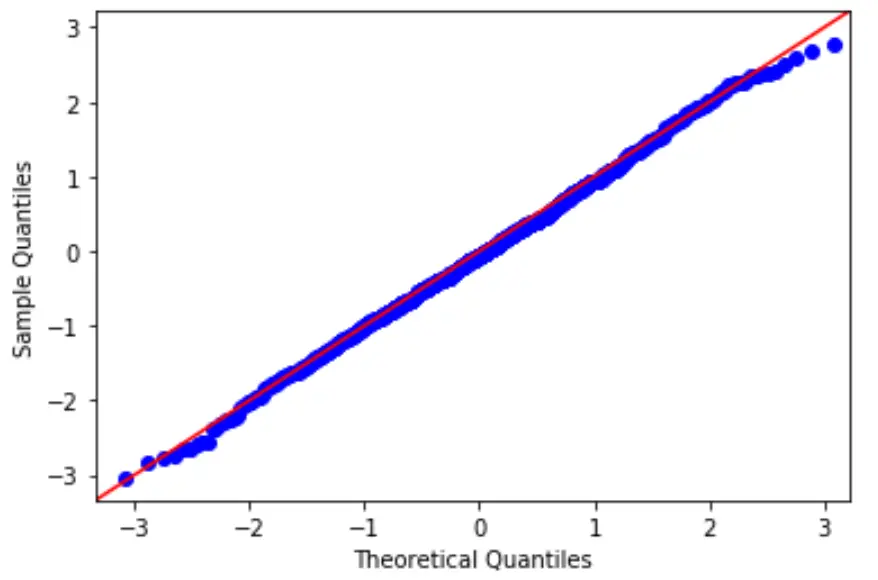
3. Перевірте припущення гомоскедастичності.

Іншим ключовим припущенням лінійної регресії є те, що залишки мають постійну дисперсію на кожному рівні x. Це називається гомоскедастичністю. Коли це не так, залишки страждають від гетероскедастичності .

Щоб перевірити, чи виконується це припущення, ми можемо створити графік залишків , який є діаграмою розсіювання, яка показує залишки порівняно з прогнозованими значеннями моделі.

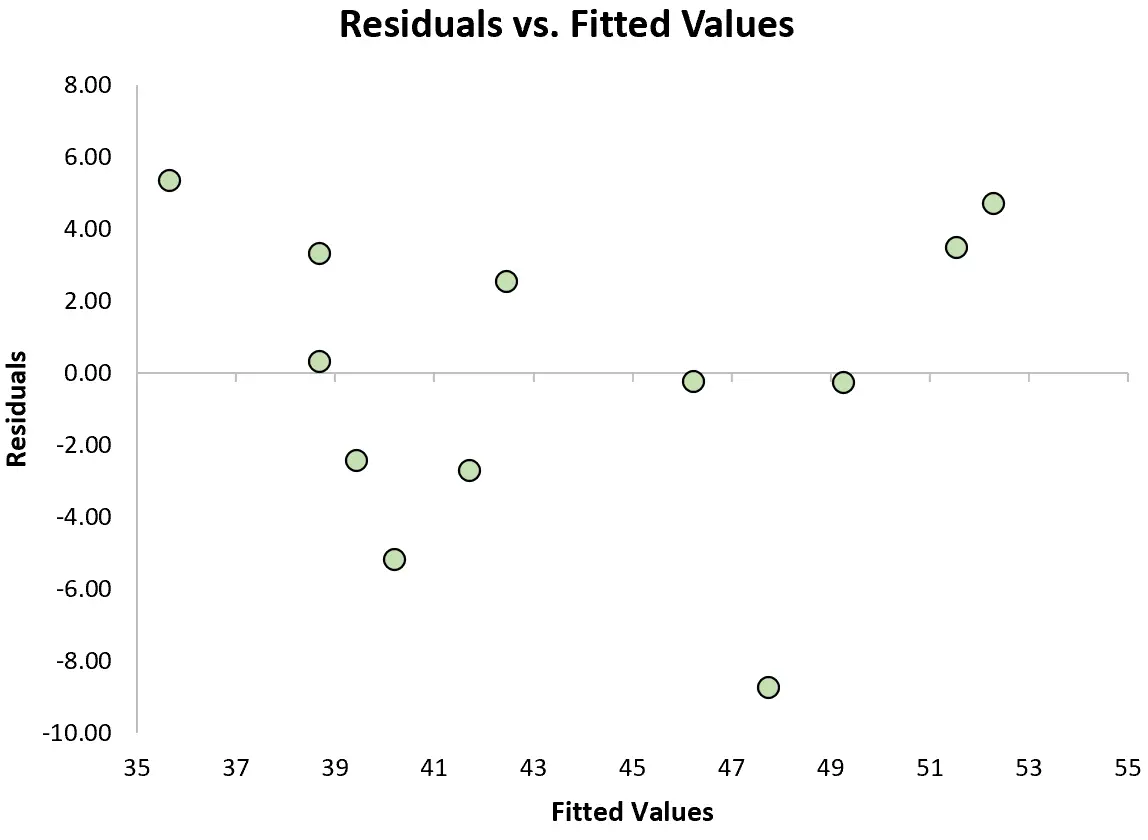
Якщо залишки приблизно рівномірно розподілені навколо нуля на графіку без чіткої тенденції, ми загалом говоримо, що припущення про гомоскедастичність виконується.

Додаткові ресурси

Вступ до простої лінійної регресії
Вступ до множинної лінійної регресії
Чотири припущення лінійної регресії
Як створити діаграму залишку в Excel