Зворотний нормальний розподіл: визначення та приклад

Термін зворотний нормальний розподіл стосується методу використання відомої ймовірності для знаходження відповідного z-критичного значення в нормальному розподілі .

Це не слід плутати з оберненим розподілом Гауса , який є безперервним розподілом ймовірностей.

У цьому підручнику наведено декілька прикладів використання зворотного нормального розподілу в різних статистичних програмах.

Зворотний нормальний розподіл маємо калькулятор TI-83 або TI-84

Найімовірніше, ви зустрінете термін «обернений нормальний розподіл» на калькуляторі TI-83 або TI-84, який використовує таку функцію для знаходження критичного значення z, яке відповідає певній ймовірності:

invNorm(імовірність, μ, σ)

золото:

• ймовірність: рівень значущості
• μ: середня популяція
• σ: стандартне відхилення сукупності

Ви можете отримати доступ до цієї функції на калькуляторі TI-84, натиснувши 2nd, а потім натиснувши vars . Це приведе вас до екрана DISTR , де ви зможете використовувати invNorm() :

Наприклад, ми можемо використовувати цю функцію, щоб знайти z-критичне значення, яке відповідає значенню ймовірності 0,05:

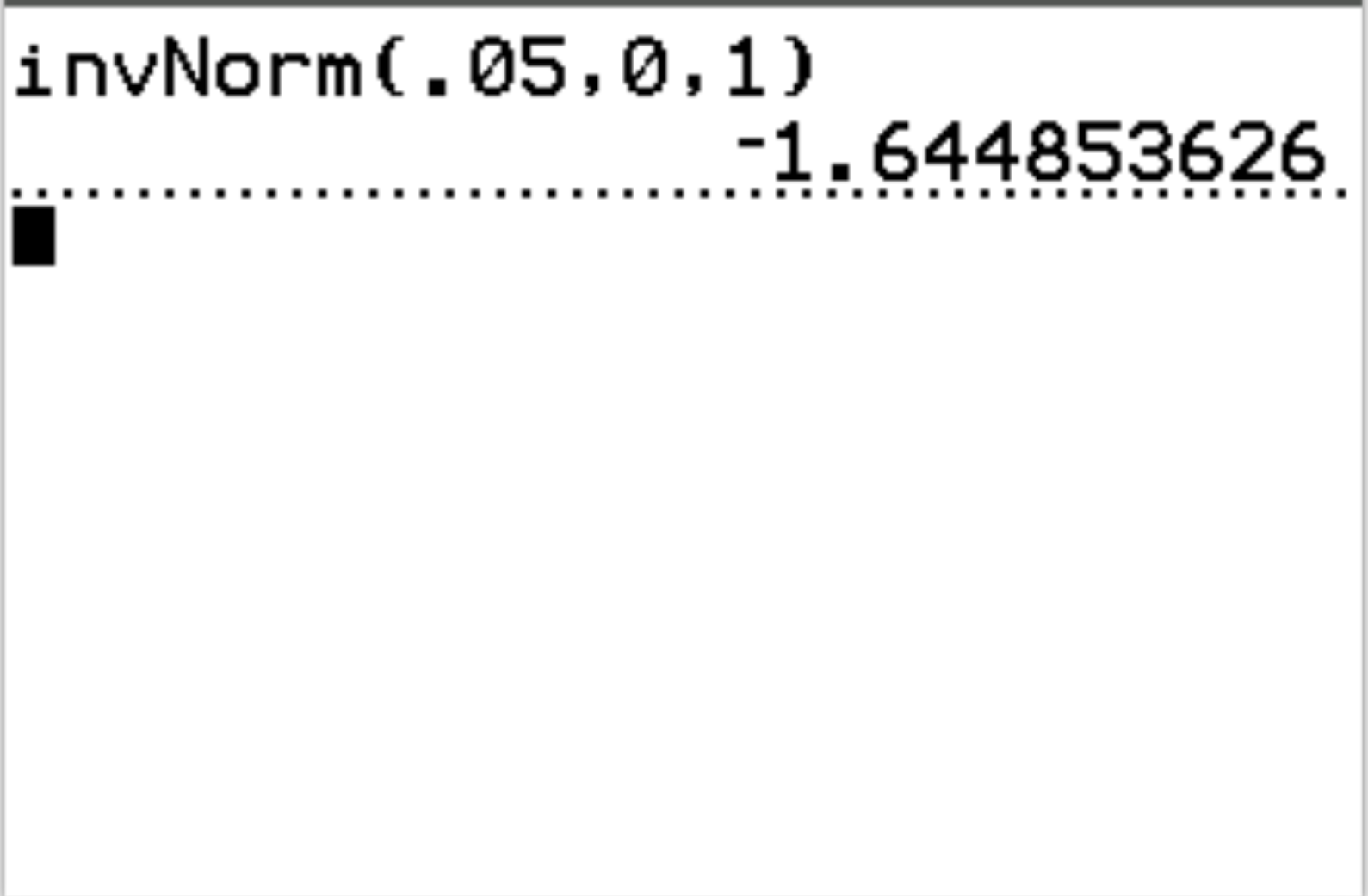
Критичне значення z, яке відповідає значенню ймовірності 0,05, становить -1,64485 .

Пов’язане: Як використовувати invNorm на калькуляторі TI-84 (з прикладами)

Зворотний нормальний розподіл в Excel

Щоб знайти z-критичне значення, пов’язане з певним значенням імовірності в Excel, ми можемо скористатися функцією INVNORM() , яка використовує такий синтаксис:

INVNORM(p, середнє, sd)

золото:

• p: рівень значущості
• середнє: середнє населення
• sd: стандартне відхилення сукупності

Наприклад, ми можемо використовувати цю функцію, щоб знайти z-критичне значення, яке відповідає значенню ймовірності 0,05:

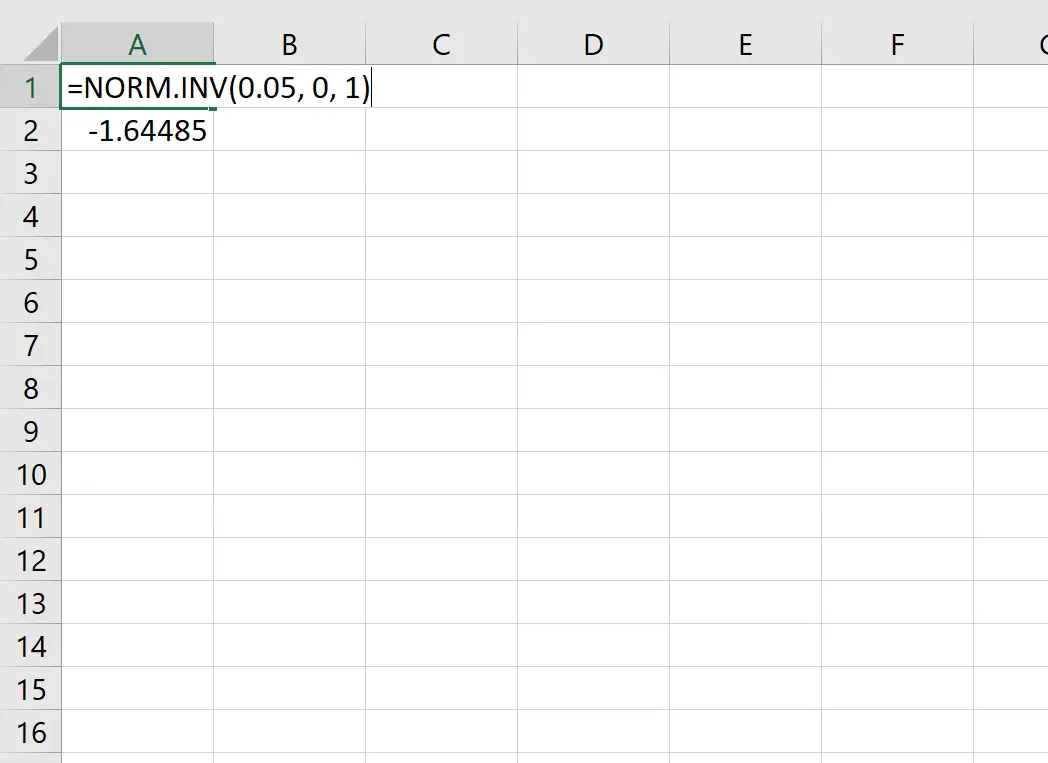
Критичне значення z, яке відповідає значенню ймовірності 0,05, становить -1,64485 .

Зворотний нормальний розподіл в R

Щоб знайти z-критичне значення, пов’язане з певним значенням імовірності в R, ми можемо використати функцію qnorm() , яка використовує такий синтаксис:

qнорма (p, середнє значення, sd)

золото:

• p: рівень значущості
• середнє: середнє населення
• sd: стандартне відхилення сукупності

Наприклад, ми можемо використовувати цю функцію, щоб знайти z-критичне значення, яке відповідає значенню ймовірності 0,05:

 qnorm (p= .05 , mean= 0 , sd= 1 )

[1] -1.644854

Знову ж таки, критичне z-значення, яке відповідає значенню ймовірності 0,05, становить -1,64485 .