Як знайти ймовірність за середнім значенням і стандартним відхиленням

Ми можемо використати наступний процес, щоб знайти ймовірність того, що випадкова змінна з нормальним розподілом

Крок 1. Знайдіть z-оцінку.

Z-показник показує, на скільки стандартних відхилень окреме значення даних падає від середнього. Він розраховується таким чином:

z-оцінка = (x – μ) / σ

золото:

• x: індивідуальне значення даних
• μ: середня популяція
• σ: стандартне відхилення сукупності

Крок 2: Знайти ймовірність, яка відповідає z-показнику.

Коли ми обчислили z-оцінку, ми можемо знайти відповідну ймовірність у z-таблиці.

У наведених нижче прикладах показано, як використовувати цей процес у різних сценаріях.

Приклад 1: Імовірність менше певного значення

Оцінки за певний тест зазвичай розподіляються із середнім значенням μ = 82 і стандартним відхиленням σ = 8. Яка ймовірність того, що даний учень набере менше 84 балів за тест?

Крок 1. Знайдіть z-оцінку.

Спочатку ми знайдемо z-оцінку, пов’язану з оцінкою 84:

z-оцінка = (x – μ) / σ = (84 – 82) / 8 = 2/8 = 0,25

Крок 2. Використовуйте таблицю z, щоб знайти відповідну ймовірність.

Далі ми шукатимемо значення 0,25 у таблиці z:

Ймовірність того, що даний студент отримає менше 84 балів, становить приблизно 59,87% .

Приклад 2: Імовірність перевищує певне значення

Зріст певного виду пінгвінів зазвичай розподіляється із середнім значенням μ = 30 дюймів і стандартним відхиленням σ = 4 дюйми. Якщо ми навмання виберемо пінгвіна, яка ймовірність того, що його зріст буде більше 28 дюймів?

Крок 1. Знайдіть z-оцінку.

Спочатку ми знайдемо z-показник, пов’язаний із зростом 28 дюймів.

Оцінка z = (x – μ) / σ = (28 – 30) / 4 = -2 / 4 = -0,5

Крок 2. Використовуйте таблицю z, щоб знайти відповідну ймовірність.

Далі ми шукатимемо значення -0,5   в таблиці z:

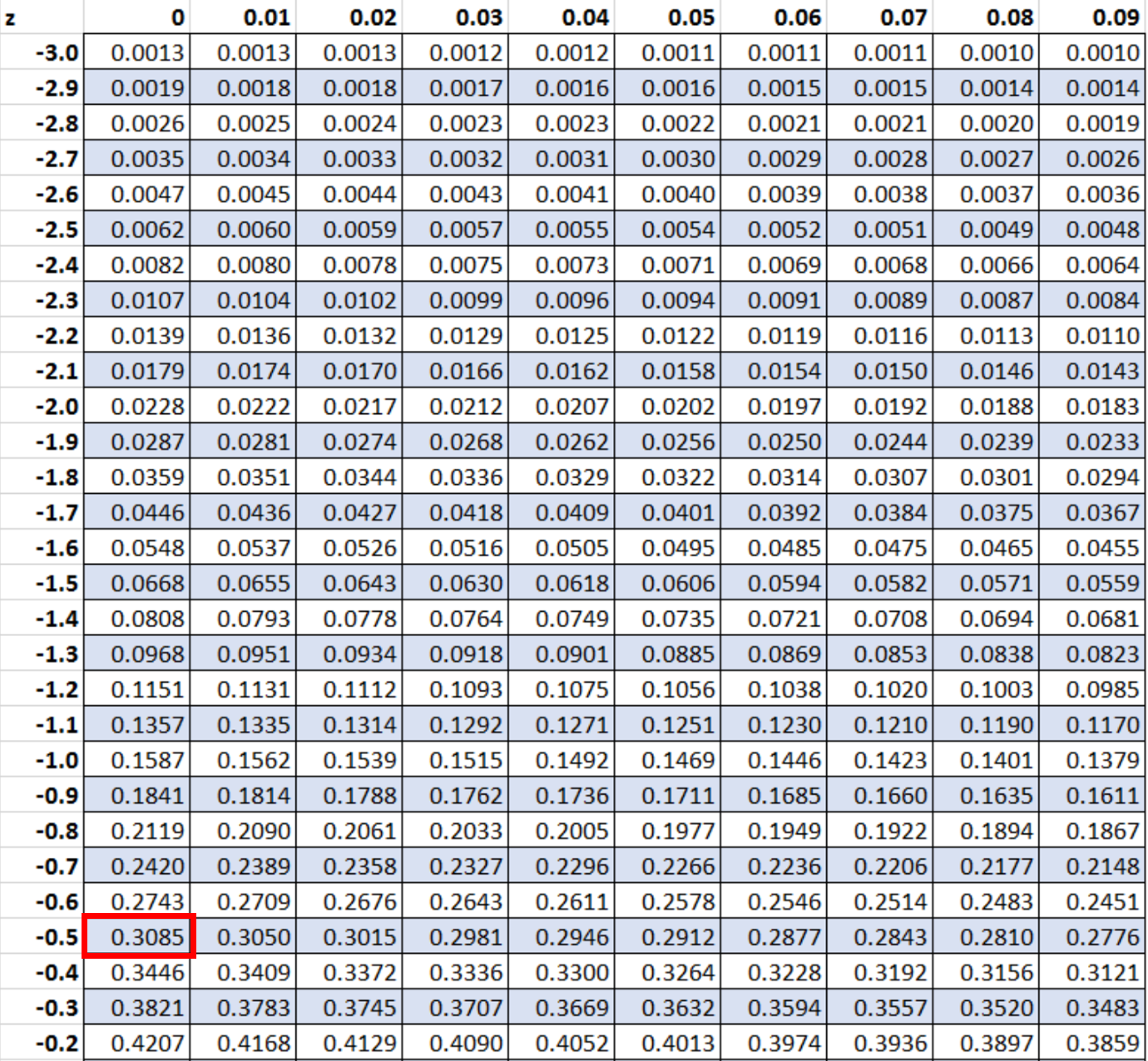
Значення, яке відповідає z-показнику -0,5, становить 0,3085. Це означає ймовірність того, що пінгвін буде меншим за 28 дюймів.

Однак, оскільки ми хочемо знати ймовірність того, що пінгвін вищий за 28 дюймів, нам потрібно відняти цю ймовірність від 1.

Отже, ймовірність того, що пінгвін вищий за 28 дюймів, становить: 1 – 0,3085 = 0,6915 .

Приклад 3: Імовірність між двома значеннями

Вага певного виду черепах зазвичай розподіляється із середнім значенням μ = 400 фунтів і стандартним відхиленням σ = 25 фунтів. Якщо ми навмання виберемо черепаху, яка ймовірність того, що вона важить від 410 до 425 фунтів?

Крок 1. Знайдіть z-оцінки.

По-перше, ми знайдемо z-показники, пов’язані з 410 та 425 книгами

z-оцінка 410 = (x – μ) / σ = (410 – 400) / 25 = 10/25 = 0,4

z оцінка 425 = (x – μ) / σ = (425 – 400) / 25 = 25 / 25 = 1

Крок 2. Використовуйте таблицю z, щоб знайти відповідну ймовірність.

Спочатку ми шукатимемо значення 0,4   в таблиці z:

Далі ми шукатимемо значення 1   в таблиці z:

Далі ми віднімемо менше значення від більшого значення: 0,8413 – 0,6554 = 0,1859 .

Таким чином, ймовірність того, що навмання обрана черепаха важить від 410 фунтів до 425 фунтів, становить 18,59% .

Додаткові ресурси

Як вручну обчислити значення P на основі Z-оцінки
Як конвертувати бали Z у необроблені бали
Як знайти Z бали в певній області