Тау кендалла: визначення + приклад
У статистиці кореляція означає силу та напрямок зв’язку між двома змінними. Значення коефіцієнта кореляції може коливатися від -1 до 1, де -1 вказує на ідеальний негативний зв’язок, 0 вказує на відсутність зв’язку, а 1 вказує на ідеальний позитивний зв’язок.
Найбільш часто використовуваним коефіцієнтом кореляції є коефіцієнт кореляції Пірсона , який вимірює лінійний зв’язок між двома числовими змінними.
Рідше використовуваним коефіцієнтом кореляції є тау Кендалла , який вимірює зв’язок між двома стовпцями ранжованих даних.
Формула для обчислення тау Кендалла, часто скорочено τ, така:
τ = (CD) / (C+D)
золото:
C = кількість відповідних пар
D = кількість дискордантних пар
У наступному прикладі показано, як використовувати цю формулу для обчислення коефіцієнта рангової кореляції Kendall Tau для двох стовпців ранжованих даних.
Приклад розрахунку тау Кендалла
Припускається, що два баскетбольні тренери ранжують 12 своїх гравців від гіршого до найкращого. У наступній таблиці показано рейтинги, які кожен тренер присвоїв гравцям:
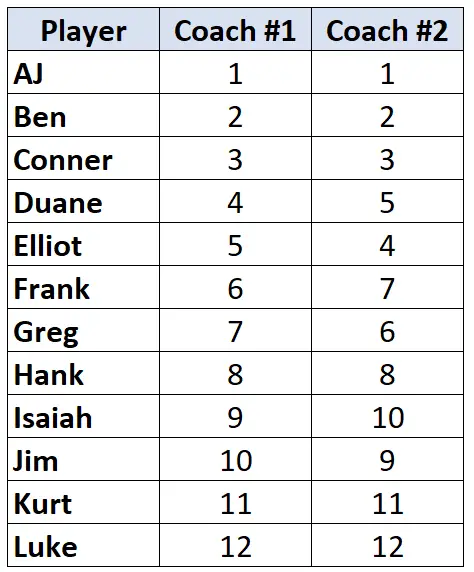
Оскільки ми працюємо з двома стовпцями ранжованих даних, доцільно використовувати тау Кендалла для розрахунку кореляції між рейтингами двох тренерів. Щоб обчислити тау Кендалла, виконайте такі дії:
Крок 1: підрахуйте кількість відповідних пар.
Подивіться лише на рейтинги тренера №2. Починаючи з першого гравця, порахуйте, на скільки рангів нижче нього вищі . Наприклад, під «1» є 11 чисел, які є більшими, тому ми напишемо 11:
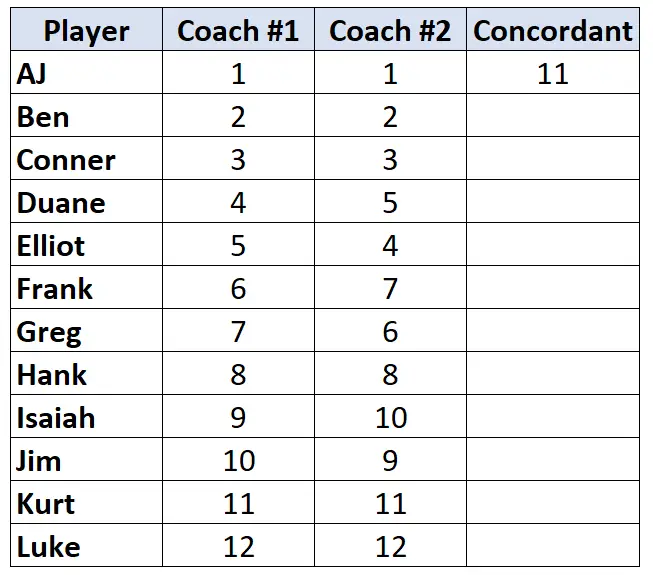
Перейдіть до наступного гравця та повторіть процес. Є 10 чисел під «2», які є більшими, тому ми напишемо 10:
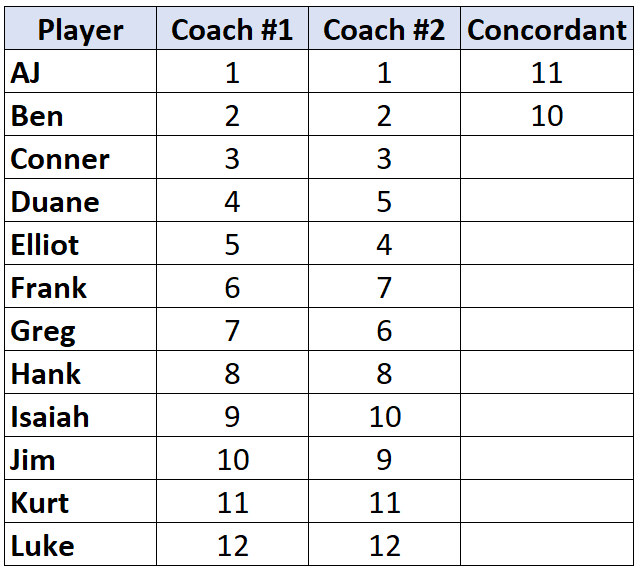
Коли ми досягаємо гравця, чий ранг нижчий , ніж гравець до нього, йому просто призначається таке ж значення, як і гравець до нього. Наприклад, Елліот має ранг «4», який нижчий за ранг попереднього гравця «5», тому йому просто присвоюється таке ж значення, як і гравцеві до нього:
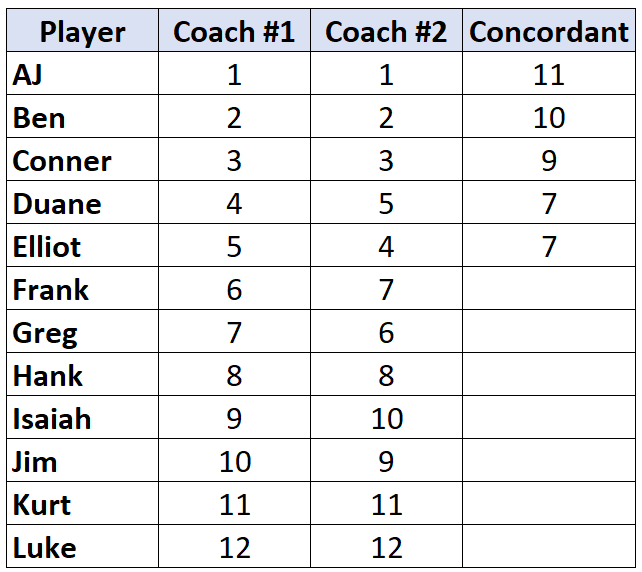
Повторіть цей процес для всіх гравців:
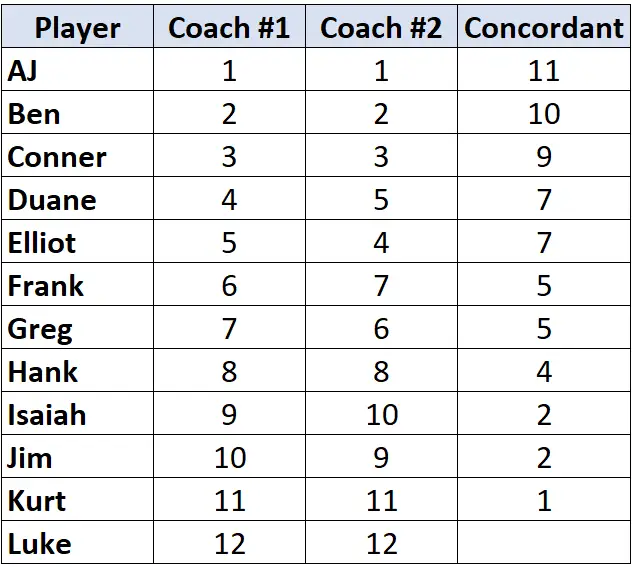
Крок 2: Підрахуйте кількість неузгоджених пар.
Знову ж таки, подивіться лише на рейтинг Тренера №2. Для кожного гравця підрахуйте, скільки рангів нижче нього чи неї менше . Наприклад, тренер №2 присвоїв AJ ранг «1», і жоден гравець нижче його не має нижчого рангу. Таким чином, ми присвоюємо йому значення 0:
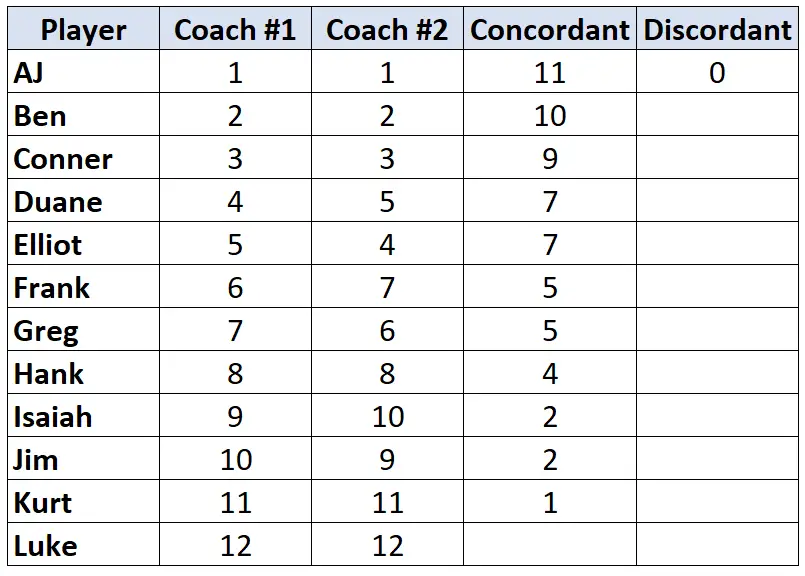
Повторіть цей процес для кожного гравця:
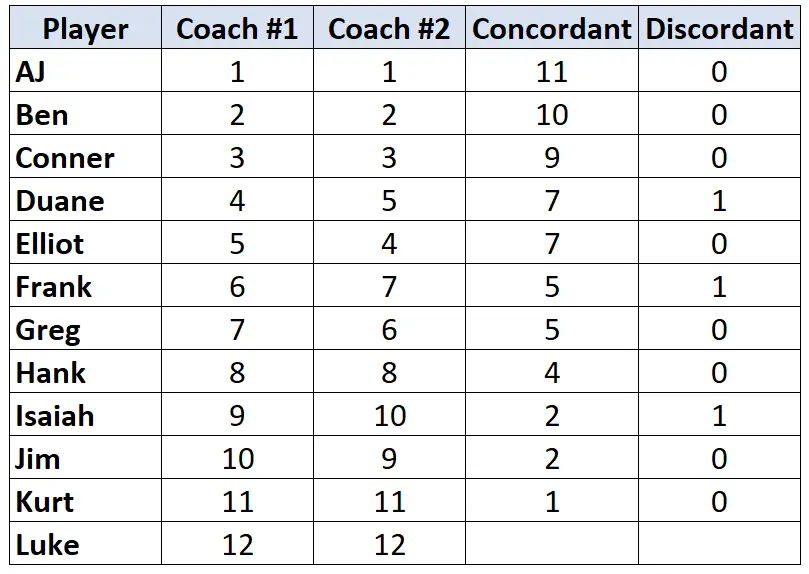
Крок 3: обчисліть суму кожного стовпця та знайдіть тау Кендалла.
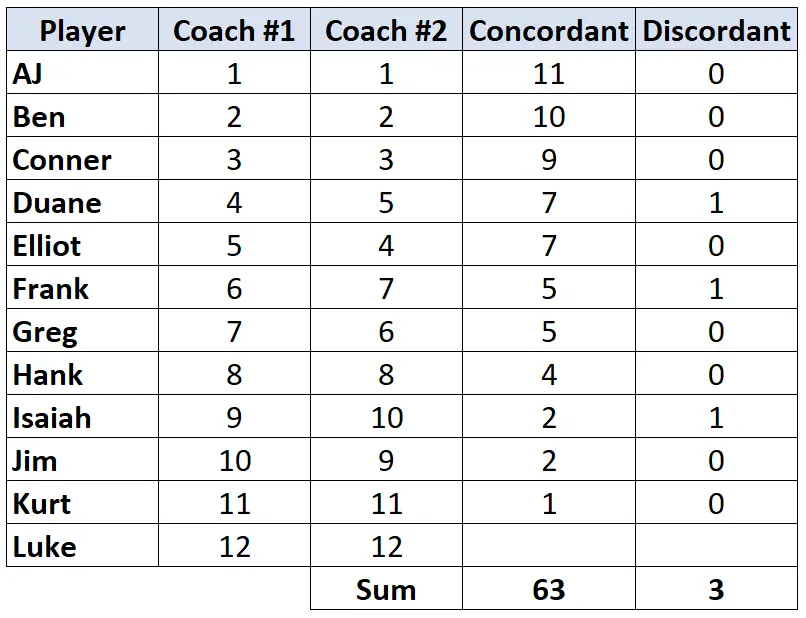
Тау Кендалла = (CD) / (C+D) = (63-3) / (63+3) = (60/66) = 0,909 .
Статистична важливість тау Кендалла
Якщо у вас більше n=10 пар, тау Кендалла зазвичай має нормальний розподіл. Щоб обчислити z-показник для тау Кендалла, можна використати наступну формулу:
z = 3τ*√ n(n-1) / √ 2(2n+5)
золото:
τ = значення, яке ви розрахували для тау Кендалла
n = кількість пар
Ось як обчислити z для попереднього прикладу:
z = 3(0,909)*√ 12(12-1) / √ 2(2*12+5) = 4,11 .
Використовуючи калькулятор Z-показника P-значення, ми бачимо, що значення p для цього z-показника становить 0,00004 , що є статистично значущим на рівні 0,05 альфа. Таким чином, існує статистично значуща кореляція між рангами, які обидва тренери присвоїли гравцям.
Бонус: як розрахувати тау Кендалла в R
У статистичному програмному забезпеченні R ви можете використовувати функцію kendall.tau() із бібліотеки VGAM для обчислення тау Кендалла для двох векторів, яка використовує такий синтаксис:
kendall.tau(x, y)
де x і y — два цифрові вектори однакової довжини.
Наступний код ілюструє, як обчислити тау Кендалла для точних даних, які ми використовували в попередньому прикладі:
#load VGAM library(VGAM) #create vector for each coach's rankings coach_1 <- c(1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12) coach_2 <- c(1, 2, 3, 5, 4, 7, 6, 8, 10, 9, 11, 12) #calculate Kendall's Tau kendall.tau(coach_1, coach_2) #[1] 0.9090909
Зверніть увагу, як значення Tau Кендалла відповідає значенню, яке ми обчислили вручну.