Колективно вичерпні події: визначення та приклад
Набір подій є сукупно вичерпним , якщо очікується , що відбудеться принаймні одна з подій.
Наприклад, якщо ми кидаємо кубик, він повинен впасти на одне з таких значень:
- 1
- 2
- 3
- 4
- 5
- 6
Таким чином, ми б сказали, що набір подій {1, 2, 3, 4, 5, 6} у сукупності є вичерпним , оскільки кубик має впасти на одне з цих значень.
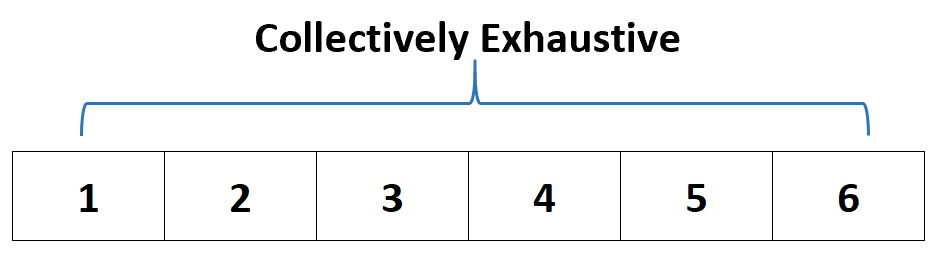
Іншими словами, цей набір подій, як сукупність , вичерпує всі можливі результати.
Наступні приклади показують інші ситуації, які ілюструють сукупно вичерпні події:
Приклад 1: підкинути монету
Припустимо, ми один раз кидаємо монету. Ми знаємо, що монета повинна впасти на одне з наступних значень:
- Голови
- Хвости
Таким чином, сукупність подій {Head, Tail} буде вичерпною.
Приклад 2: обертання волчка
Припустимо, у нас є колесо рулетки, яке має три різні кольори: червоний, синій і зелений.
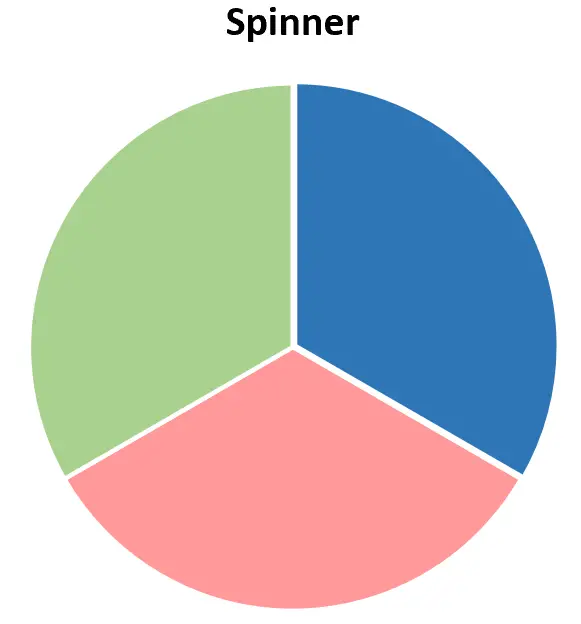
Якщо ми обертаємо його один раз, він повинен мати одне з таких значень:
- Червоний
- Синій
- Зелений
Таким чином, набір подій {Червоний, Синій, Зелений} у сукупності буде вичерпним.
Однак набір подій {Червоний, Зелений} не буде сукупно вичерпним, оскільки він не містить усіх можливих результатів.
Приклад 3: Типи баскетболістів
Припустімо, що у нас є опитування, яке пропонує людям вибрати бажану позицію в баскетболі. Єдині можливі відповіді:
- Керівник гри
- атакуючий захисник
- Маленький вперед
- Сила вперед
- центр
Таким чином, набір подій {розігруючий захисник, атакуючий захисник, маленький форвард, силовий форвард, центр} буде в сукупності вичерпним.
Проте набір подій {розігруючий захисник, атакуючий захисник, малий форвард} разом не буде вичерпним, оскільки він не містить усіх можливих результатів.
Важливість колективно вичерпних подій в опитуваннях
Під час розробки опитувань особливо важливо, щоб відповіді на запитання були комплексними.
Наприклад, припустімо, що в опитуванні ставиться таке запитання:
Яка ваша улюблена баскетбольна позиція?
І припустімо, що можливі відповіді:
- Керівник гри
- атакуючий захисник
- Маленький вперед
- Сила вперед
Оскільки позицію Центру залишили осторонь, ці відповіді не є вичерпними.
Це означає, що той, хто віддає перевагу Центру як бажану посаду, повинен буде вибрати один із інших варіантів, тобто відповіді на опитування не відображатимуть справжні думки опитаних.
Колективно вичерпні або взаємовиключні
Події є взаємовиключними , якщо вони не можуть відбутися одночасно.
Наприклад, нехай подія A — це подія, коли кубик падає на парне число, а подія B — подія, коли кубик падає на непарне число.
Ми б визначили вибірковий простір для подій наступним чином:
- A = {2, 4, 6}
- B = {1, 3, 5}
Зауважте, що між двома вибірковими просторами немає перекриття, тобто вони є взаємовиключними. У сукупності вони також є вичерпними, оскільки разом вони здатні врахувати всі потенційні результати кидка кубика.
Однак припустімо, що ми визначаємо події A та події B наступним чином:
- A = {1, 2, 3, 4}
- B = {3, 4, 5, 6}
У цьому випадку між A і B є певне перекриття, тому вони не є взаємовиключними. Однак у поєднанні вони все ще можуть врахувати всі потенційні результати кидка кубика.
Це ілюструє важливий момент: набір подій може бути сукупно вичерпним, але не бути взаємовиключним .