Коли слід використовувати поліноміальну регресію?

Поліноміальна регресія – це техніка, яку ми можемо використати для підгонки регресійної моделі, коли зв’язок між змінною(ями) предиктора та змінною відповіді є нелінійним.

Модель поліноміальної регресії має такий вигляд:

Y = β ₀ ⁺ β ₁ X + β ₂ X ² + … + β _h

На практиці є три прості способи визначити, чи варто вам використовувати поліноміальну регресію проти простішої моделі, як-от лінійної регресії .

1. Створіть діаграму розсіювання змінної предиктора та змінної відповіді

Найпростіший спосіб визначити, чи варто вам використовувати поліноміальну регресію, — це створити просту діаграму розсіювання змінної-провісника та змінної відповіді.

Наприклад, скажімо, ми хочемо використати змінну предиктор «study hours» для прогнозування оцінки, яку студент отримає на випускному іспиті.

Перш ніж підбирати регресійну модель, ми можемо створити діаграму розсіювання вивчених годин із результатами іспитів. Припустимо, наша діаграма розсіювання виглядає так:

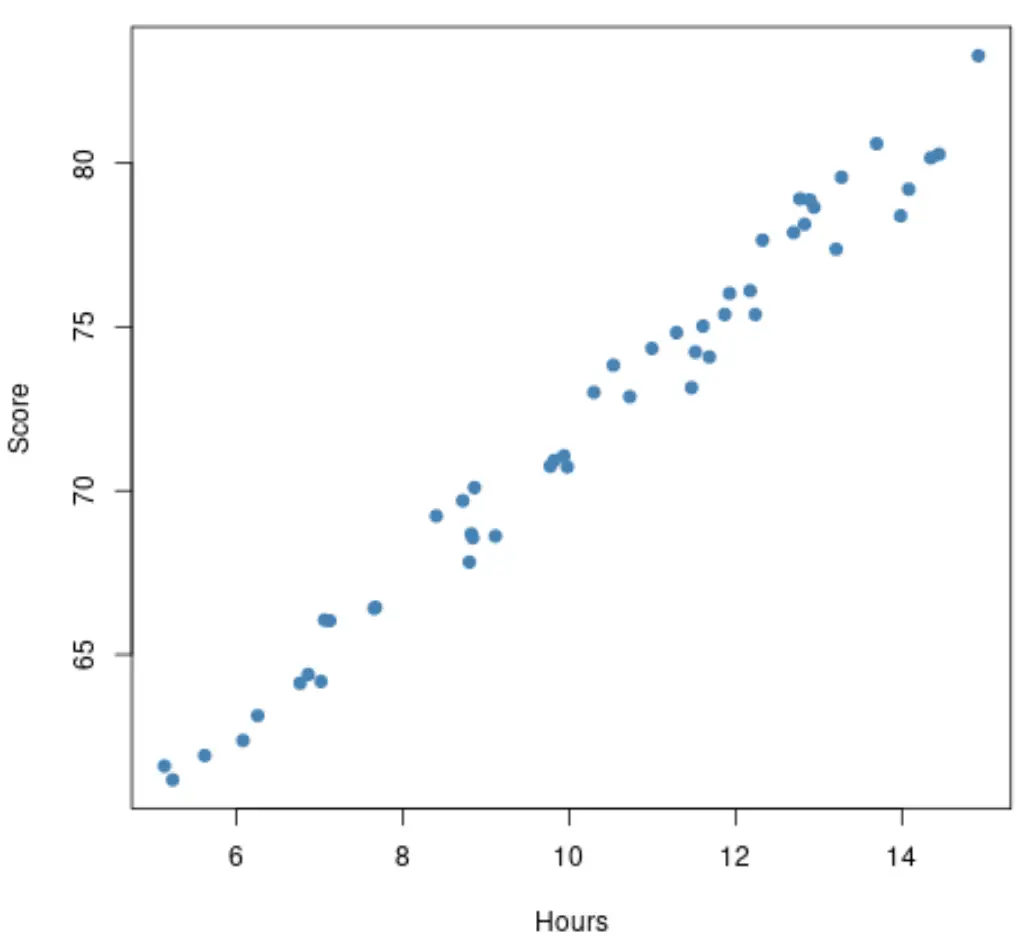
Зв’язок між вивченими годинами та результатами іспиту виглядає лінійним , тому було б доцільно підібрати просту модель лінійної регресії до цього набору даних.

Однак припустімо, що діаграма розсіювання насправді виглядає так:

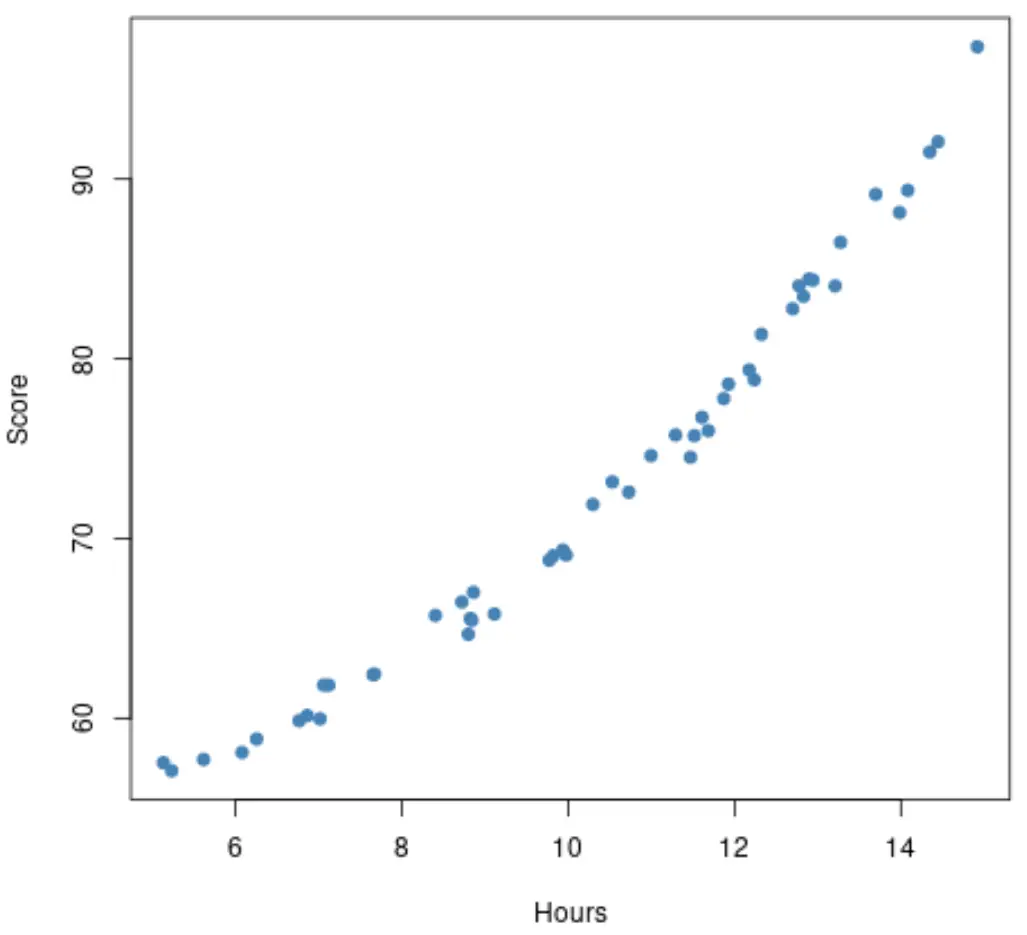
Цей зв’язок здається дещо більш нелінійним , що говорить нам про те, що було б доцільно застосувати натомість модель поліноміальної регресії.

2. Створіть графік підігнаних і залишкових значень

Інший спосіб визначити, чи варто вам використовувати поліноміальну регресію, — це підібрати модель лінійної регресії до набору даних, а потім створити графік підігнаних значень проти залишків для моделі.

Якщо існує чітка нелінійна тенденція в залишках, це означає, що поліноміальна регресія може забезпечити кращу відповідність даним.

Наприклад, припустімо, що ми підбираємо лінійну регресійну модель, використовуючи вивчені години як змінну прогностику та оцінку іспиту як змінну відповіді, а потім створюємо наступний графік підігнаних значень проти залишків:

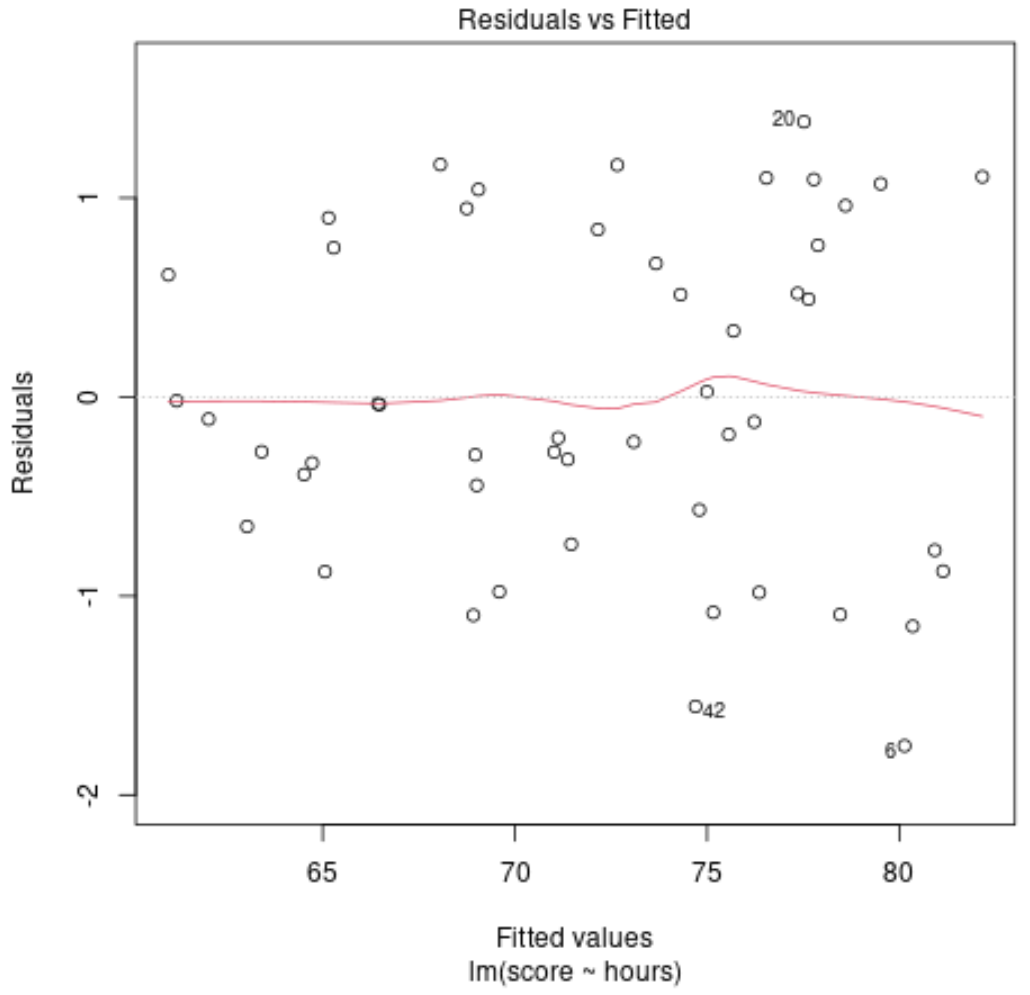
Залишки випадковим чином розкидані навколо нуля без чіткого шаблону, що вказує на те, що лінійна модель забезпечує належну підгонку до даних.

Однак давайте припустимо, що наш графік підігнаних значень проти залишків насправді виглядає так:

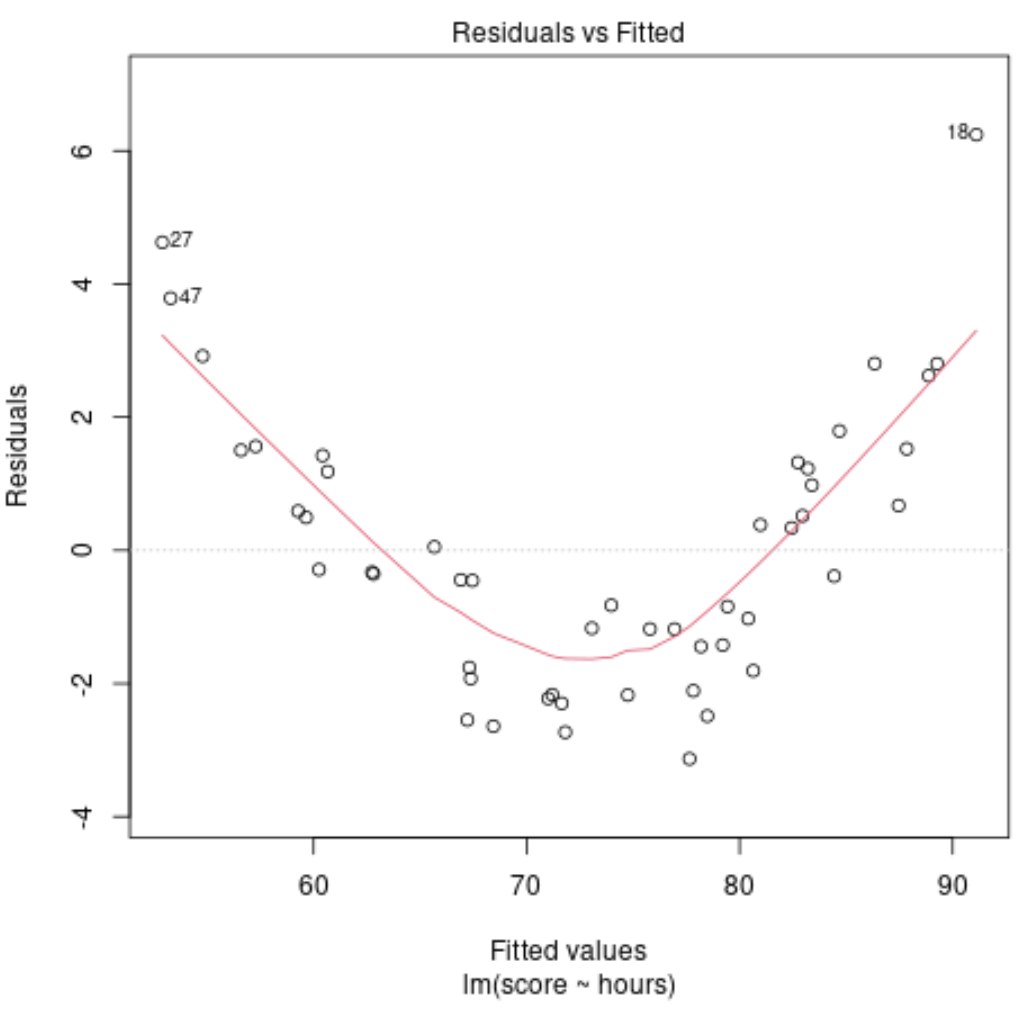
На графіку ми бачимо, що в залишках є чітка нелінійна картина – залишки мають форму «U».

Це говорить нам про те, що лінійна модель не підходить для цих конкретних даних і що було б доцільно підібрати замість неї модель поліноміальної регресії.

3. Обчисліть скориговане значення R-квадрат моделі

Інший спосіб визначити, чи варто вам використовувати поліноміальну регресію, полягає в підгонці моделі лінійної регресії та моделі поліноміальної регресії та обчисленні підігнаних значень R-квадрат для обох моделей.

Скоригований R-квадрат представляє частку дисперсії у змінній відповіді, яку можна пояснити змінними предикторів у моделі, скориговану на кількість змінних предикторів у моделі.

Модель з найвищим скоригованим R-квадратом представляє модель, яка найкраще може використовувати змінну(и) предиктора для пояснення варіації змінної відповіді.

Додаткові ресурси

У наступних посібниках пояснюється, як виконувати поліноміальну регресію за допомогою різного статистичного програмного забезпечення:

Вступ до поліноміальної регресії
Як виконати поліноміальну регресію в R
Як виконати поліноміальну регресію в Python
Як виконати поліноміальну регресію в Excel