Просте пояснення корекції безперервності в статистиці
Корекція безперервності застосовується, коли ви хочете використовувати неперервний розподіл для наближення дискретного розподілу. Зазвичай він використовується, коли потрібно використати нормальний розподіл для наближення біноміального розподілу .
Нагадаємо, що біноміальний розподіл говорить нам про ймовірність досягнення x успіху в n випробуваннях, враховуючи, що ймовірність успіху в одному випробуванні дорівнює p . Щоб відповісти на запитання про ймовірність за допомогою біноміального розподілу, ми могли б просто використати калькулятор біноміального розподілу , але ми також могли б наближено визначити ймовірність за допомогою нормального розподілу з поправкою на безперервність.
Поправка на безперервність – це назва, яку дають додаванню або відніманню 0,5 від дискретного значення x .
Наприклад, скажімо, ми хочемо знайти ймовірність того, що монета впаде на голови, що менше або дорівнює 45 разам протягом 100 підкидань. Тобто ми хочемо знайти P(X ≤ 45). Щоб використати нормальний розподіл для апроксимації біноміального розподілу, ми замість цього знайдемо P(X ≤ 45,5).
У наведеній нижче таблиці показано, коли потрібно додавати або віднімати 0,5 залежно від типу ймовірності, яку ви намагаєтеся знайти:
| Використовуйте біноміальний розподіл | Використання нормального розподілу з поправкою на безперервність |
|---|---|
| X = 45 | 44,5 < X < 45,5 |
| X ≤ 45 | X < 45,5 |
| X < 45 | X < 44,5 |
| X ≥ 45 | X > 44,5 |
| X > 45 | X > 45,5 |
Примітка:
Застосовувати корекцію безперервності до нормального розподілу, щоб наблизити біноміальний розподіл, доцільно лише тоді, коли обидва n*p і n*(1-p) дорівнюють принаймні 5.
Наприклад, припустимо, що n = 15 і p = 0,6. В цьому випадку:
n*p = 15 * 0,6 = 9
n*(1-p) = 15 * (1 – 0,6) = 15 * (0,4) = 6
Оскільки обидва ці числа більші або дорівнюють 5, у цьому сценарії було б прийнятно застосувати корекцію безперервності.
У наступному прикладі показано, як застосувати поправку на безперервність до нормального розподілу, щоб наблизити біноміальний розподіл.
Приклад застосування корекції безперервності
Припустімо, ми хочемо знати ймовірність того, що монета впаде на орди, що менше або дорівнює 43 разам у 100 підкиданнях. В цьому випадку:
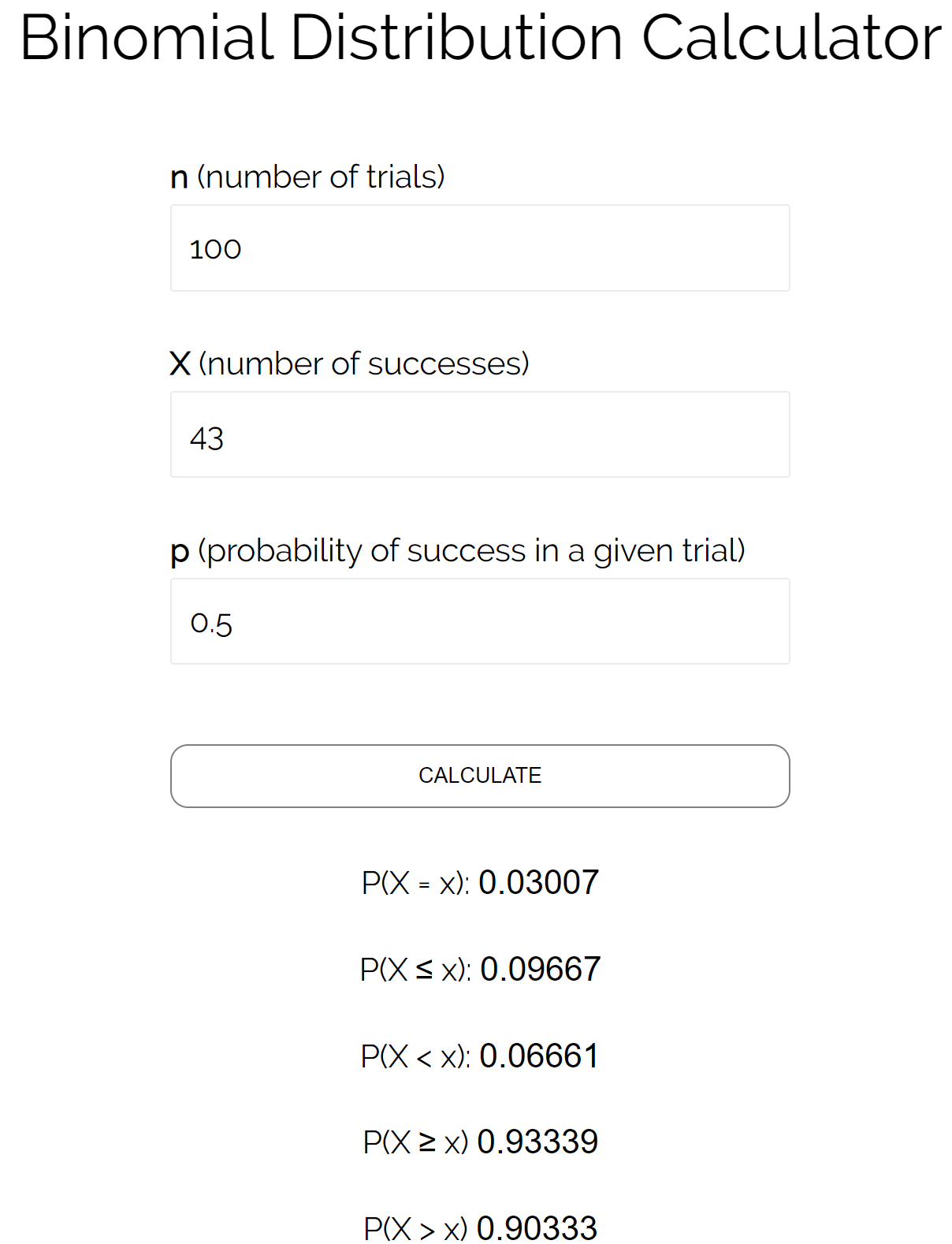
n = кількість випробувань = 100
X = кількість успіхів = 43
p = ймовірність успіху в даному дослідженні = 0,50
Ми можемо підключити ці числа до калькулятора біноміального розподілу , щоб побачити, що ймовірність того, що монета впаде на голови, що менше або дорівнює 43 разам, дорівнює 0,09667 .
Щоб наблизити біноміальний розподіл шляхом застосування поправки на безперервність до нормального розподілу, ми можемо використати наступні кроки:
Крок 1. Переконайтеся, що n*p і n*(1-p) обидва принаймні 5 .
n*p = 100*0,5 = 50
n*(1-p) = 100*(1 – 0,5) = 100*0,5 = 50
Обидва числа більші або дорівнюють 5, тому ми можемо продовжити.
Крок 2: Визначте, додавати чи віднімати 0,5
Посилаючись на таблицю вище, ми бачимо, що ми повинні додати 0,5 , коли ми працюємо з імовірністю у формі X ≤ 43. Таким чином, ми знайдемо P(X< 43,5).
Крок 3: Знайдіть середнє (μ) і стандартне відхилення (σ) біноміального розподілу.
µ = n*p = 100*0,5 = 50
σ = √ n*p*(1-p) = √ 100*.5*(1-.5) = √ 25 = 5
Крок 4. Знайдіть z-показник, використовуючи середнє значення та стандартне відхилення, знайдене на попередньому кроці.
z = (x – μ) / σ = (43,5 – 50) / 5 = -6,5 / 5 = -1,3.
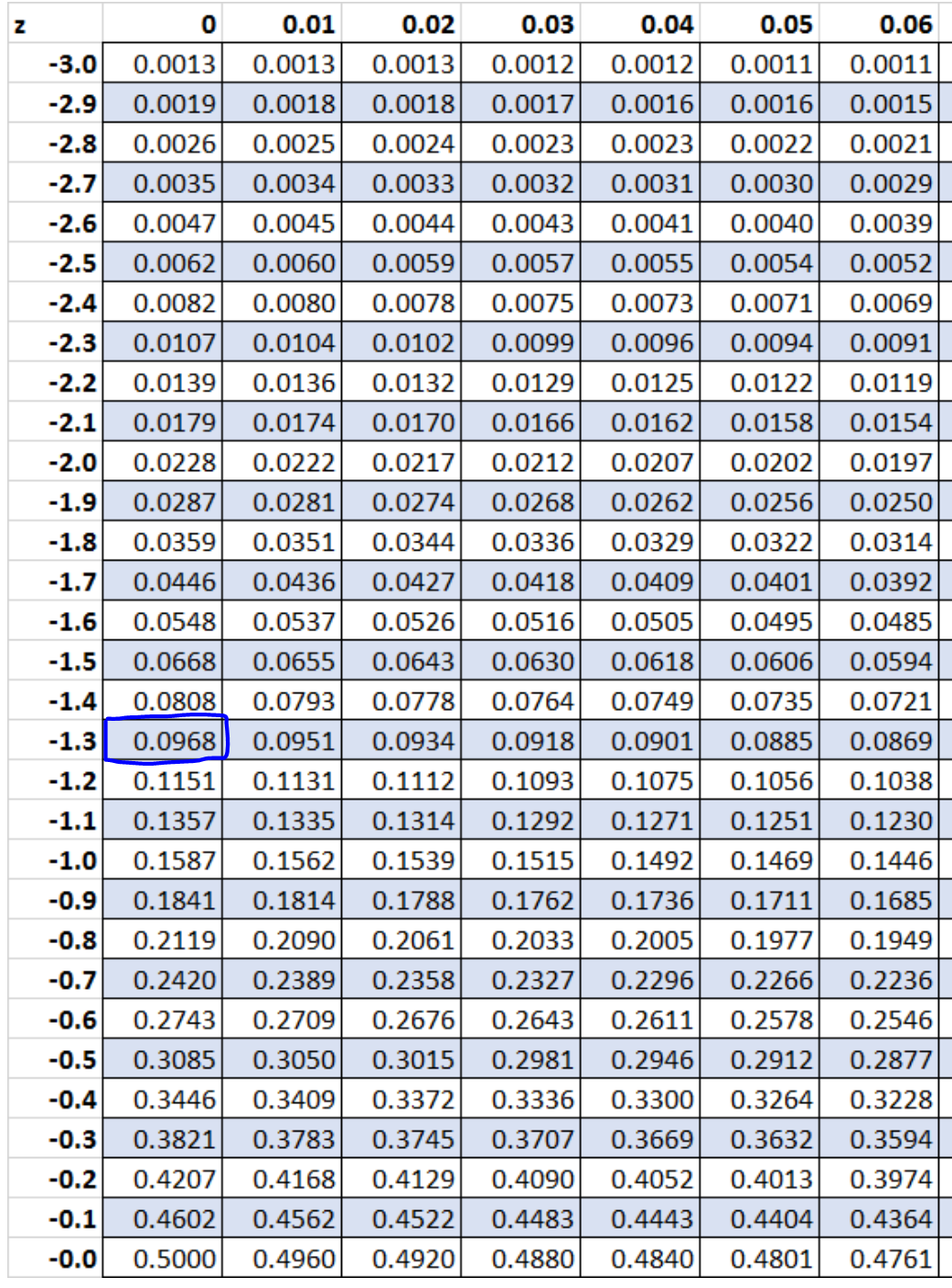
Крок 5. Використовуйте Z-таблицю, щоб знайти ймовірність, пов’язану з z-рахунком.
Згідно з таблицею Z, ймовірність, пов’язана з z = -1,3, становить 0,0968 .
Отже, точна ймовірність, яку ми знайшли за допомогою біноміального розподілу, становила 0,09667 , тоді як приблизна ймовірність, яку ми знайшли за допомогою корекції безперервності з нормальним розподілом, становила 0,0968 . Ці два значення досить замкнуті.
Коли використовувати корекцію безперервності
До появи сучасного статистичного програмного забезпечення і розрахунків доводилося робити вручну, поправки на безперервність часто використовувалися для визначення ймовірностей із застосуванням дискретних розподілів. Сьогодні поправки на безперервність відіграють меншу роль у розрахунку ймовірностей, оскільки зазвичай ми можемо покладатися на програмне забезпечення або калькулятори для розрахунку ймовірностей.
Натомість це просто тема, яка розглядається в курсах статистики, щоб проілюструвати взаємозв’язок між біноміальним розподілом і нормальним розподілом і показати, що нормальний розподіл може наближено до біноміального розподілу шляхом застосування поправки на безперервність.
Калькулятор корекції безперервності
Використовуйте калькулятор поправки на безперервність , щоб автоматично застосувати поправку на безперервність до нормального розподілу для наближення біноміальних ймовірностей.