Як створити кореляційну матрицю в python

Одним із способів кількісного визначення зв’язку між двома змінними є використання коефіцієнта кореляції Пірсона , який є мірою лінійного зв’язку між двома змінними .

Він приймає значення від -1 до 1, де:

• -1 вказує на абсолютно негативну лінійну кореляцію.
• 0 означає відсутність лінійної кореляції.
• 1 вказує на абсолютно позитивну лінійну кореляцію.

Чим далі коефіцієнт кореляції від нуля, тим сильніший зв’язок між двома змінними.

Але в деяких випадках ми хочемо зрозуміти кореляцію між кількома парами змінних. У цих випадках ми можемо створити кореляційну матрицю , яка є квадратною таблицею, що показує коефіцієнти кореляції між кількома попарними комбінаціями змінних.

Цей посібник пояснює, як створити та інтерпретувати кореляційну матрицю в Python.

Як створити кореляційну матрицю в Python

Виконайте наступні кроки, щоб створити кореляційну матрицю в Python.

Крок 1: Створіть набір даних.

 import pandas as pd

data = {'assists': [4, 5, 5, 6, 7, 8, 8, 10],
        'rebounds': [12, 14, 13, 7, 8, 8, 9, 13],
        'points': [22, 24, 26, 26, 29, 32, 20, 14]
        }

df = pd. DataFrame (data, columns=['assists','rebounds','points'])
df

   assist rebound points
0 4 12 22
1 5 14 24
2 5 13 26
3 6 7 26
4 7 8 29
5 8 8 32
6 8 9 20
7 10 13 14

Крок 2: Створіть кореляційну матрицю.

 #create correlation matrix
df. corr ()

                assists rebound points
assists 1.000000 -0.244861 -0.329573
rebounds -0.244861 1.000000 -0.522092
points -0.329573 -0.522092 1.000000

#create same correlation matrix with coefficients rounded to 3 decimals 
df. corr (). round (3)
	       assists rebound points
assists 1.000 -0.245 -0.330
rebounds -0.245 1.000 -0.522
points -0.330 -0.522 1.000

Крок 3: Інтерпретація кореляційної матриці.

Усі коефіцієнти кореляції вздовж діагоналі таблиці дорівнюють 1, оскільки кожна змінна ідеально корелює сама із собою.

Усі інші коефіцієнти кореляції вказують на кореляцію між різними попарними комбінаціями змінних. Наприклад:

• Коефіцієнт кореляції між передачами та підбираннями становить -0,245 .
• Коефіцієнт кореляції між передачами та очками становить -0,330 .
• Коефіцієнт кореляції між підбираннями та очками становить -0,522 .

Крок 4: Візуалізуйте кореляційну матрицю (необов’язково).

Ви можете візуалізувати кореляційну матрицю за допомогою параметрів стилю, доступних у pandas:

 corr = df. corr ()
corr. style . background_gradient (cmap='coolwarm')

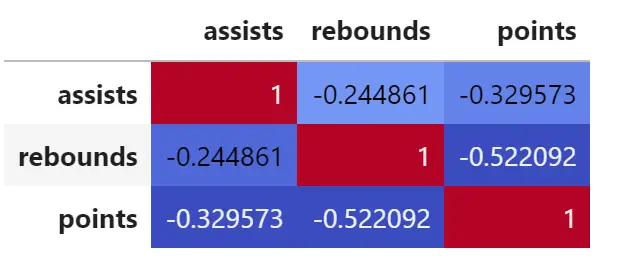
Ви також можете змінити аргумент cmap , щоб створити кореляційну матрицю з різними кольорами.

 corr = df. corr ()
corr. style . background_gradient (cmap=' RdYlGn ') 

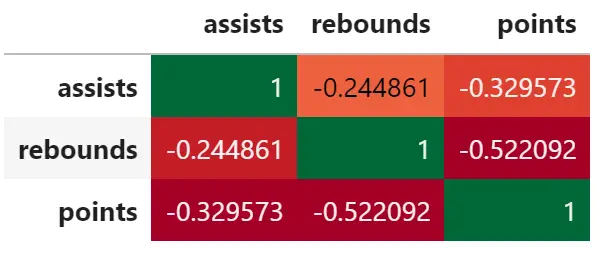
 corr = df. corr ()
corr. style . background_gradient (cmap=' bwr ') 

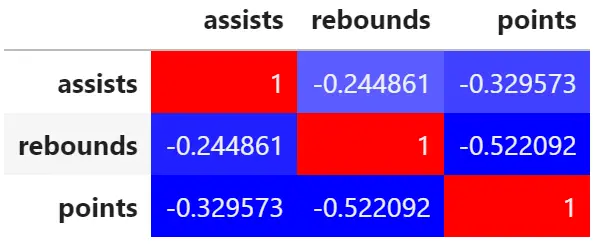
 corr = df. corr ()
corr. style . background_gradient (cmap=' PuOr ') 

Примітка : повний список аргументів cmap див. у документації matplotlib .