Як розрахувати кореляцію між категоріальними змінними

Ми часто використовуємо коефіцієнт кореляції Пірсона для обчислення кореляції між безперервними числовими змінними.

Однак нам потрібно використовувати іншу метрику для обчислення кореляції між категоріальними змінними, тобто змінними, які мають імена або мітки, наприклад:

• Сімейний стан (незаміжня, одружена, розлучена)
• Статус куріння (курить, не курить)
• Колір очей (блакитні, карі, зелені)

Для обчислення кореляції між категоріальними змінними використовують три стандартні показники:

1. Тетрахорична кореляція: використовується для обчислення кореляції між бінарними категоріальними змінними.

2. Поліхорична кореляція: використовується для обчислення кореляції між порядковими категоріальними змінними.

3. V Крамера: використовується для обчислення кореляції між номінальними категоріальними змінними.

У наступних розділах наведено приклад того, як обчислити кожне з цих трьох вимірювань.

Метрика 1: тетрахорична кореляція

Тетрахорична кореляція використовується для обчислення кореляції між бінарними категоріальними змінними. Пам’ятайте, що двійкові змінні – це змінні, які можуть приймати лише одне з двох можливих значень.

Значення тетрахоричної кореляції коливається від -1 до 1, де -1 означає сильну негативну кореляцію, 0 означає відсутність кореляції, а 1 означає сильну позитивну кореляцію.

Наприклад, припустімо, що ми хочемо знати, чи пов’язана стать із перевагами політичної партії. Тож ми беремо просту випадкову вибірку зі 100 виборців і запитуємо їх про їхні переваги щодо політичної партії.

У наступній таблиці представлені результати опитування:

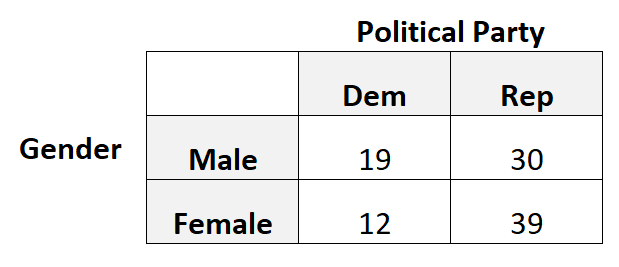
У цьому сценарії ми б використали тетрахоричну кореляцію, оскільки кожна категоріальна змінна є бінарною, тобто кожна змінна може приймати лише два можливі значення.

Ми можемо використати наступний код у R, щоб обчислити тетрахоричну кореляцію між двома змінними:

 library (psych)

#create 2x2 table
data = matrix(c(19, 12, 30, 39), nrow= 2 )

#view table
data

#calculate tetrachoric correlation
tetrachoric(data)

tetrachoric correlation 
[1] 0.27

Тетрахоричне співвідношення виявляється рівним 0,27 . Це значення є досить низьким, що вказує на те, що існує слабкий (якщо такий є) зв’язок між статтю та перевагами політичної партії.

Показник 2: Поліхорична кореляція

Поліхорична кореляція використовується для обчислення кореляції між порядковими категоріальними змінними. Нагадаємо, що порядкові змінні – це змінні, можливі значення яких мають природний порядок.

Значення поліхорічної кореляції коливається від -1 до 1, де -1 означає сильну негативну кореляцію, 0 означає відсутність кореляції, а 1 означає сильну позитивну кореляцію.

Наприклад, скажімо, ви хочете знати, чи два різні агентства рейтингу фільмів мають високу кореляцію між рейтингами своїх фільмів.

Ми просимо кожне агентство оцінити 20 різних фільмів за шкалою від 1 до 3, де 1 означає «погано», 2 — «погано», а 3 — «добре».

У наступній таблиці показано результати:

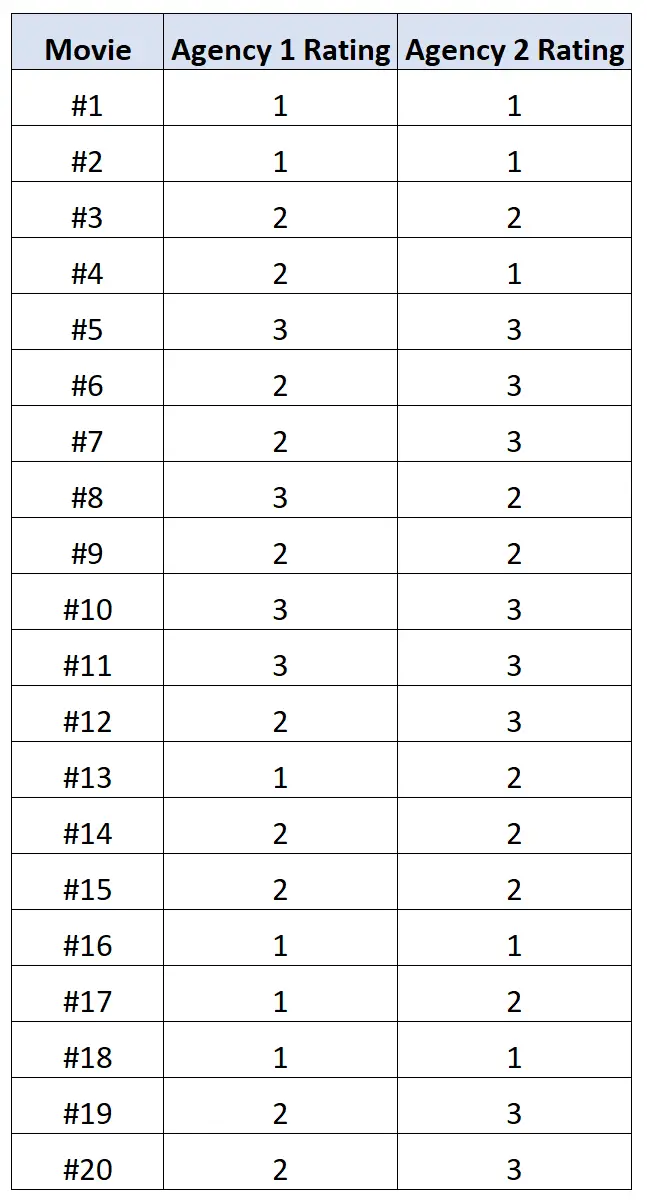
Ми можемо використати такий код у R, щоб обчислити поліхорічну кореляцію між рейтингами двох агентств:

 library (polycor)

#define movie ratings
x <- c(1, 1, 2, 2, 3, 2, 2, 3, 2, 3, 3, 2, 1, 2, 2, 1, 1, 1, 2, 2)
y <- c(1, 1, 2, 1, 3, 3, 3, 2, 2, 3, 3, 3, 2, 2, 2, 1, 2, 1, 3, 3)

#calculate polychoric correlation between ratings
polychor(x, y)

[1] 0.7828328

Поліхорична кореляція виявляється рівною 0,78 . Це значення досить високе, що вказує на те, що існує сильний позитивний зв’язок між рейтингами кожного агентства.

Метрика 3: Крамер V

V Крамера використовується для розрахунку кореляції між номінальними категоріальними змінними. Пам’ятайте, що номінальні змінні – це ті, які містять мітки категорії, але не мають природного порядку.

Значення V Крамера коливається від 0 до 1, де 0 вказує на відсутність зв’язку між змінними, а 1 вказує на сильний зв’язок між змінними.

Наприклад, скажімо, ми хочемо знати, чи існує кореляція між кольором очей і статтю. Тому ми опитуємо 50 осіб і отримуємо такі результати:

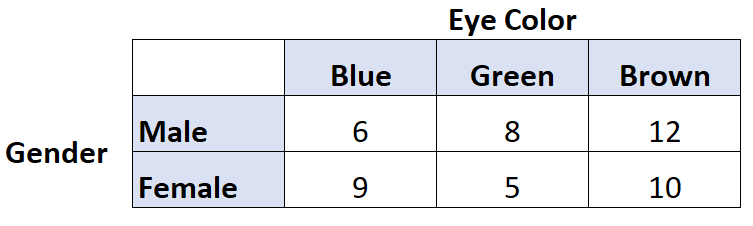
Ми можемо використати такий код у R, щоб обчислити V Крамера для цих двох змінних:

 library (rcompanion)

#create table
data = matrix(c(6, 9, 8, 5, 12, 10), nrow= 2 )

#view table
data

     [,1] [,2] [,3]
[1,] 6 8 12
[2,] 9 5 10

#calculate Cramer's V
cramerV(data)

Cramer V 
  0.1671

V Крамера виявляється 0,1671 . Це значення є досить низьким, що вказує на слабкий зв’язок між статтю та кольором очей.

Додаткові ресурси

Введення в коефіцієнт кореляції Пірсона
Ознайомлення з тетрахоричним співвідношенням
Категориальні чи кількісні змінні: у чому різниця?
Рівні вимірювання: номінальний, порядковий, інтервальний та коефіцієнтний