Що таке криволінійна регресія? (визначення та приклади)
Криволінійна регресія — це назва будь-якої моделі регресії, яка намагається підігнати криву , а не пряму лінію.
Загальні приклади моделей криволінійної регресії включають:
Квадратична регресія: використовується, коли існує квадратичний зв’язок між прогностичною змінною та змінною відповіді . На графіку цей тип зв’язку виглядає як «U» або перевернуте «U» на діаграмі розсіювання:
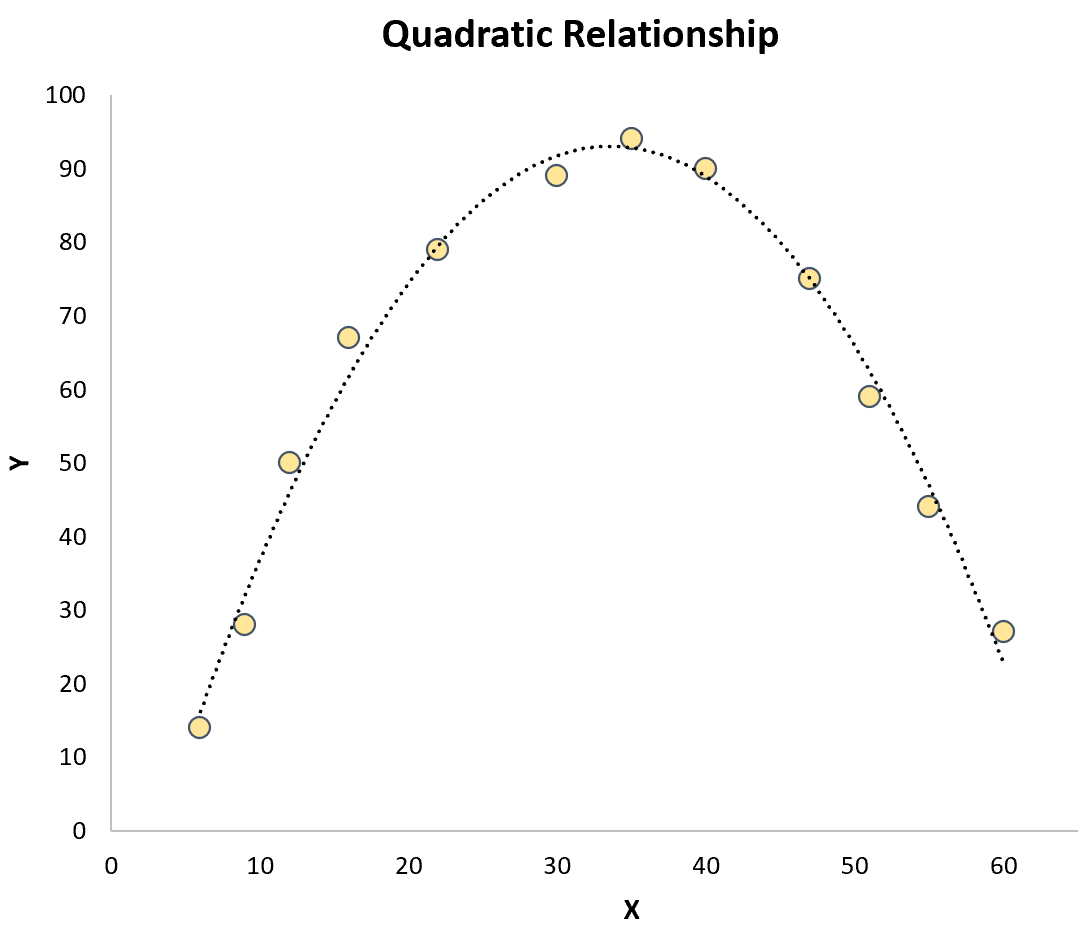
Кубічна регресія: використовується, коли існує кубічний зв’язок між змінною предиктора та змінною відповіді. На графіку цей тип зв’язку показує дві чіткі криві на діаграмі розсіювання:
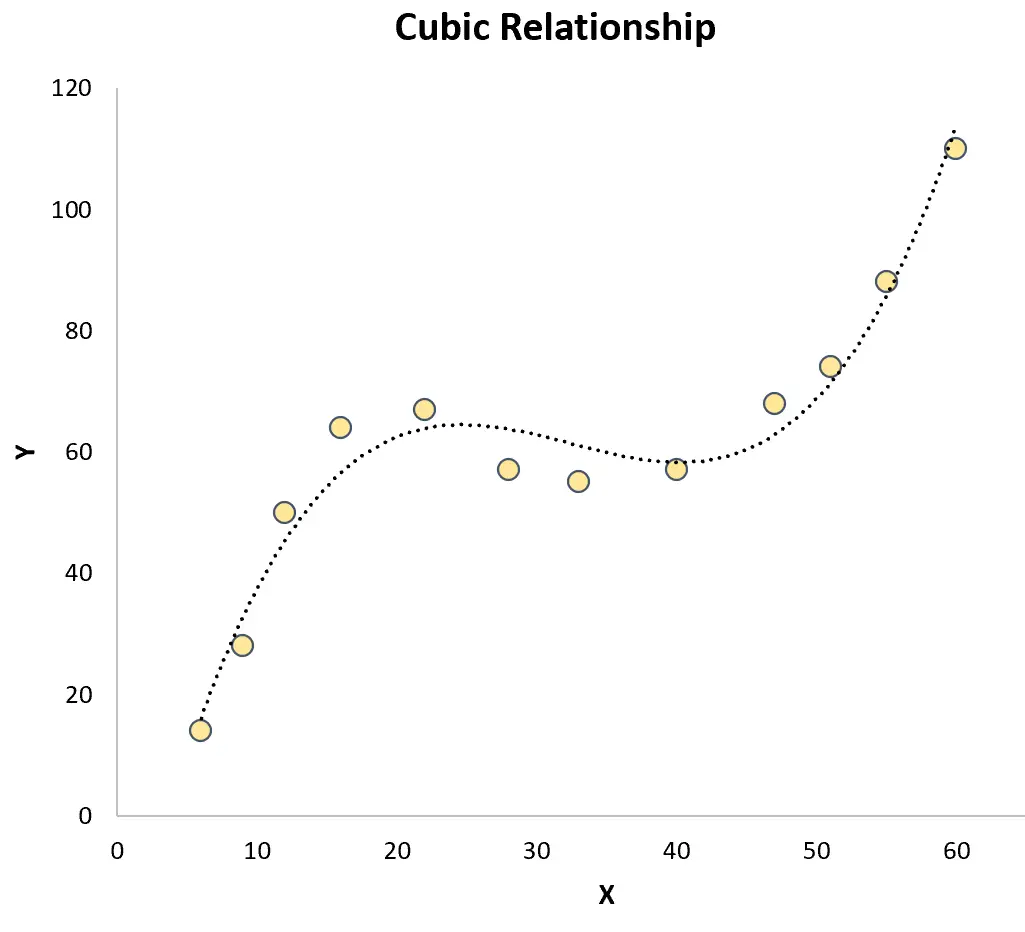
Обидва вони відрізняються від простої лінійної регресії , у якій зв’язок між змінною предиктора та змінною відповіді є лінійним:
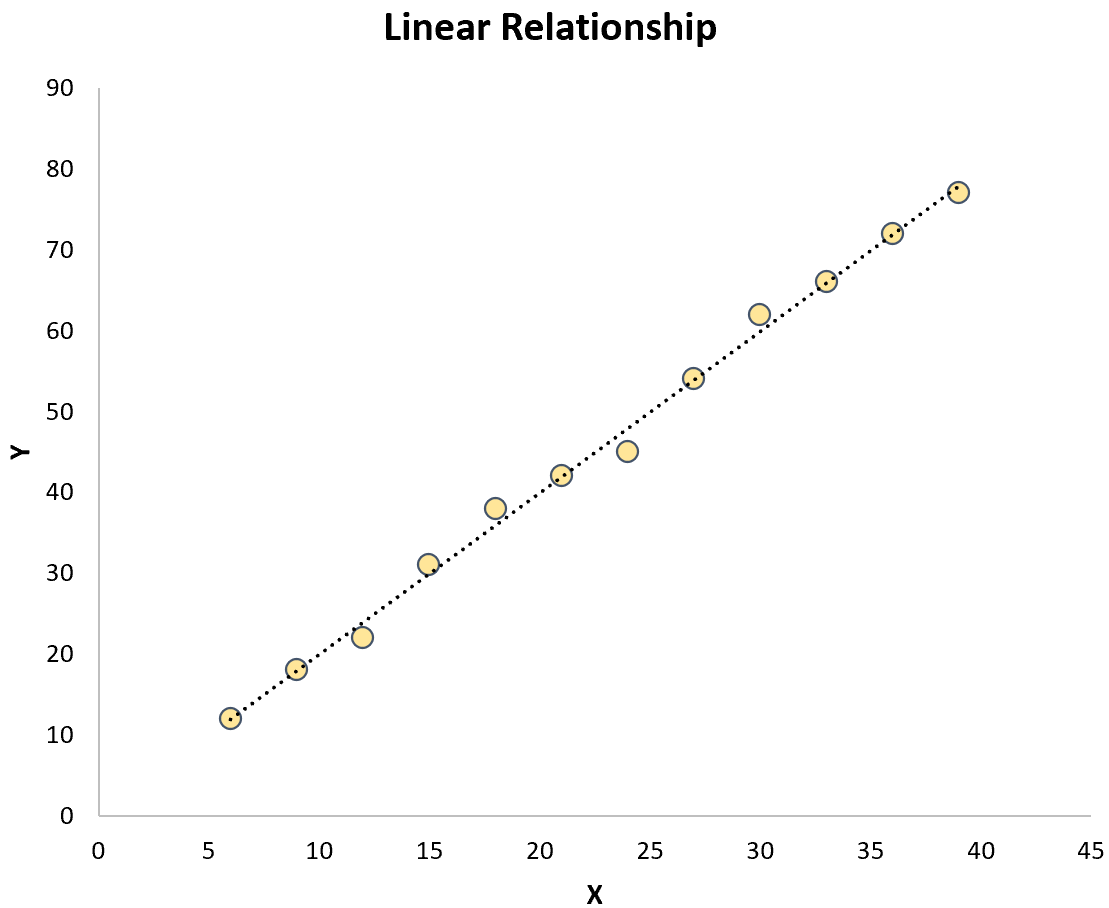
Формула для моделей криволінійної регресії
Проста модель лінійної регресії намагається підібрати набір даних за такою формулою:
ŷ = β 0 + β 1 x
золото:
- ŷ: змінна відповіді
- β 0 , β 1 : Коефіцієнти регресії
- x: передбачувана змінна
На відміну від цього, модель квадратичної регресії використовує таку формулу:
ŷ = β 0 + β 1 x + β 2 x 2
А модель кубічної регресії використовує таку формулу:
ŷ = β 0 + β 1 x + β 2 x 2 + β 3 x 3
Більш загальна назва регресійних моделей, які включають експоненту, — поліноміальна регресія , яка приймає таку формулу:
ŷ = β 0 + β 1 x + β 2 x 2 + … + β k x k
Значення k вказує на ступінь полінома. Хоча ступінь може бути будь-яким позитивним числом, на практиці ми рідко використовуємо поліноміальні регресійні моделі зі ступенем, більшим за 3 або 4.
Використовуючи експоненти у формулі моделі регресії, моделі поліноміальної регресії можуть підганяти криві до наборів даних замість прямих ліній.
Коли використовувати криволінійну регресію
Найпростіший спосіб дізнатися, чи варто вам використовувати криволінійну регресію чи ні, це створити діаграму розсіювання змінної предиктора та змінної відповіді.
Якщо діаграма розсіювання показує лінійну залежність між двома змінними, проста лінійна регресія, ймовірно, буде доречною.
Однак, якщо діаграма розсіювання показує квадратичну, кубічну або іншу криволінійну структуру між предиктором і змінною відповіді, тоді криволінійна регресія, ймовірно, більш доцільна для використання.
Ви також можете підібрати просту модель лінійної регресії та модель криволінійної регресії та порівняти підібрані значення R-квадрат кожної моделі, щоб визначити, яка модель забезпечує найкращу відповідність даним.
Скоригований R-квадрат корисний, оскільки він говорить вам, яку частину дисперсії у змінній відповіді можна пояснити змінною(ями) предиктора, скоригованою на кількість змінних предиктора в моделі.
Загалом, модель із найвищим скоригованим значенням R-квадрат забезпечує кращу відповідність набору даних.
Додаткові ресурси
У наступних посібниках пояснюється, як виконувати поліноміальну регресію в різних статистичних програмах:
Вступ до поліноміальної регресії
Як виконати поліноміальну регресію в Excel
Як виконати поліноміальну регресію в Python
Як виконати поліноміальну регресію в R
Про автора
Редакція
Привіт, я Бенджамін, професор статистики на пенсії, який став викладачем статистики. Маючи великий досвід і знання в галузі статистики, я готовий поділитися своїми знаннями, щоб розширити можливості студентів через Statorials. Дізнайтеся більше