Як виконати кубічну регресію в python

Кубічна регресія — це тип регресії, який ми можемо використовувати для кількісного визначення зв’язку між змінною-прогнозом і змінною відповіді, коли зв’язок між змінними є нелінійним.

Цей підручник пояснює, як виконати кубічну регресію в Python.

Приклад: кубічна регресія в Python

Припустімо, що ми маємо наступний DataFrame pandas, який містить дві змінні (x і y):

 import pandas as pd

#createDataFrame
df = pd. DataFrame ({' x ': [6, 9, 12, 16, 22, 28, 33, 40, 47, 51, 55, 60],
                   ' y ': [14, 28, 50, 64, 67, 57, 55, 57, 68, 74, 88, 110]})

#view DataFrame
print (df)

     xy
0 6 14
1 9 28
2 12 50
3 16 64
4 22 67
5 28 57
6 33 55
7 40 57
8 47 68
9 51 74
10 55 88
11 60 110

Якщо ми зробимо просту діаграму розсіювання цих даних, то побачимо, що зв’язок між двома змінними є нелінійним:

 import matplotlib. pyplot as plt

#create scatterplot
plt. scatter (df. x , df. y ) 

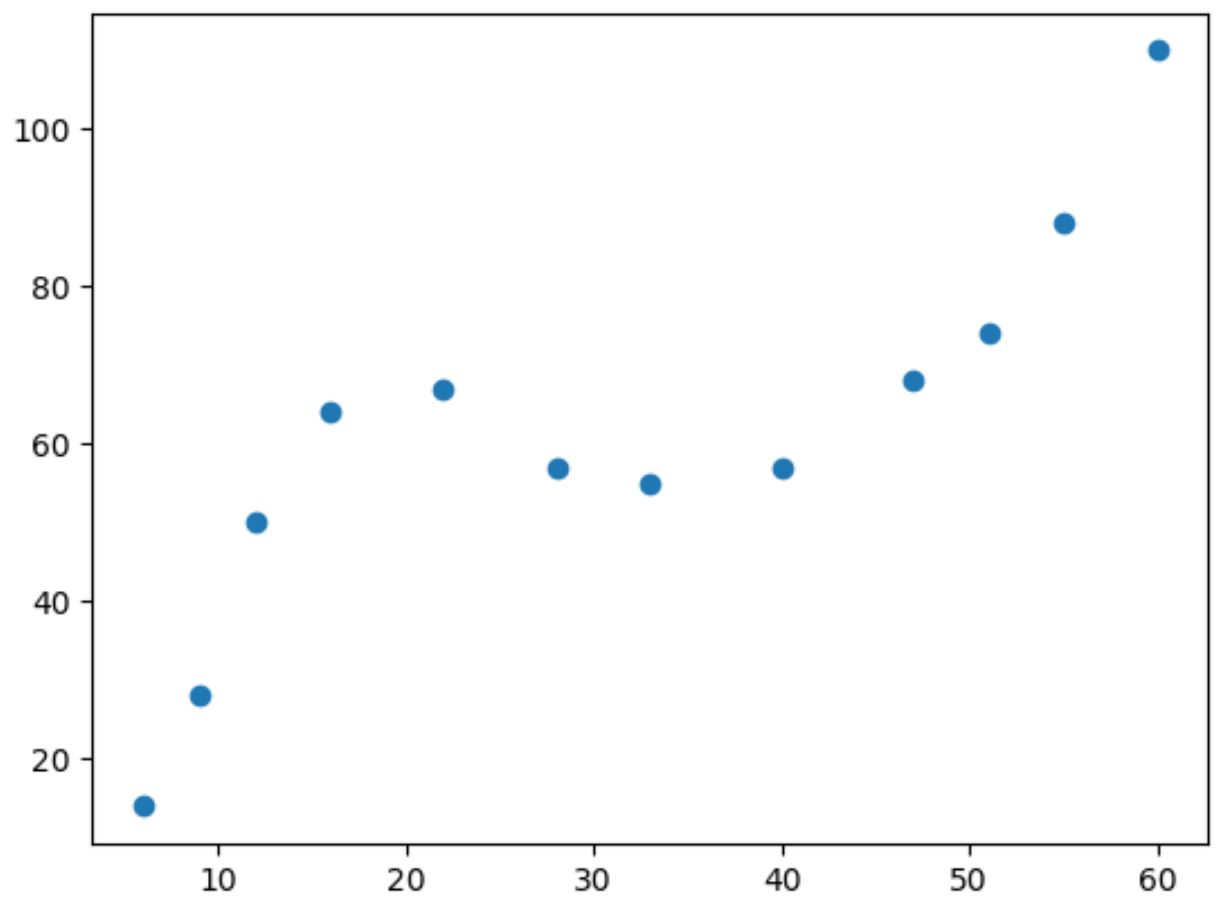
У міру збільшення значення x y зростає до певної точки, потім зменшується, а потім знову збільшується.

Цей візерунок із двома «кривими» на графіку є показником кубічної залежності між двома змінними.

Це означає, що модель кубічної регресії є хорошим кандидатом для кількісного визначення зв’язку між двома змінними.

Щоб виконати кубічну регресію, ми можемо підібрати модель поліноміальної регресії зі ступенем 3 за допомогою функції numpy.polyfit() :

 import numpy as np

#fit cubic regression model
model = np. poly1d (np. polyfit (df. x , df. y , 3))

#add fitted cubic regression line to scatterplot
polyline = np. linspace (1, 60, 50)
plt. scatter (df. x , df. y )
plt. plot (polyline, model(polyline))

#add axis labels
plt. xlabel (' x ')
plt. ylabel (' y ')

#displayplot
plt. show () 

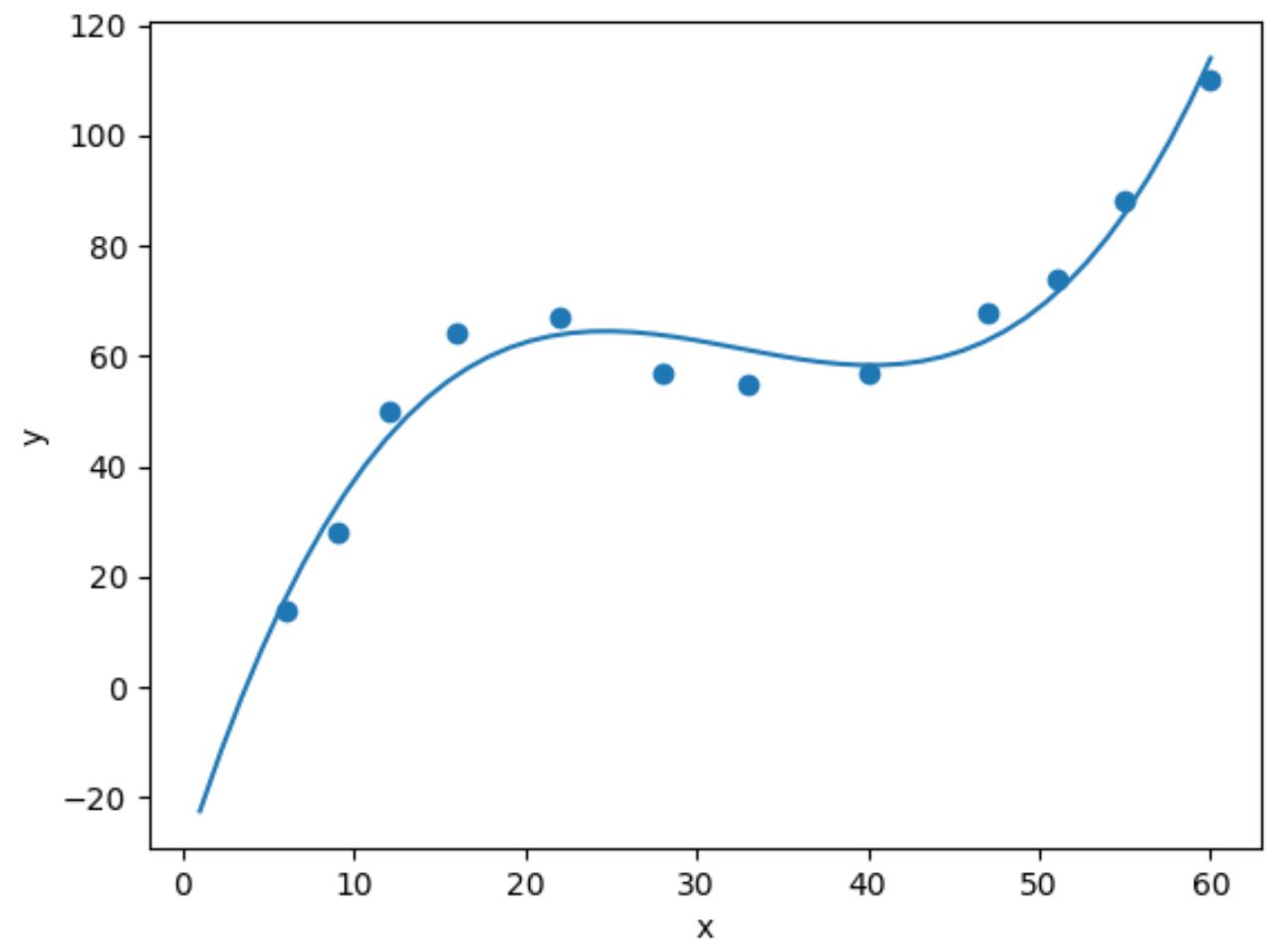
Ми можемо отримати підігнане рівняння кубічної регресії, надрукувавши коефіцієнти моделі:

 print (model)

          3 2
0.003302x - 0.3214x + 9.832x - 32.01

Зібране рівняння кубічної регресії має вигляд:

y = 0,003302(x) ³ – 0,3214(x) ² + 9,832x – 30,01

Ми можемо використовувати це рівняння, щоб обчислити очікуване значення y на основі значення x.

Наприклад, якщо x дорівнює 30, то очікуване значення для y дорівнює 64,844:

y = 0,003302(30) ³ – 0,3214(30) ² + 9,832(30) – 30,01 = 64,844

Ми також можемо написати коротку функцію, щоб отримати R-квадрат моделі, який є часткою дисперсії у змінній відповіді, яку можна пояснити змінними предиктора.

 #define function to calculate r-squared
def polyfit(x, y, degree):
    results = {}
    coeffs = np. polyfit (x, y, degree)
    p = np. poly1d (coeffs)
    #calculate r-squared
    yhat = p(x)
    ybar = np. sum (y)/len(y)
    ssreg = np. sum ((yhat-ybar) ** 2)
    sstot = np. sum ((y - ybar) ** 2)
    results[' r_squared '] = ssreg / sstot

    return results

#find r-squared of polynomial model with degree = 3
polyfit(df. x , df. y , 3)

{'r_squared': 0.9632469890057967}

У цьому прикладі R-квадрат моделі становить 0,9632 .

Це означає, що 96,32% варіації змінної відповіді можна пояснити змінною предиктора.

Оскільки це значення дуже високе, це говорить нам про те, що модель кубічної регресії добре кількісно визначає зв’язок між двома змінними.

За темою: що таке хороше значення R-квадрат?

Додаткові ресурси

У наступних посібниках пояснюється, як виконувати інші типові завдання в Python:

Як виконати просту лінійну регресію в Python
Як виконати квадратичну регресію в Python
Як виконати поліноміальну регресію в Python