Логістична регресія

за Редакція 2 Серпня, 2023 Статистика 0 коментарів

У цій статті пояснюється, що таке логістична регресія в статистиці. Так само ви знайдете формулу логістичної регресії, різні типи логістичної регресії та, крім того, розв’язану вправу логістичної регресії.

Що таке логістична регресія?

У статистиці логістична регресія — це тип регресійної моделі, яка використовується для прогнозування результату категоріальної змінної . Тобто логістична регресія використовується для моделювання ймовірності того, що категоріальна змінна набуває певного значення на основі незалежних змінних.

Найбільш поширеною моделлю логістичної регресії є бінарна логістична регресія, у якій є лише два можливі результати: «невдача» або «успіх» ( розподіл Бернуллі ). «Невдача» представлена значенням 0, тоді як «успіх» представлено значенням 1.

Наприклад, ймовірність того, що студент складе іспит на основі годин, які він витратив на навчання, можна вивчити за допомогою моделі логістичної регресії. У цьому випадку невдача була б результатом «провалу», а, з іншого боку, успіх був би результатом «успіху».

Формула логістичної регресії

Рівняння для моделі логістичної регресії таке:

$\displaystyle \ln \left(\frac{p}{1-p}\right) =\beta_0+\beta_1x_1+\beta_2x_2+\dots+\beta_ix_i$

Тому в моделі логістичної регресії ймовірність отримання результату «успіх», тобто того, що залежна змінна приймає значення 1, розраховується за такою формулою:

$p=\cfrac{1}{1+e^{-(\beta_0+\beta_1x_1+\beta_2x_2+\dots+\beta_ix_i)}}$

золото:

$p$

це ймовірність того, що залежна змінна дорівнює 1.
$\beta_0$

є константою моделі логістичної регресії.
$\beta_i$

– коефіцієнт регресії змінної i.
$x_i$

є значенням змінної i.

Приклад моделі логістичної регресії

Тепер, коли ми знаємо визначення логістичної регресії, давайте розглянемо конкретний приклад того, як створити модель цього типу регресії.

У наведеній нижче таблиці зібрано серію з 20 фрагментів даних, які пов’язують навчальні години кожного студента та те, склали чи не склали вони статистичний іспит. Запустіть модель логістичної регресії та обчисліть ймовірність того, що студент пройде, якщо він чи вона провчиться 4 години.

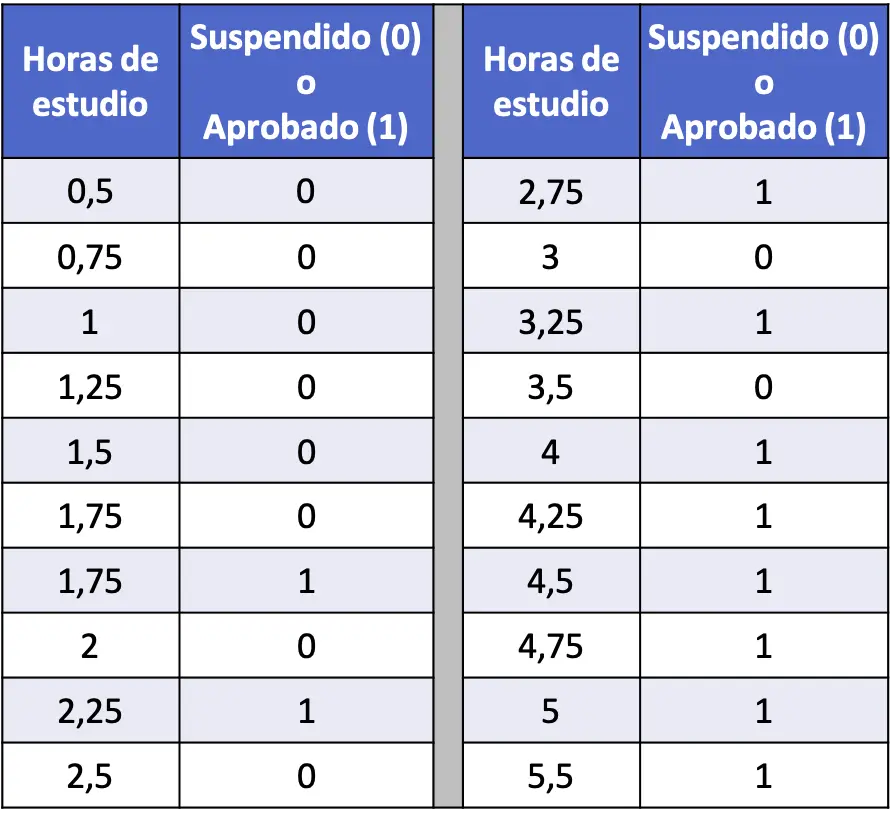
У цьому випадку пояснювальною змінною є кількість годин навчання, а змінною відповіді є те, чи студент зазнав невдачі (0) чи склав (1). Тому в нашій моделі ми матимемо лише коефіцієнт

$\beta_0$

і коефіцієнт

$\beta_1$

, оскільки є лише одна незалежна змінна.

$\beta_0 \qquad \beta_1$

Визначення коефіцієнтів регресії вручну є дуже трудомістким, тому рекомендується використовувати комп’ютерну програму типу Minitab. Таким чином, значення коефіцієнтів регресії, розраховані за допомогою Minitab, наступні:

$\begin{array}{c}\beta_0\approx -4,1\\[2ex]\beta_1\approx 1,5\end{array}$

Таким чином, модель логістичної регресії виглядає так:

$\begin{aligned}p&=\cfrac{1}{1+e^{-(\beta_0+\beta_1x_1+\beta_2x_2+\dots+\beta_ix_i)}}\\[2ex]p&=\cfrac{1}{1+e^{-(-4,1+1,5x_1)}}\\[2ex]p&=\cfrac{1}{1+e^{4,1-1,5x_1}}\end{aligned}$

Нижче ви можете побачити зразки даних і рівняння моделі логістичної регресії в графіку:

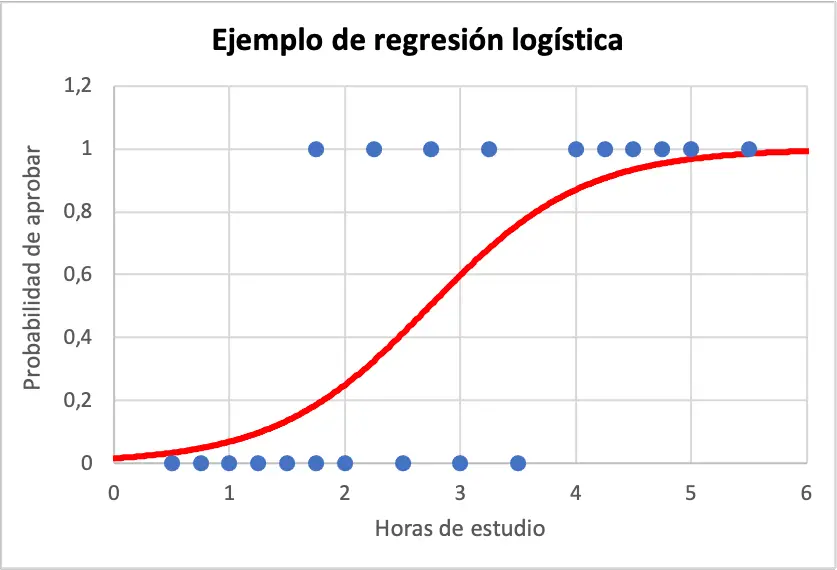
Таким чином, щоб обчислити ймовірність того, що студент досягне успіху, якщо він або вона навчався 4 години, просто використовуйте рівняння, отримане з моделі логістичної регресії:

$\begin{aligned}p&=\cfrac{1}{1+e^{4,1-1,5x_1}}\\[2ex]p&=\cfrac{1}{1+e^{4,1-1,5\cdot 4}}\\[2ex]p&=0,8699\end{aligned}$

Коротше кажучи, якщо студент навчається чотири години, він матиме 86,99% ймовірності скласти іспит.

Типи логістичної регресії

Існує три види логістичної регресії :

Двійкова логістична регресія : залежна змінна може мати лише два значення (0 і 1).
Мультиноміальна логістична регресія : залежна змінна має більше двох можливих значень.
Порядкова логістична регресія : можливі результати мають природний порядок.

Логістична регресія та лінійна регресія

Нарешті, підводячи підсумок, ми побачимо, яка різниця між логістичною регресією та лінійною регресією, оскільки найбільш використовуваною регресійною моделлю в статистиці є лінійна модель.

Лінійна регресія використовується для моделювання числових залежних змінних. Крім того, у лінійній регресії зв’язок між пояснювальними змінними та змінною відповіді є лінійним.

Тому основною відмінністю між логістичною регресією та лінійною регресією є тип залежної змінної. У логістичній регресії залежна змінна є категоричною, тоді як залежна змінна в лінійній регресії є чисельною.

Таким чином, логістична регресія використовується для прогнозування результату між двома можливими варіантами, тоді як лінійна регресія допомагає передбачити числовий результат.

Про автора

Редакція

Привіт, я Бенджамін, професор статистики на пенсії, який став викладачем статистики. Маючи великий досвід і знання в галузі статистики, я готовий поділитися своїми знаннями, щоб розширити можливості студентів через Statorials. Дізнайтеся більше