Excel: як використовувати linest для виконання множинної лінійної регресії
Ви можете використовувати функцію ЛІНІЙНИЙ в Excel, щоб адаптувати модель множинної лінійної регресії до набору даних.
Ця функція використовує такий базовий синтаксис:
= LINEST ( known_y's, [known_x's], [const], [stats] )
золото:
- відомі_y : масив відомих значень y
- відомі_x : масив відомих значень x
- const : необов’язковий аргумент. Якщо TRUE, константа b обробляється нормально. Якщо значення FALSE, константа b має значення 1.
- stats : необов’язковий аргумент. Якщо TRUE, повертається додаткова статистика регресії. Якщо FALSE, додаткова регресійна статистика не повертається.
Наступний покроковий приклад показує, як використовувати цю функцію на практиці.
Крок 1: Введіть дані
Спочатку давайте введемо такий набір даних в Excel:
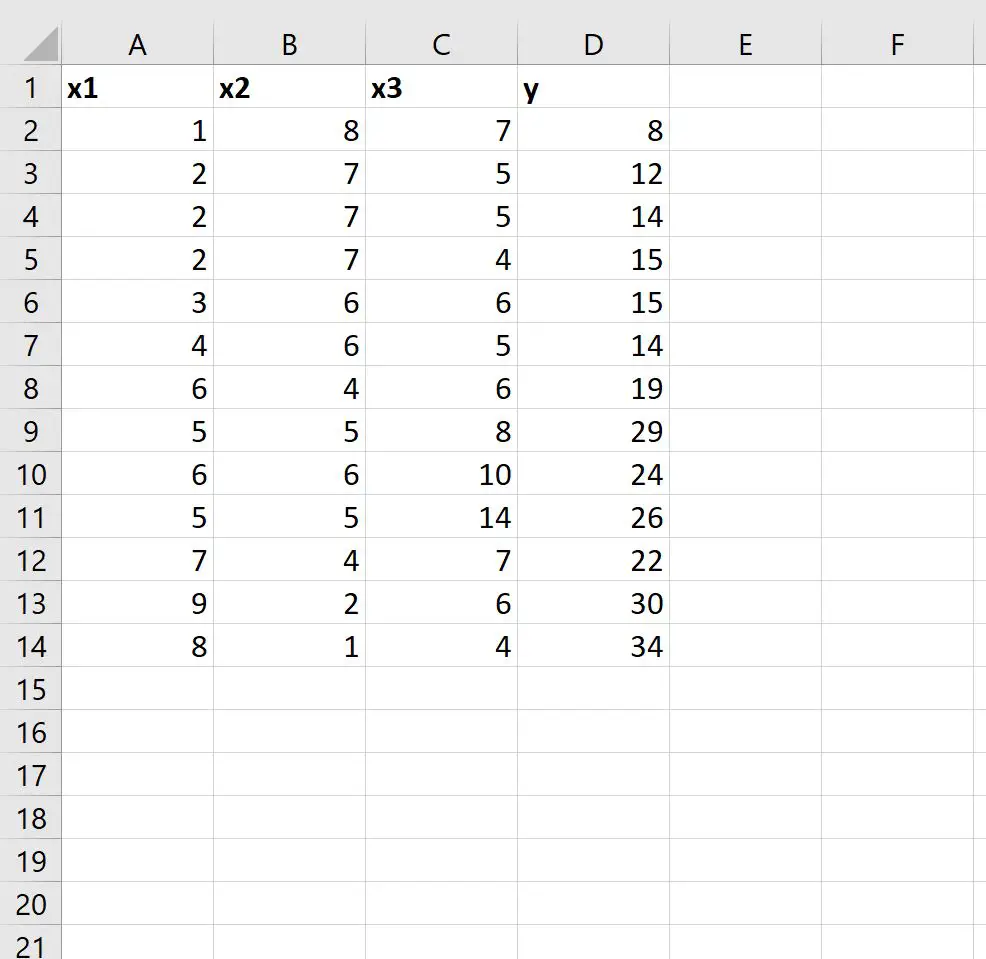
Крок 2. Використовуйте LINEST, щоб підібрати модель множинної лінійної регресії
Припустімо, що ми хочемо підібрати модель множинної лінійної регресії, використовуючи x1 , x2 і x3 як змінні-прогнози та y як змінну відповіді.
Для цього ми можемо ввести таку формулу в будь-яку клітинку, щоб відповідати цій моделі множинної лінійної регресії
=LINEST( D2:D14 , A2:C14 )
На наступному знімку екрана показано, як використовувати цю формулу на практиці:
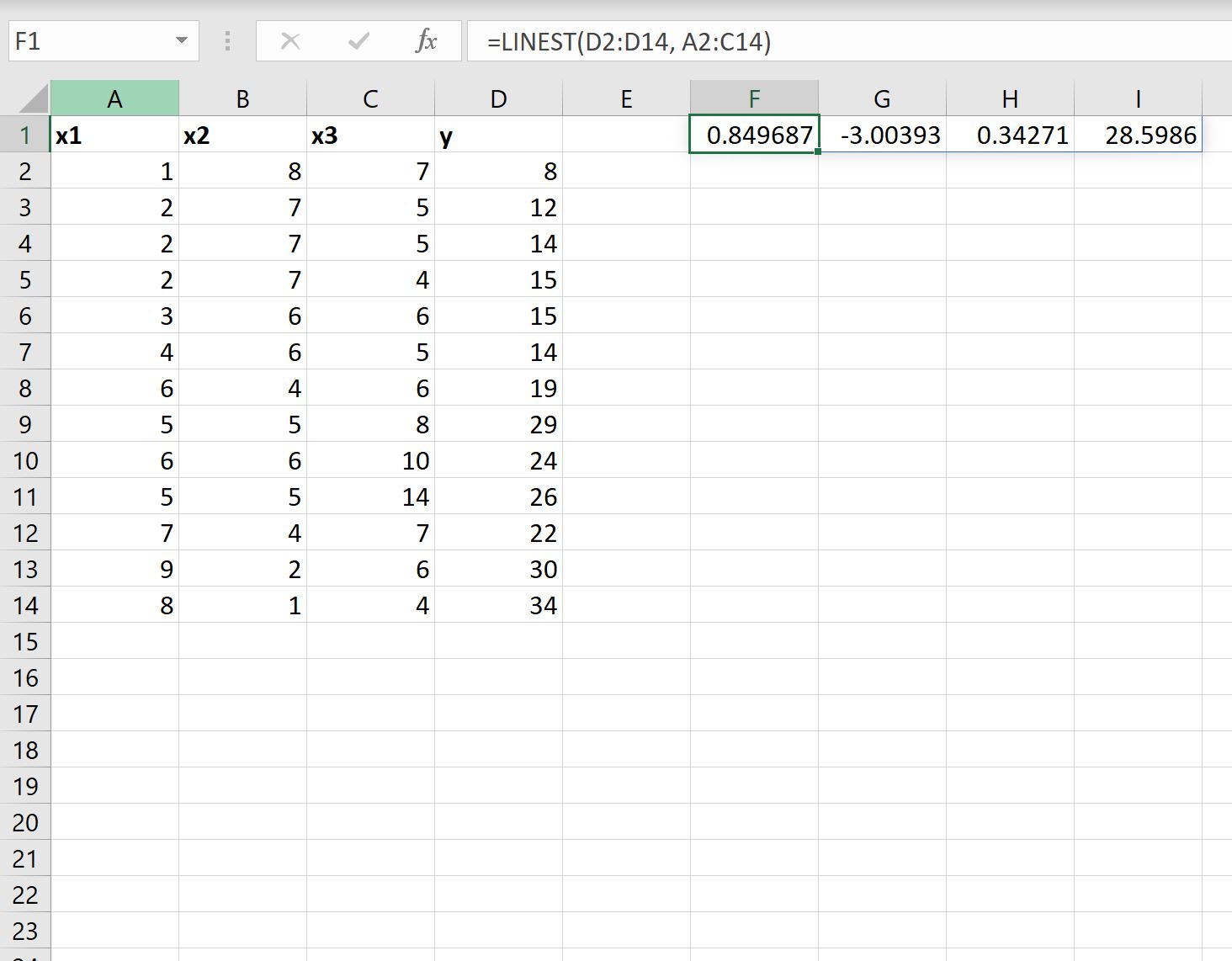
Ось як інтерпретувати результат:
- Коефіцієнт перетину дорівнює 28,5986 .
- Коефіцієнт для x1 становить 0,34271 .
- Коефіцієнт для x2 становить -3,00393 .
- Коефіцієнт для x3 становить 0,849687 .
Використовуючи ці коефіцієнти, ми можемо записати підігнане рівняння регресії наступним чином:
y = 28,5986 + 0,34271(x1) – 3,00393(x2) + 0,849687(x3)
Крок 3 (необов’язково): перегляд додаткової статистики регресії
Ми також можемо встановити значення аргументу stats у функції LINEST рівним TRUE , щоб відобразити додаткову регресійну статистику для підігнаного рівняння регресії:
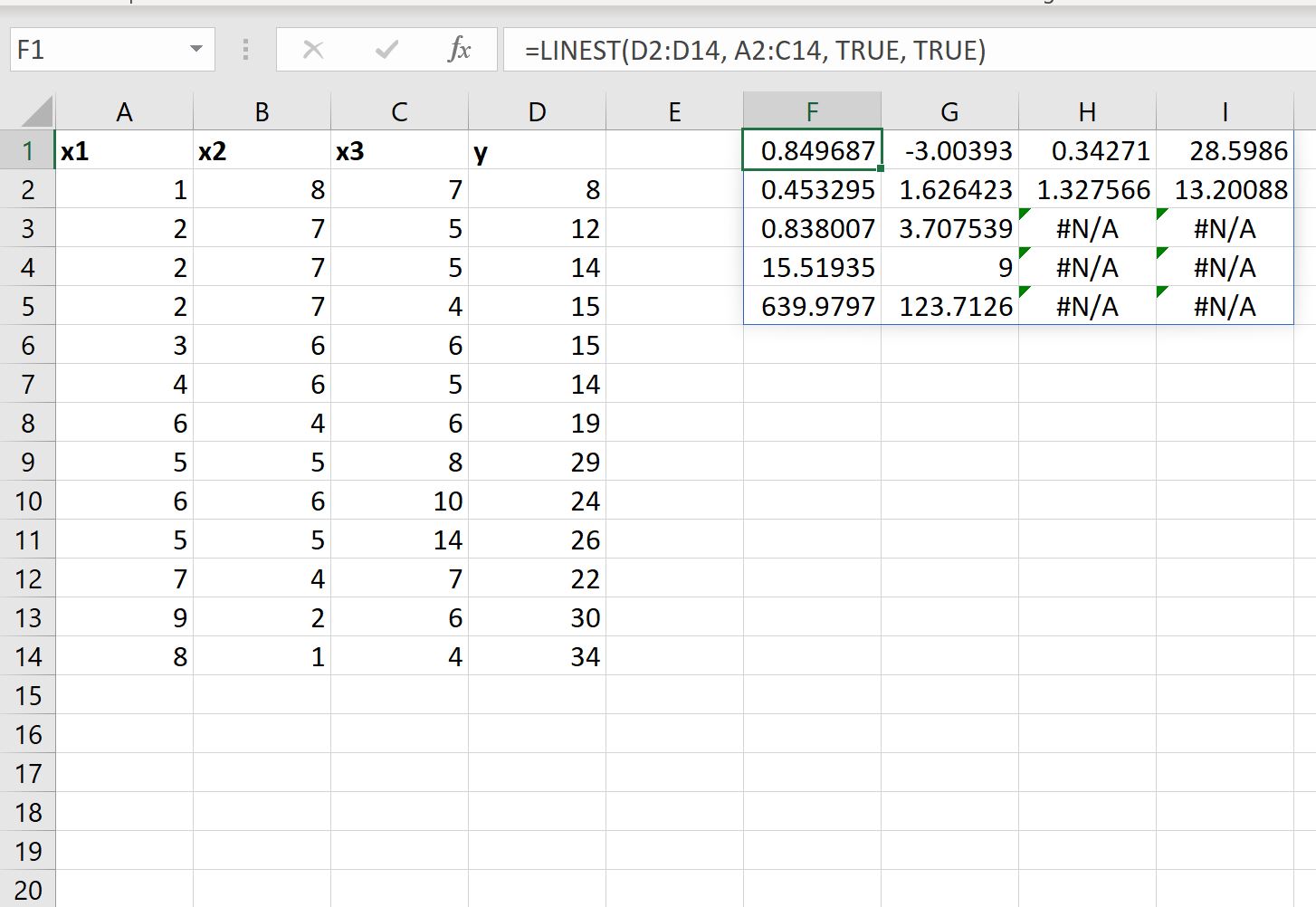
Зібране рівняння регресії залишається незмінним:
y = 28,5986 + 0,34271(x1) – 3,00393(x2) + 0,849687(x3)
Ось як інтерпретувати інші значення результату:
- Стандартна помилка для x3 становить 0,453295 .
- Стандартна помилка для x2 становить 1,626423 .
- Стандартна помилка для x1 становить 1,327566 .
- Стандартна помилка для перехоплення становить 13,20088 .
- R 2 моделі становить .838007 .
- Залишкова стандартна помилка для y становить 3,707539 .
- Загальна статистика F становить 15,51925 .
- Ступенів свободи дорівнює 9 .
- Сума квадратів регресії дорівнює 639,9797 .
- Залишкова сума квадратів дорівнює 123,7126 .
Загалом, мірою, що представляє найбільший інтерес у цій додатковій статистиці, є значення R 2 , яке представляє частку дисперсії у змінній відповіді, яку можна пояснити змінною предиктора.
Значення R 2 може змінюватися від 0 до 1.
Оскільки R 2 цієї конкретної моделі дорівнює 0,838 , це говорить нам про те, що змінні предикторів добре справляються з прогнозуванням значення змінної відповіді y.
За темою: що таке хороше значення R-квадрат?
Додаткові ресурси
У наступних посібниках пояснюється, як виконувати інші типові операції в Excel:
Як використовувати функцію LOGEST в Excel
Як виконати нелінійну регресію в Excel
Як виконати кубічну регресію в Excel