Вступ до мультиноміального розподілу

Мультиноміальний розподіл описує ймовірність отримання певної кількості підрахунків для k різних результатів, коли кожен результат має фіксовану ймовірність появи.

_Якщо випадкову _{величину _} можна знайти за такою формулою :

Імовірність = n! * (p ₁ ^{x ₁} * p ₂ ^{x ₂} * … * p _k ^{x _k} ) / (x ₁ ! * x ₂ ! … * x _k !)

золото:

• n: загальна кількість подій
• x ₁ : кількість разів, коли результат 1 зустрічається
• p ₁ : ймовірність того, що результат 1 відбудеться в даному дослідженні

Наприклад, припустимо, що в урні є 5 червоних кульок, 3 зелених кульки та 2 синіх кульки. Якщо ми навмання витягнемо з урни 5 кульок із заміною, яка ймовірність отримати рівно 2 червоні кульки, 2 зелені кульки та 1 синю кульку?

Щоб відповісти на це запитання, ми можемо використати мультиноміальний розподіл із такими параметрами:

• n : 5
• x ₁ (# червоних кульок) = 2, x ₂ (# зелених кульок) = 2, x ₃ (# синіх кульок) = 1
• p ₁ (червона ймовірність) = 0,5, p ₂ (зелена ймовірність) = 0,3, p ₃ (синя ймовірність) = 0,2

Підставляючи ці числа у формулу, ми знаходимо, що ймовірність:

Імовірність = 5! * (0,5 ² * 0,3 ² * 0,2 ¹ ) / (2! * 2! * 1!) = 0,135 .

Практичні задачі мультиноміального розподілу

Використовуйте наведені нижче практичні завдання, щоб перевірити свої знання про мультиноміальний розподіл.

Примітка. Щоб обчислити відповіді на ці запитання, ми використаємо калькулятор мультиноміального розподілу .

Проблема 1

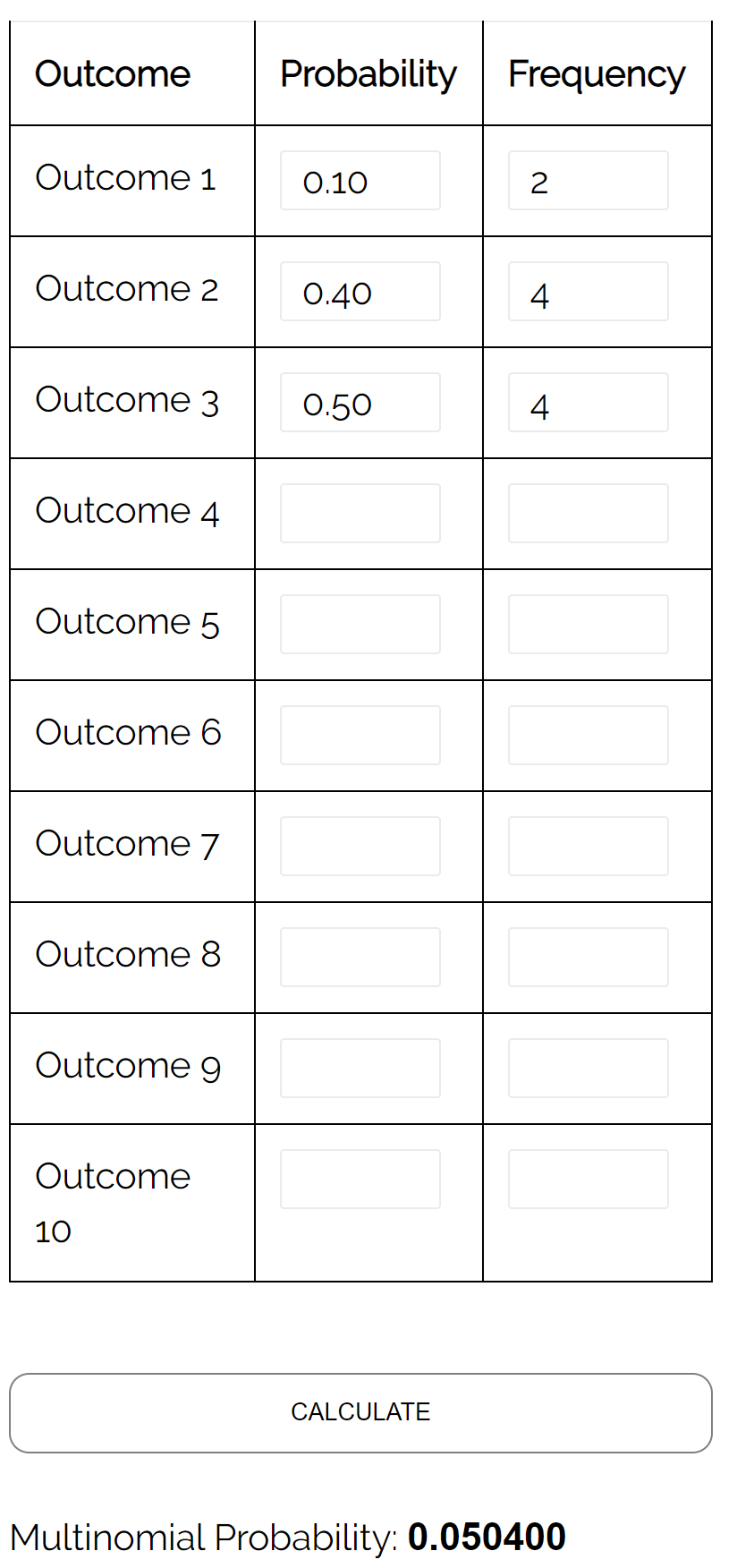
Запитання: На тристоронніх виборах мера кандидат А отримує 10% голосів, кандидат Б отримує 40% голосів, а кандидат С отримує 50% голосів. Якщо ми оберемо випадкову вибірку з 10 виборців, яка ймовірність того, що 2 проголосували за кандидата A, 4 проголосували за кандидата B і 4 проголосували за кандидата C?

Відповідь: Використовуючи калькулятор мультиноміального розподілу з такими вхідними даними, ми знаходимо, що ймовірність дорівнює 0,0504:

Проблема 2

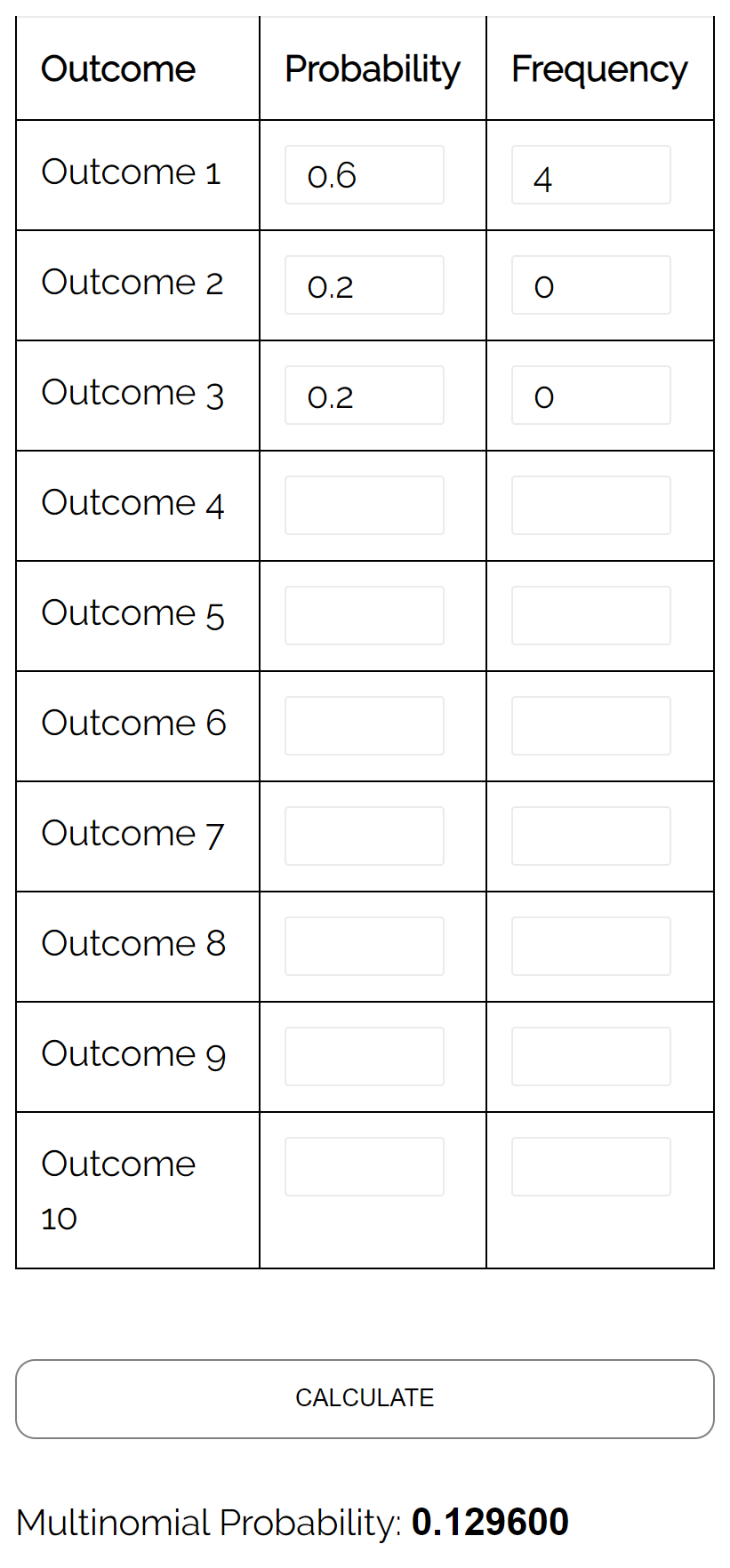
Запитання: Припустимо, що урна містить 6 жовтих кульок, 2 червоних кульки та 2 рожевих кульки. Якщо ми навмання виберемо 4 кулі з урни, замінивши їх, яка ймовірність того, що всі 4 кулі будуть жовтими?

Відповідь: використовуючи калькулятор мультиноміального розподілу з такими вхідними даними, ми знаходимо, що ймовірність становить 0,1296:

Проблема 3

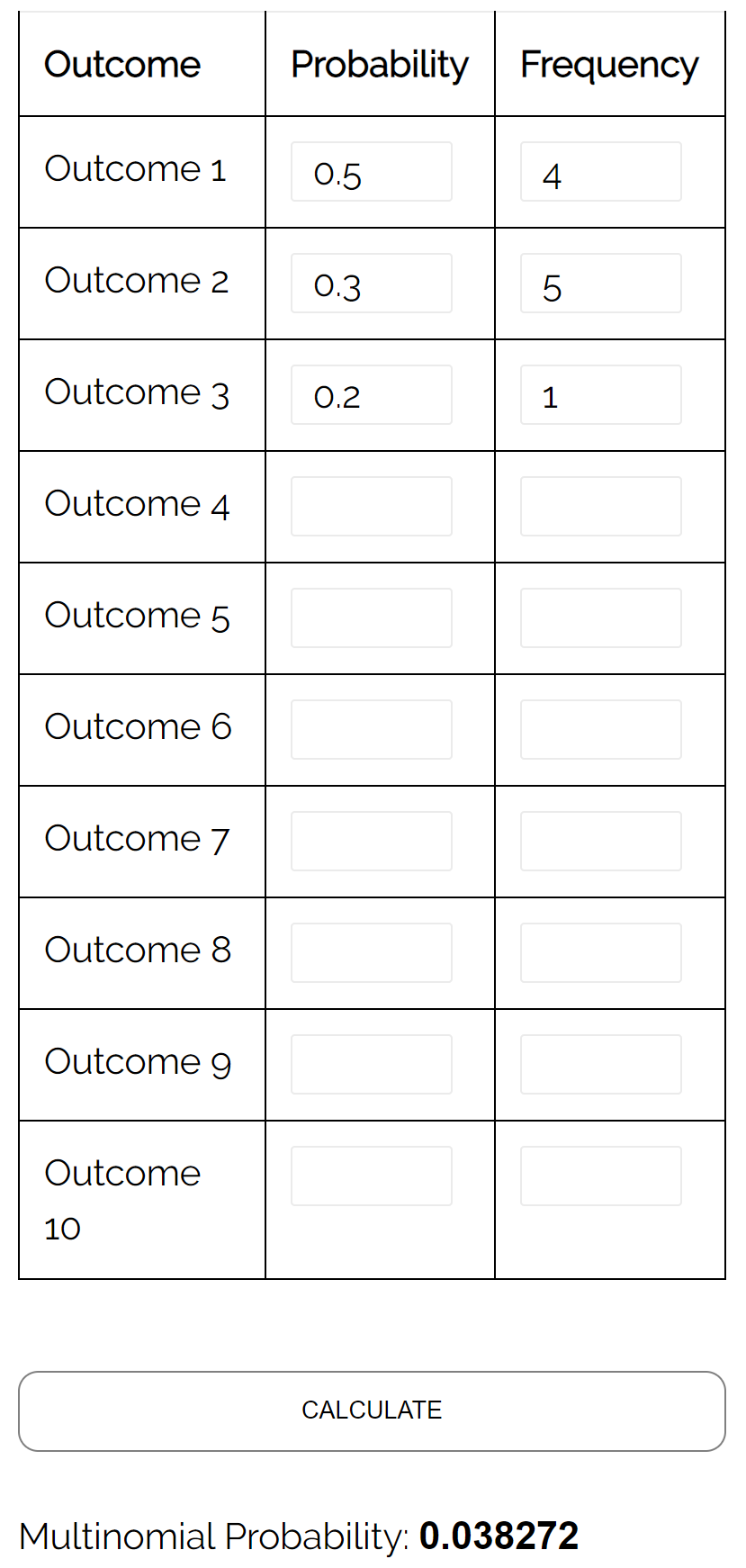
Запитання: Припустимо, що двоє студентів грають у шахи один проти одного. Імовірність того, що учень А виграє певну гру, дорівнює 0,5, ймовірність того, що студент Б виграє певну гру, дорівнює 0,3, а ймовірність того, що в даній грі буде нічия, дорівнює 0, 2. Якщо вони зіграють 10 ігор, яка ймовірність того, що гравець A виграє 4 рази, гравець B виграє 5 разів і що вони 1 раз внічию?

Відповідь: Використовуючи калькулятор мультиноміального розподілу з такими вхідними даними, ми знаходимо, що ймовірність дорівнює 0,038272:

Додаткові ресурси

Наступні навчальні посібники містять вступ до інших поширених розподілів у статистиці:

Введення в нормальний розподіл
Введення в біноміальний розподіл
Введення в розподіл Пуассона
Введення в геометричний розподіл