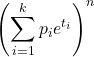Мультиноміальний розподіл

за Редакція 4 Серпня, 2023 Ймовірність 0 коментарів

У цій статті пояснюється, що таке мультиноміальний розподіл у статистиці. Отже, ви знайдете визначення мультиноміального розподілу, його формулу, розв’язану вправу та властивості цього типу розподілу ймовірностей. Крім того, ви зможете розрахувати ймовірність мультиноміального розподілу за допомогою онлайн-калькулятора.

Що таке мультиноміальний розподіл?

Мультиноміальний розподіл (або мультиноміальний розподіл ) — це розподіл ймовірностей, який описує ймовірність кількох взаємовиключних подій, що відбуваються певну кількість разів після кількох випробувань.

Тобто, якщо випадковий експеримент може призвести до трьох або більше ексклюзивних подій і відома ймовірність кожної події окремо, мультиноміальний розподіл використовується для обчислення ймовірності того, що при проведенні кількох експериментів відбудеться певна кількість подій. час кожного разу.

Тому мультиноміальний розподіл є узагальненням біноміального розподілу.

Мультиноміальна формула розподілу

Щоб обчислити ймовірність мультиноміального розподілу, ви повинні спочатку визначити частку між факторіалом загальної кількості даних і факторіалом кількості випадків кожної події, а результат помножити на добуток імовірності кожної події. доведено до кількості випадків зазначеної події.

Іншими словами, формула мультиноміального розподілу має такий вигляд:

золото:

$P$

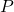
– ймовірність розрахованого мультиноміального розподілу.
$n$

це загальна кількість проведених тестів.
$x_i$

це кількість разів, коли відбувається подія

$i$

.
$p_i$

це ймовірність події

$i$

.

👉 Ви можете скористатися наведеним нижче калькулятором, щоб обчислити ймовірність змінної, яка відповідає поліноміальному розподілу.

Приклад мультиноміального розподілу

Щоб завершити розуміння концепції мультиноміального розподілу, нижче ви розв’язали приклад обчислення ймовірності мультиноміального розподілу.

Магазин продає три різні товари. Коли клієнт робить покупку, ймовірність того, що це буде продукт A, продукт B або продукт C, становить 30%, 15% і 55% відповідно. Знайти ймовірність того, що, коли магазин продав 8 одиниць, 2 належать до товару А, 1 до товару В і 5 до товару С.

Визначена задача регулюється мультиноміальним розподілом, тому необхідно застосувати формулу для цього типу розподілу ймовірностей:

$P=\cfrac{n!}{x_1!\cdot x_2!\cdot x_3!}\cdot p_1^{x_1}\cdot p_2^{x_2}\cdot p_3^{x_3}$

Тому підставляємо дані із задачі у формулу і виконуємо обчислення ймовірності:

$P=\cfrac{8!}{2!\cdot 1!\cdot 5!}\cdot 0,30^{2}\cdot 0,15^{1}\cdot 0,55^{5}=0,114$

Таким чином, ймовірність того, що те, що сказано в постановці проблеми, станеться, становить 11,4%.

Калькулятор мультиноміального розподілу

Запишіть кількість випадків появи кожної події в першому полі та в тому ж порядку ймовірність появи кожної події в другому полі. Потім в останнє порожнє поле введіть загальну кількість зроблених спроб.

Дані повинні бути розділені пробілом і введені крапкою як десятковим роздільником.

Властивості багаточленного розподілу

Мультиноміальний розподіл має такі характеристики:

У мультиноміальному розподілі очікуване значення кількості разів, коли подія i відбувається під час виконання n випробувань, дорівнює загальній кількості виконаних випробувань, помноженій на ймовірність події.

$E[x_i]=n\cdot p_i$

У мультиноміальному розподілі дисперсія для події i обчислюється за таким виразом:

$Var(x_i)=n\cdot p_i\cdot (1-p_i)$

Так само коваріація між двома подіями еквівалентна добутку загальної кількості випробувань, помноженої на ймовірність кожної події, помножену на -1:

$Cov(x_i,x_j)=-n\cdot p_i\cdot p_j\qquad i\neq j$

Створююча функція моменту для мультиноміального розподілу:

$\displaystyle \left(\sum_{i=1}^k p_ie^{t_i}\right) ^n$

Про автора

Редакція

Привіт, я Бенджамін, професор статистики на пенсії, який став викладачем статистики. Маючи великий досвід і знання в галузі статистики, я готовий поділитися своїми знаннями, щоб розширити можливості студентів через Statorials. Дізнайтеся більше