Чи впливають на інтерквартильний діапазон (iqr) викиди?

У статистиці ми часто хочемо знати, наскільки широко «розкидані» значення в розподілі.

Популярним способом вимірювання поширення є інтерквартильний діапазон , який обчислюється як різниця між першим квартилем і третім квартилем набору даних. Квартилі – це просто значення, які ділять набір даних на чотири рівні частини.

Приклад: Розрахунок інтерквартильного діапазону

У наступному прикладі показано, як обчислити інтерквартильний діапазон для даного набору даних:

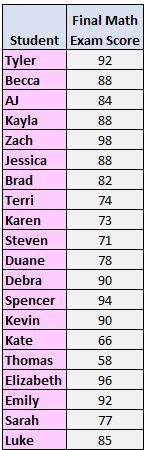
Крок 1: Розташуйте значення від найменшого до найбільшого.

58, 66, 71, 73, 74, 77, 78, 82, 84, 85, 88, 88, 88, 90, 90, 92, 92, 94, 96, 98

2. Знайдіть медіану.

58, 66, 71, 73, 74, 77 , 78, 82, 84, 85, 88, 88, 88, 90, 90, 92, 92, 94, 96, 98

У цьому випадку медіана становить від 85 до 88.

3. Медіана ділить набір даних на дві половини. Медіана нижньої половини є нижнім квартилем, а медіана верхньої половини є верхнім квартилем:

58, 66, 71, 73, 74 , 77, 78, 82, 84, 85, 88, 88, 88, 90, 90, 92, 92, 94, 96, 98

4. Обчисліть інтерквартильний діапазон.

У цьому випадку перший квартиль — це середнє значення двох середніх значень у нижній половині набору даних (75,5), а третій квартиль — це середнє значення двох середніх значень у верхній половині набору даних. (91).

Отже, інтерквартильний діапазон становить 91 – 75,5 = 15,5

Викиди не впливають на міжквартильний діапазон

Однією з причин, чому люди віддають перевагу використанню інтерквартильного діапазону (IQR) під час розрахунку «розповсюдження» набору даних, є те, що він стійкий до викидів. Оскільки IQR є просто середнім 50% діапазоном значень даних, на нього не впливають екстремальні викиди .

Щоб продемонструвати це, розглянемо такий набір даних:

[1, 4, 8, 11, 13, 17, 17, 20]

Ось різні показники поширення для цього набору даних:

• Інтерквартильний діапазон: 11
• Діапазон: 19
• Стандартне відхилення: 6,26
• Різниця: 39,23

Тепер розглянемо той самий набір даних, але з додаванням екстремального викиду:

[1, 4, 8, 11, 13, 17, 17, 20, 150 ]

Ось різні показники поширення для цього набору даних:

• Інтерквартильний діапазон: 12,5
• Діапазон: 149
• Стандартне відхилення: 43,96
• Спред: 1932,84

Зверніть увагу, як інтерквартильний діапазон змінюється лише незначно, від 11 до 12,5. Однак усі інші показники дисперсії різко змінюються.

Це демонструє, що на міжквартильний діапазон не впливають викиди, як на інші міри дисперсії. З цієї причини це надійний спосіб вимірювання розподілу середніх 50% значень у будь-якому розподілі.

Подальше читання:

Дисперсійні вимірювання
Калькулятор інтерквартильного діапазону