Нормальний розподіл

за Редакція 3 Серпня, 2023 Ймовірність 0 коментарів

У цій статті пояснюється, що таке нормальний розподіл у статистиці. Отже, ви знайдете визначення нормального розподілу, приклади нормального розподілу та властивості нормального розподілу.

Що таке нормальний розподіл?

Нормальний розподіл — це безперервний розподіл ймовірностей, графік якого має форму дзвона та симетричний відносно свого середнього. У статистиці нормальний розподіл використовується для моделювання явищ із дуже різними характеристиками, тому цей розподіл такий важливий.

Фактично, у статистиці нормальний розподіл вважається найважливішим розподілом із усіх розподілів ймовірностей, оскільки він не лише може моделювати велику кількість явищ реального світу, але нормальний розподіл також можна використовувати для наближення інших типів розподіли. за певних умов.

Символом нормального розподілу є велика літера N. Отже, щоб вказати, що змінна відповідає нормальному розподілу, вона позначається літерою N, а значення її середнього арифметичного та стандартного відхилення додаються в дужках.

$X\sim N(\mu,\sigma)$

Нормальний розподіл має багато різних назв, включаючи розподіл Гаусса , розподіл Гаусса та розподіл Лапласа-Гаусса .

Приклади нормального розподілу

Як правило, набори даних, які відповідають нормальному розподілу, містять велику кількість спостережень і охоплюють дуже загальні теми. Нижче наведено кілька прикладів статистичних вибірок, які загалом можна моделювати за допомогою нормального розподілу.

Приклади нормального розподілу:

Розмір студентів на курсі.
IQ працівників компанії.
Кількість бракованих деталей, вироблених на заводі за день.
Оцінки, отримані на іспиті студентами курсу.
Прибутковість акцій компаній, що котируються на біржі.

Графік нормального розподілу

Коли ми побачили, що таке нормальний розподіл і деякі приклади цього типу розподілу ймовірностей, давайте подивимося, як виглядає його графік, щоб краще зрозуміти концепцію.

На наступному графіку ви можете побачити, як змінюється функція щільності нормального розподілу в залежності від значень її середнього арифметичного та стандартного відхилення.

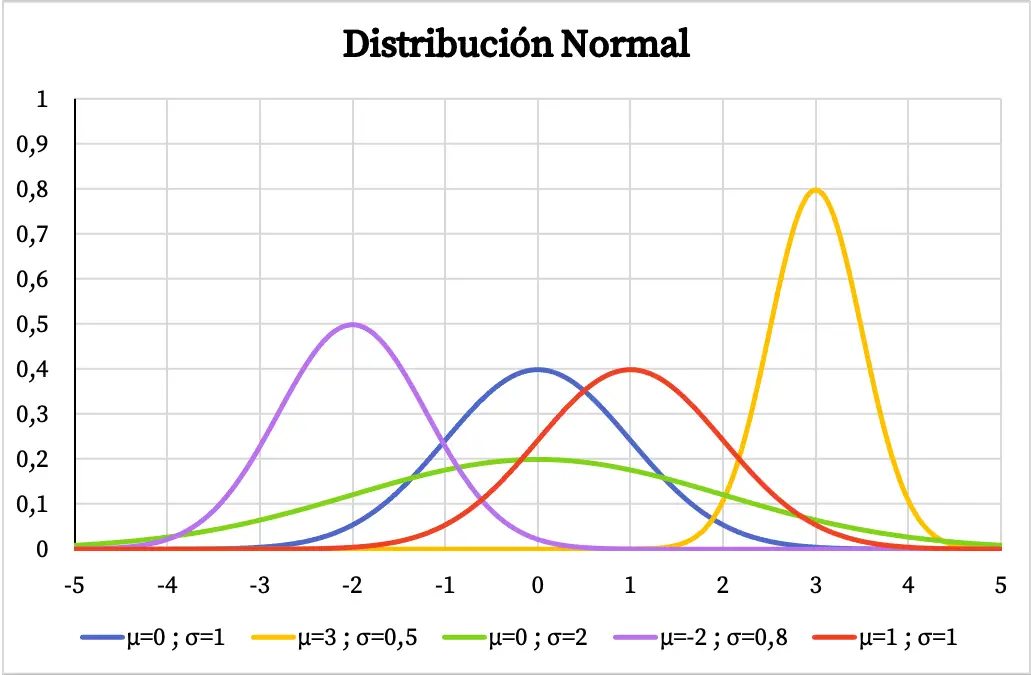
Маючи форму дзвона з центром на середньому арифметичному, якщо змінна має нормальний розподіл, це означає, що найбільше повторюване значення є середнім і що значення навколо середнього повторюються частіше, ніж крайні значення. Подібним чином, чим більше стандартне відхилення нормального розподілу, тим плоскіша форма його графічного представлення.

З іншого боку, графік кумулятивної функції ймовірності нормального розподілу також залежить від значень його середнього арифметичного та стандартного відхилення, як ви можете бачити на наступному зображенні:

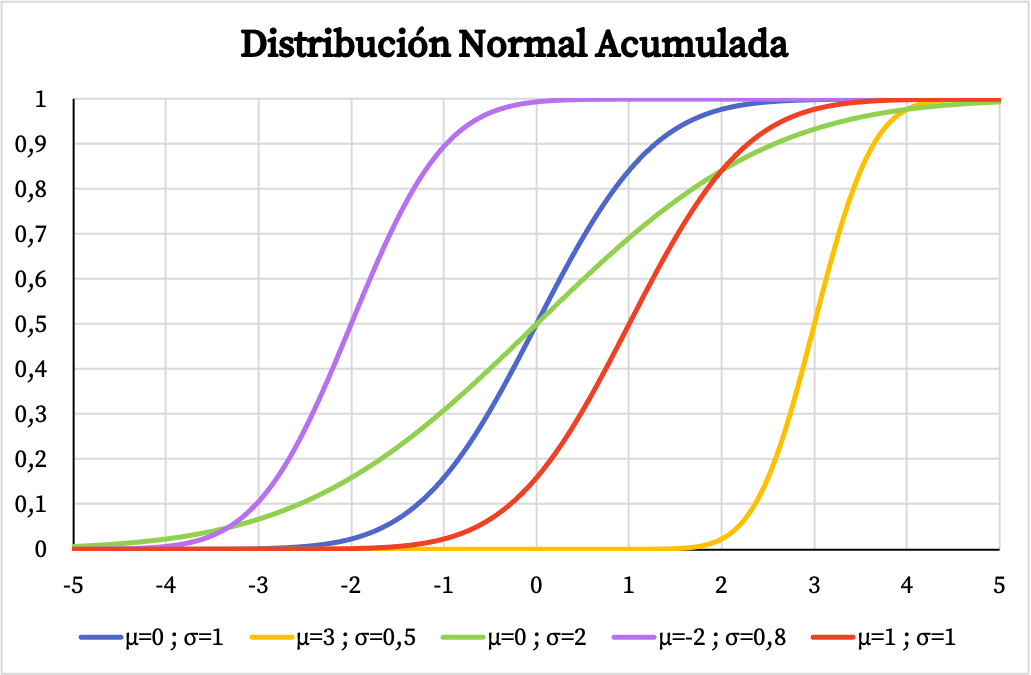
Функція щільності та функція розподілу нормального розподілу дозволяють розрахувати ймовірності, пов’язані з цим розподілом. Однак замість використання їхніх формул ви можете безпосередньо використовувати звичайні таблиці розподілу, оскільки це швидше. Ви можете переглянути ці таблиці за наступним посиланням:

➤ Див.: Таблиця нормального розподілу

Характеристика нормального розподілу

Нормальний розподіл має такі характеристики:

Нормальний розподіл залежить від двох характерних параметрів, якими є його середнє арифметичне (μ) і стандартне відхилення (σ).

$X\sim N(\mu,\sigma)$

Нормальний розподіл може приймати додатні та від’ємні значення, тому область визначення нормального розподілу складається з дійсних чисел.

$x\in \mathbb{R}$

Медіана і мода нормального розподілу дорівнюють середньому арифметичному розподілу.

$Me=Mo=\mu$

Коефіцієнт асиметрії та коефіцієнт ексцесу нормального розподілу дорівнюють нулю.

$\begin{array}{c}A=0\\[2ex]C=0\end{array}$

Формула для функції густини нормального розподілу:

$\displaystyle P[X=x]=\frac1{\sigma\sqrt{2\pi}}\; e^{ - \frac{(x-\mu)^2}{2\sigma^2}}$

Подібним чином формула для кумулятивної функції ймовірності нормального розподілу має вигляд:

$\displaystyle P[X\leq x]=\frac{1}{\sigma\sqrt{2\pi}}\int_{-\infty}^x e^{-\frac{(x - \mu)^2}{2\sigma^2}}\, dx ,\quad x\in\mathbb{R}$

Застосування центральної граничної теореми полягає в тому, що розподіл Пуассона може апроксимувати нормальний розподіл, якщо значення λ є достатньо великим.

$\text{Poisson}(\lambda)\ \color{orange}\bm{\longrightarrow}\color{black} \ N\left(\lambda, \sqrt{\lambda}\right)$

Інше застосування центральної граничної теореми полягає в тому, що біноміальний розподіл може бути апроксимований нормальним розподілом для наборів даних із великою кількістю спостережень.

$\text{Bin}(n,p)\ \color{orange}\bm{\longrightarrow}\color{black} \ N\left(n\cdot p, \sqrt{n\cdot p \cdot (1-p)}\right)$

Стандартний нормальний розподіл

Стандартний нормальний розподіл , який також називають одиничним нормальним розподілом , є найпростішим випадком нормального розподілу. Точніше, стандартний нормальний розподіл – це нормальний розподіл із середнім значенням і стандартним відхиленням, що дорівнює 0 і 1 відповідно.

$\displaystyle N(0,1) \ \color{orange}\bm{\longrightarrow}\color{black}\begin{cases} \mu=0\\[2ex]\sigma=1\end{cases}$

Зауважте, що будь-який нормальний розподіл можна перетворити на стандартний нормальний розподіл шляхом застосування процесу, який називається типуванням, який передбачає віднімання його середнього арифметичного від кожного значення, а потім ділення на його стандартне відхилення.

Крім того, стандартний нормальний розподіл використовується для визначення будь-якої ймовірності нормального розподілу за допомогою його таблиці ймовірностей. Отже, щоб знайти ймовірність нормального розподілу, спочатку вводиться змінна, щоб перетворити її на стандартний нормальний розподіл, а потім ми дивимося в таблицю, щоб побачити відповідне значення ймовірності. Щоб дізнатися більше, натисніть на таке посилання:

➤ Див.: Стандартний нормальний розподіл