Як розрахувати r-квадрат вручну
У статистиці R квадрат (R 2 ) вимірює частку дисперсії у змінній відповіді , яку можна пояснити змінною предиктором у регресійній моделі.
Ми використовуємо наступну формулу для обчислення R у квадраті:
R 2 = [ (nΣxy – (Σx)(Σy)) / (√ nΣx 2 -(Σx) 2 * √ nΣy 2 -(Σy) 2 ) ] 2
У наведеному нижче покроковому прикладі показано, як вручну обчислити R-квадрат для даної моделі регресії.
Крок 1: Створіть набір даних
Спочатку створимо набір даних:
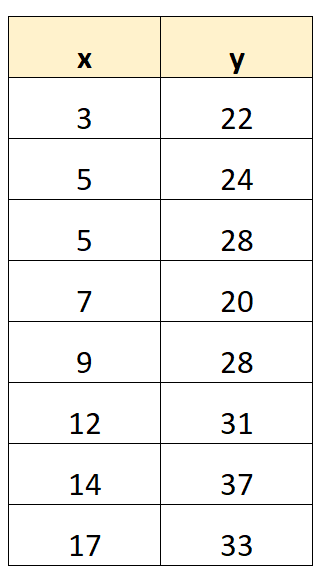
Крок 2: Обчисліть необхідні показники
Далі обчислимо кожен показник, який потрібно використовувати у формулі R2 :
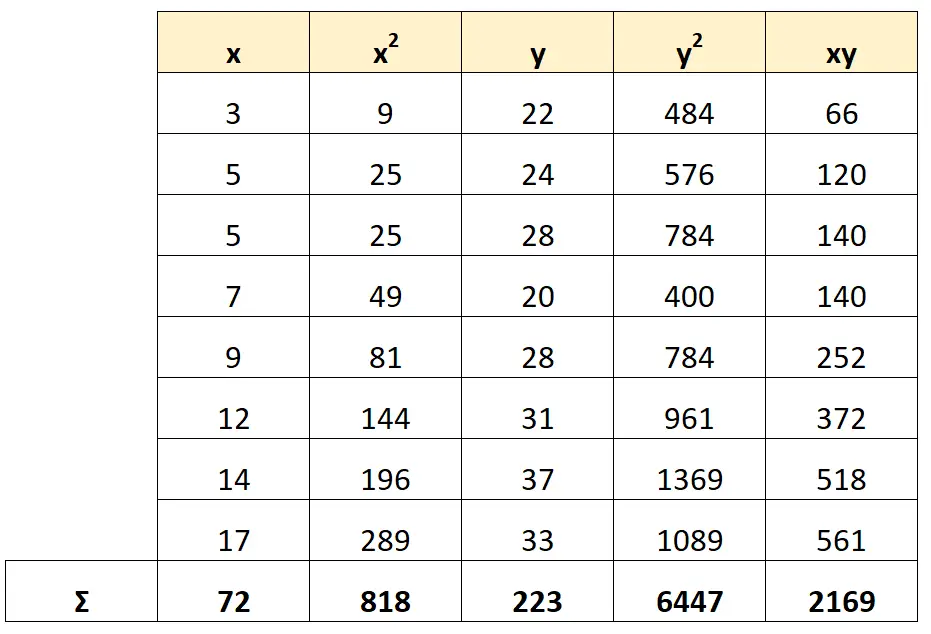
Крок 3: обчисліть R у квадраті
Нарешті, ми інтегруємо кожну метрику у формулу для R 2 :
- R 2 = [ (nΣxy – (Σx)(Σy)) / (√ nΣx 2 -(Σx) 2 * √ nΣy 2 -(Σy) 2 ) ] 2
- R 2 = [ (8*(2169) – (72)(223)) / (√ 8*(818)-(72) 2 * √ 8*(6447)-(223) 2 ) ] 2
- R2 = 0,6686
Примітка: n у формулі представляє кількість спостережень у наборі даних і в цьому прикладі виявляється n = 8 спостережень.
Якщо припустити, що x є змінною прогнозу, а y є змінною відповіді в цій моделі регресії, R-квадрат моделі дорівнює 0,6686 .
Це говорить нам про те, що 66,86% варіації змінної y можна пояснити змінною x .
Додаткові ресурси
Вступ до простої лінійної регресії
Вступ до множинної лінійної регресії
R проти R-Square: у чому різниця?
Що таке хороше значення R-квадрат?
Про автора
Редакція
Привіт, я Бенджамін, професор статистики на пенсії, який став викладачем статистики. Маючи великий досвід і знання в галузі статистики, я готовий поділитися своїми знаннями, щоб розширити можливості студентів через Statorials. Дізнайтеся більше