Три гіпотези, сформульовані в парному t-критерії

Т-критерій для парних вибірок використовується для порівняння середніх значень двох вибірок, коли кожне спостереження в одній вибірці можна пов’язати зі спостереженням в іншій вибірці.

Цей тип перевірки робить такі припущення щодо даних:

1. Незалежність: кожне спостереження має бути незалежним від будь-якого іншого спостереження.

2. Нормальність: відмінності між парами мають бути приблизно нормально розподілені.

3. Жодних екстремальних викидів: у відмінностях не повинно бути екстремальних викидів.

Якщо одне або декілька з цих припущень не виконуються, результати t-критерію для парних зразків можуть бути ненадійними або вводити в оману.

У цьому підручнику ми надаємо пояснення кожного припущення, як визначити, чи виконується припущення, і що робити, якщо воно порушується.

Гіпотеза 1: Незалежність

Т-критерій парних вибірок передбачає, що кожне спостереження не залежить від усіх інших спостережень.

Як перевірити цю гіпотезу

Найпростіший спосіб перевірити це припущення полягає в тому, щоб перевірити, що кожне спостереження було зібрано за допомогою методу випадкової вибірки .

Якщо використовувався метод випадкової вибірки (наприклад, проста випадкова вибірка), ми можемо припустити, що кожне спостереження не залежить від усіх інших спостережень.

Що робити, якщо це припущення не виконується

Якщо це припущення не виконується, результати t-критерію для парних зразків є повністю недійсними.

У цьому сценарії найкраще збирати нові спостереження за допомогою методу випадкової вибірки, щоб переконатися, що кожне спостереження є незалежним.

Гіпотеза 2: нормальність

Т-критерій парних вибірок передбачає, що відмінності між парами мають бути приблизно нормально розподілені.

Це важливе припущення, тому що якщо відмінності між парами розподілені неправильно, використовувати p-значення тесту для висновків не можна.

Як перевірити цю гіпотезу

Найпростіший спосіб перевірити цю гіпотезу — просто створити гістограму парних відмінностей і візуально перевірити, чи має гістограма форму дзвона.

Наприклад, якщо гістограма виглядає так, ми б сказали, що виконано припущення про нормальність:

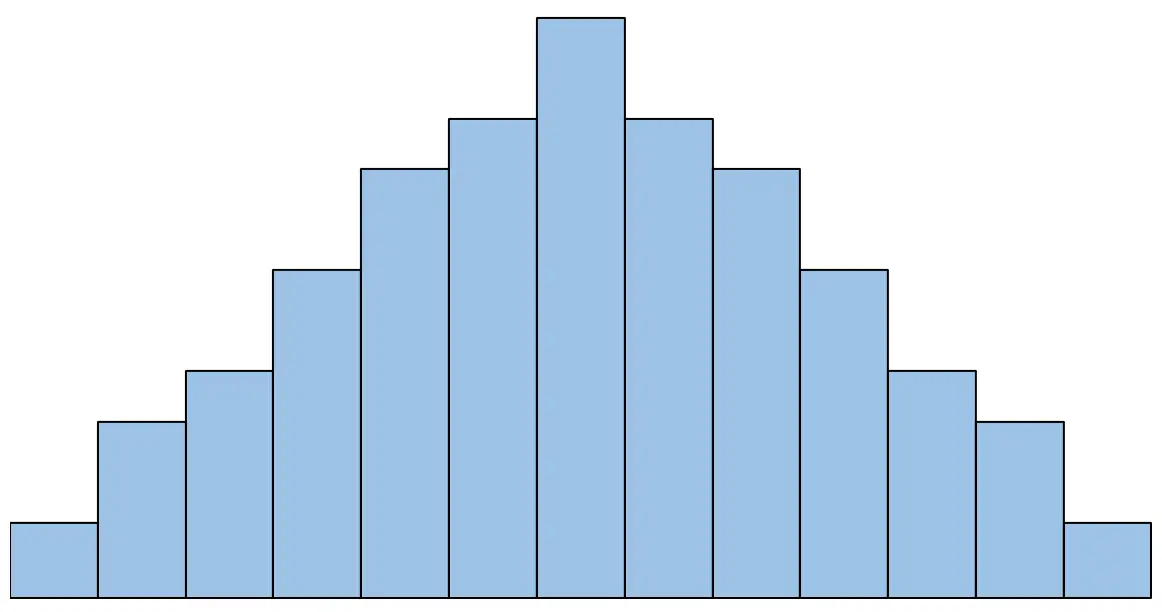
Однак, якщо гістограма виглядає так, ми б сказали, що припущення нормальності не виконується:

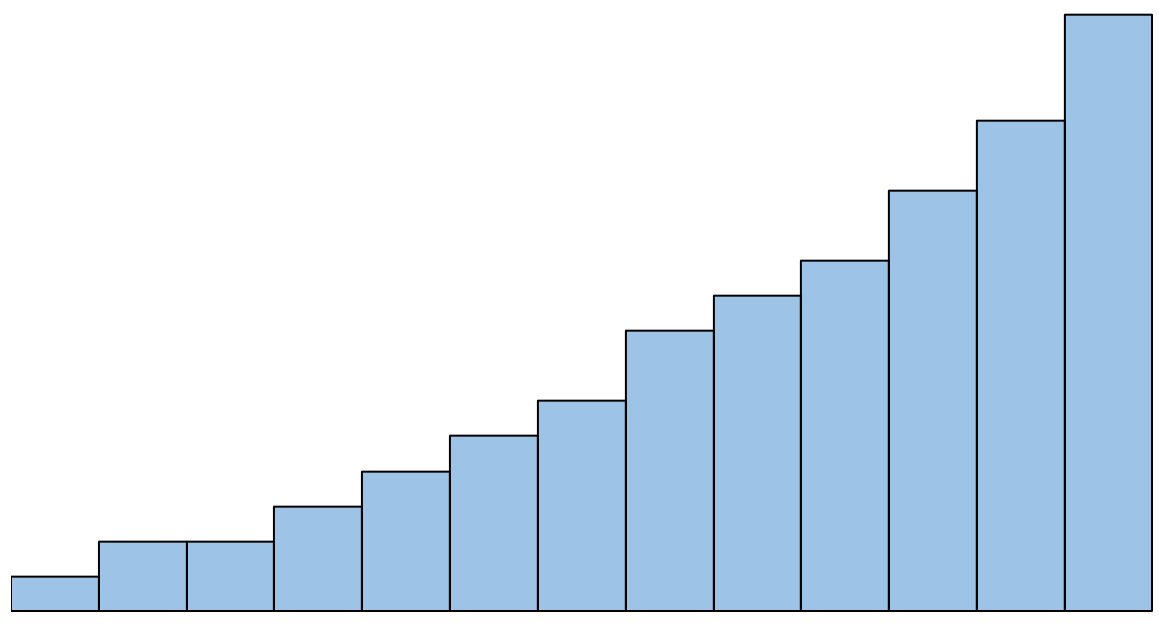
Що робити, якщо це припущення не виконується

Якщо це припущення порушується, ми можемо виконати критерій рангу Вілкоксона зі знаком , який вважається непараметричним еквівалентом t-критерію парних вибірок і не передбачає, що парні різниці розподілені нормально.

Гіпотеза 3: екстремальних викидів немає

Т-критерій для парних вибірок передбачає, що в даних немає екстремальних викидів.

Як перевірити цю гіпотезу

Найпростіший спосіб перевірити цю гіпотезу — створити коробковий графік парних відмінностей і візуально перевірити, чи є викиди.

Наприклад, припустімо, що коробковий графік парних відмінностей виглядає так:

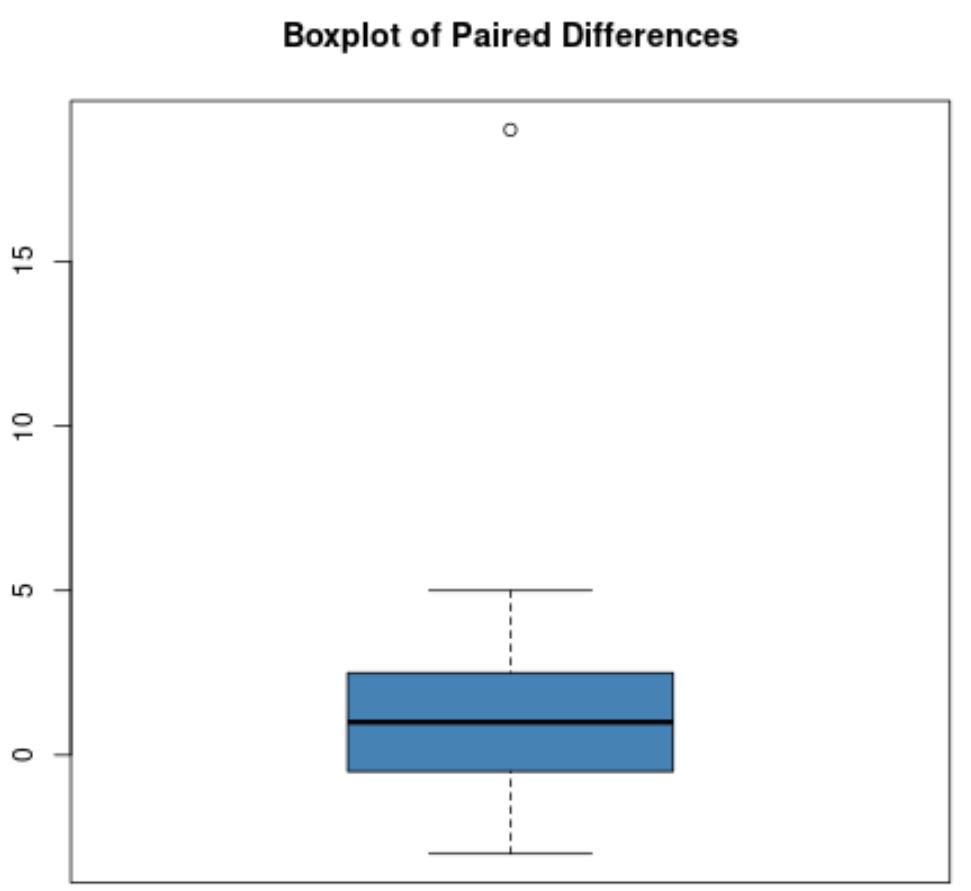
Більшість парних відмінностей близькі до нуля, але є одна парна різниця, що дорівнює приблизно 19, що явно викидається.

Примітка . Круг зазвичай використовується на прямокутному графіку для позначення викиду.

Однак припустімо, що коробковий графік парних відмінностей виглядає так:

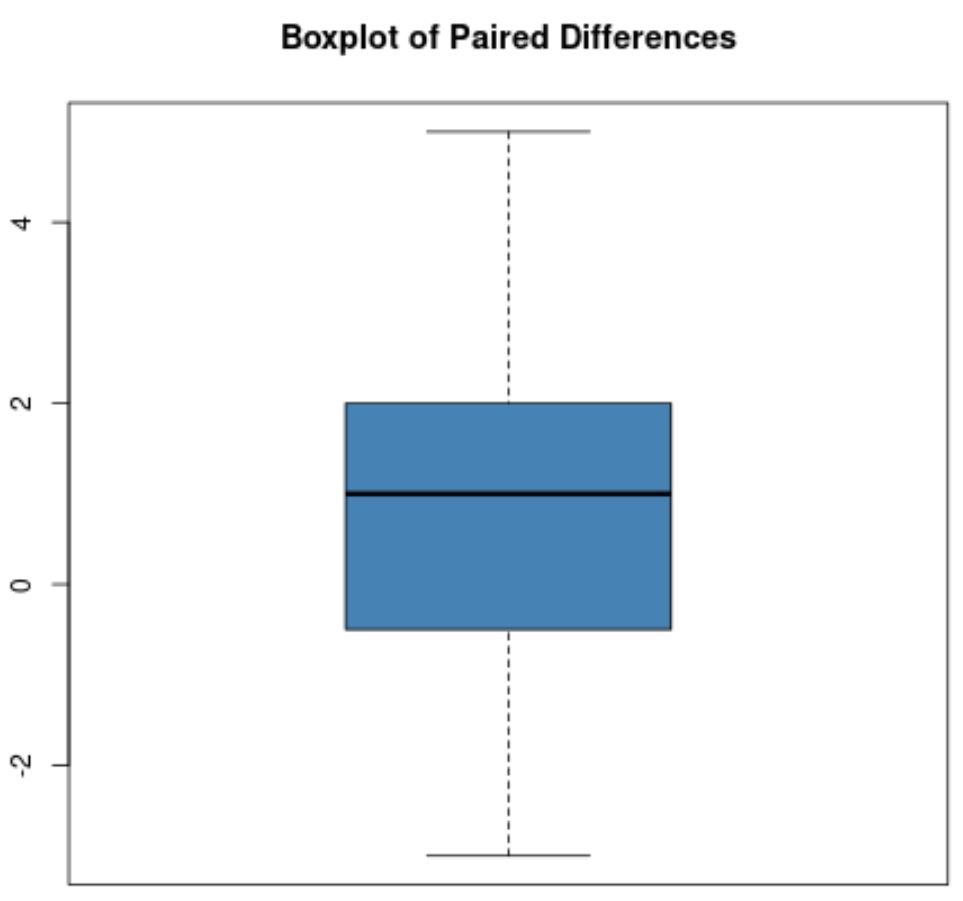
На цій коробковій діаграмі немає чітких викидів, тому ми припустимо, що в даних немає екстремальних викидів.

Що робити, якщо це припущення не виконується

Якщо це припущення порушується, на результати t-критерію для парних зразків може аномально вплинути викид.

У цьому випадку ви можете видалити викид, якщо вважаєте, що він представляє помилкову точку даних або є результатом помилки введення даних.

Крім того, ви можете зберегти викид і просто зазначити його під час звітування про результати t-критерію для парних зразків.

Додаткові ресурси

Наступні навчальні посібники пояснюють припущення, зроблені в інших статистичних тестах:

Чотири гіпотези, сформульовані в t-критерії
Чотири гіпотези тесту хі-квадрат
Чотири гіпотези параметричних тестів