Три припущення повторних вимірювань anova

Дисперсійний аналіз повторних вимірювань використовується, щоб визначити, чи існує статистично значуща різниця між середніми значеннями трьох або більше груп, у яких одні й ті самі суб’єкти з’являються в кожній групі.

Однак перед виконанням повторних вимірювань ANOVA ми повинні переконатися, що виконуються такі припущення:

1. Незалежність: кожне спостереження має бути незалежним.

2. Нормальність: розподіл змінної відповіді є нормальним.

3. Сферичність: дисперсії відмінностей між усіма комбінаціями споріднених груп мають бути рівними.

Якщо одне або декілька з цих припущень порушуються, результати повторних вимірювань ANOVA можуть бути ненадійними.

У цій статті ми надаємо пояснення для кожного припущення, як визначити, чи виконується припущення, і що робити, якщо воно не виконується.

Гіпотеза 1: Незалежність

Повторний ANOVA передбачає, що кожне спостереження у вашому наборі даних не залежить від усіх інших спостережень.

Як визначити, чи виконується це припущення

Найпростіший спосіб перевірити це припущення полягає в тому, щоб перевірити, що кожна особа в наборі даних була випадково відібрана з популяції за допомогою методу випадкової вибірки .

Якщо використовувався метод випадкової вибірки, кожне спостереження можна вважати незалежним.

Що робити, якщо це припущення не виконується

Якщо це припущення не виконується, то це є серйозною проблемою, оскільки цінності кожної людини можуть бути пов’язані між собою тим чи іншим чином.

Часто єдиним виходом у цьому сценарії є залучення осіб для нового дослідження за допомогою методу випадкової вибірки.

Гіпотеза 2: нормальність

Повторні вимірювання ANOVA припускають, що розподіл змінної відповіді є нормальним .

Як визначити, чи виконується це припущення

Є два способи перевірити, чи вірна ця гіпотеза:

1. Створіть гістограму або графік QQ

Ви можете візуально перевірити, чи є розподіл змінної відповіді приблизно нормальним, створивши гістограму або графік QQ.

Якщо ви створюєте гістограму , просто переконайтеся, що розподіл змінної відповіді приблизно має форму дзвона. Якщо так, ви часто можете припустити, що припущення про нормальність виконується:

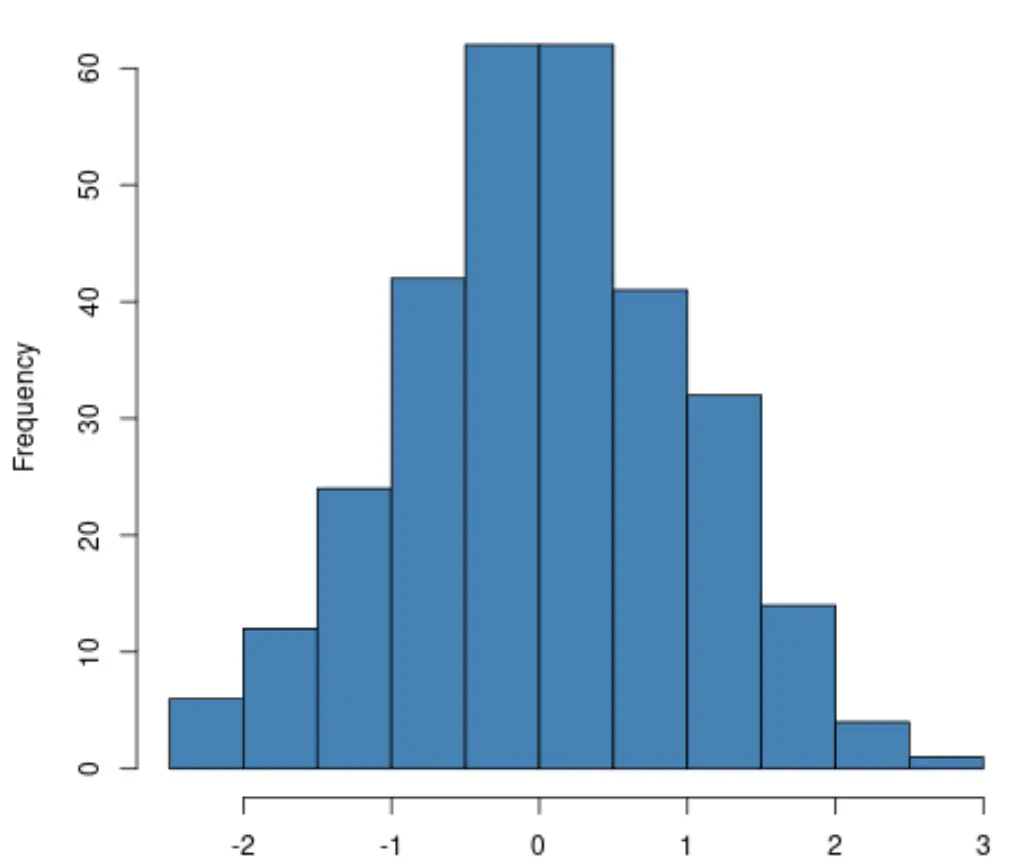
Якщо ви створюєте діаграму QQ , перевірте, чи точки даних лежать уздовж прямої діагональної лінії. Якщо так, ви можете загалом вважати, що припущення про нормальність виконується:

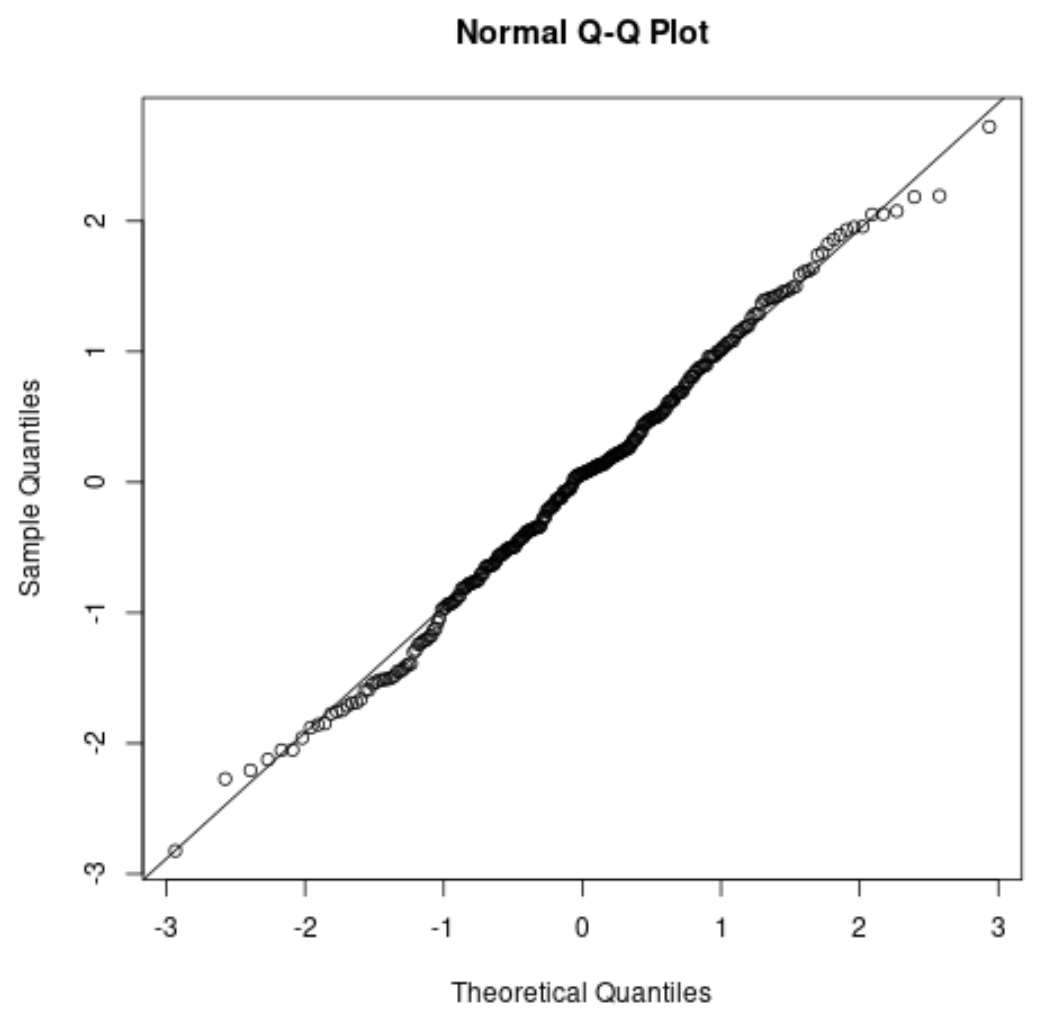
Пов’язане: Як використовувати графіки QQ для перевірки нормальності

2. Виконайте формальний статистичний тест

Ви також можете виконати тест Шапіро-Вілка, щоб перевірити нормальність. Якщо p-значення тесту менше 0,05, це означає, що дані розподілені неправильно.

Однак майте на увазі, що під час роботи з надзвичайно великими вибірками статистичні тести, такі як тест Шапіро-Вілка, майже завжди повідомлять вам, що ваші дані не є нормальними.

З цієї причини часто найкраще візуально перевіряти дані за допомогою таких діаграм, як гістограми та графіки QQ. Просто подивившись на графіки, ви можете отримати гарне уявлення про те, чи дані розподіляються нормально чи ні.

Що робити, якщо це припущення не виконується

Загалом, дисперсійний аналіз повторних вимірювань вважається досить надійним проти порушень припущення про нормальність, якщо розміри вибірки достатньо великі.

Якщо припущення про нормальність серйозно порушено, у вас є два варіанти:

1. Перетворіть значення відповіді ваших даних, щоб розподіли були більш нормально розподілені.

2. Виконайте еквівалентний непараметричний тест, такий як тест Фрідмана , який не вимагає припущення нормальності.

Припущення 3: Сферичність

Дисперсійний аналіз повторних вимірювань передбачає сферичність , тобто дисперсії відмінностей між усіма комбінаціями споріднених груп мають бути рівними.

Якщо це припущення не виконується, коефіцієнт F стає завищеним, а результати повторних вимірювань ANOVA стають ненадійними.

Як визначити, чи виконується це припущення

Щоб перевірити, чи виконується це припущення, ми можемо виконати тест сферичності за Моклі.

Цей тест використовує таку нульову та альтернативну гіпотезу:

• H ₀ : Дисперсії різниць рівні
• H _A : Дисперсії відмінностей не рівні

Якщо p-значення тесту нижче певного рівня значущості (наприклад, α = 0,05), тоді ми відхиляємо нульову гіпотезу та робимо висновок, що дисперсії відмінностей не рівні.

В іншому випадку, якщо p-значення не менше за певний рівень значущості (наприклад, α = 0,05), ми не можемо відхилити нульову гіпотезу та робимо висновок, що припущення про сферичність виконується.

Залежно від статистичного програмного забезпечення, яке ви використовуєте, результати цього тесту виглядатимуть так:

Оскільки p-значення не менше ніж 0,05, ми не зможемо відхилити нульову гіпотезу та зробити висновок, що припущення про сферичність виконується в цьому конкретному прикладі.

Що робити, якщо це припущення не виконується

Якщо ми відкидаємо нульову гіпотезу тесту сферичності Моклі, ми зазвичай застосовуємо поправку до ступенів свободи, які використовуються для обчислення значення F у таблиці ANOVA повторних вимірювань.

Ми можемо застосувати три виправлення:

• Гюйн-Фельдт (найменш консервативний)
• Серр–Гайсер
• Нижня межа (найбільш консервативна)

Кожна з цих поправок має тенденцію до збільшення p-значень у вихідній таблиці ANOVA для повторних вимірювань, щоб врахувати той факт, що припущення про сферичність порушується.

Потім ми можемо використовувати ці p-значення, щоб визначити, чи слід нам відхиляти нульову гіпотезу повторних вимірювань ANOVA.

Додаткові ресурси

У наступних посібниках надається додаткова інформація про дисперсійний аналіз повторних вимірювань:

Вступ до дисперсійного аналізу повторних вимірювань
Калькулятор повторних вимірювань ANOVA
Як звітувати про результати повторних вимірювань ANOVA
Односторонній дисперсійний аналіз і дисперсійний аналіз повторних вимірювань: різниця