Як порівняти гістограми (з прикладами)

Гістограма – це тип діаграми, який дозволяє візуалізувати розподіл значень у наборі даних.

На осі X відображаються значення набору даних, а на осі Y – частота кожного значення.

Гістограми корисні, оскільки вони дозволяють нам швидко зрозуміти розподіл значень у наборі даних. Вони також корисні для порівняння двох різних наборів даних.

Порівнюючи дві або більше гістограм, ми можемо відповісти на три різні запитання:

1. Як порівнюють медіанні значення?

Ми можемо приблизно оцінити, що медіана лежить поблизу середини кожної гістограми, що дозволяє нам порівнювати медіанні значення розподілів.

2. Як порівняти дисперсію?

Ми можемо візуально побачити, яка гістограма більш розкидана, що дає нам уявлення про те, який розподіл має більш розсіяні значення.

3. Як порівнюється асиметрія?

Якщо гістограма має «хвіст» у лівій частині графіка, це означає, що вона має негативний перекіс. І навпаки, якщо гістограма має «хвіст» на правій стороні графіка, кажуть, що вона позитивно викривлена. Ми можемо візуально перевірити кожну гістограму, щоб порівняти асиметрію .

У наступному прикладі показано, як порівняти дві різні гістограми та відповісти на ці три запитання.

Приклад: порівняння гістограм

Припускається, що 200 студентів використовують один метод навчання для підготовки до іспиту, а інші 200 студентів використовують інший метод навчання для підготовки до того самого іспиту.

Припустімо, ми створюємо такі гістограми для порівняння результатів іспитів кожної групи студентів:

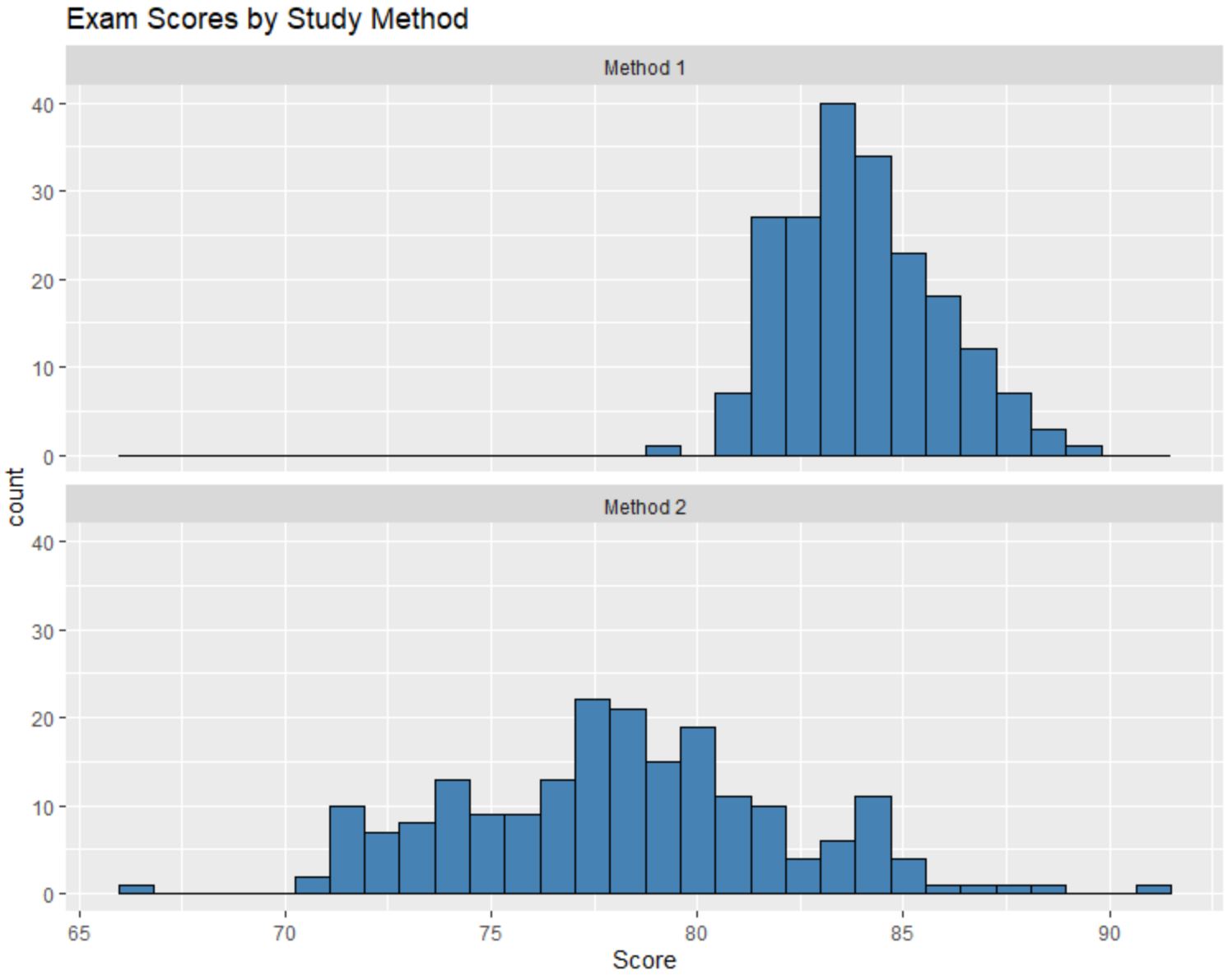
Ми можемо порівняти ці гістограми та відповісти на такі три запитання:

1. Як порівнюють медіанні значення?

Хоча ми не знаємо точних середніх значень кожного розподілу, просто дивлячись на гістограми, очевидно, що середній бал студентів, які використовували Метод 1, вищий, ніж середній бал студентів, які використовували Метод 1. спосіб 2 .

Ми могли б оцінити, що середнє значення для методу 1 становить приблизно 84, а середнє значення для методу 2 – близько 78.

2. Як порівняти дисперсію?

Значення гістограми для методу 2 набагато більш розкидані, ніж для методу 1, що говорить нам про те, що існує набагато більша дисперсія в результатах іспитів для студентів, які використовували метод 2.

3. Як порівнюється асиметрія?

Дивлячись на гістограми, здається, що розподіл тестових балів для методу 1 трохи зміщений вправо, на що вказує «хвіст», що тягнеться праворуч від гістограми.

Однак у розподілі результатів іспиту для методу 2 немає «хвоста», який говорить нам про те, що розподіл незначний або не спотворений.

Бонус : Ось код, який ми використовували в R для створення цих двох гістограм:

 library (ggplot2)

#make this example reproducible
set. seeds (0)

#create data frame
df <- data. frame (method=rep(c(' Method 1 ', ' Method 2 '), each= 200 ),
                 Score=c(rnorm( 200 , mean= 84 , sd= 2 ),
                         rnorm( 200 , mean= 78 , sd= 4 )))

#create histogram of scores for each method
ggplot(df, aes(x=Score)) +
  geom_histogram(fill=' steelblue ', color=' black ') +
  facet_wrap(.~method, nrow= 2 ) +
  labs(title=' Exam Scores by Study Method ')

Додаткові ресурси

У наступних посібниках пояснюється, як виконувати інші типові завдання за допомогою гістограм:

Як оцінити середнє та медіану будь-якої гістограми
Як оцінити стандартне відхилення будь-якої гістограми
Як описати форму гістограм