Правило додавання (або правило додавання)

У цій статті пояснюється, що таке правило додавання, також відоме як правило додавання, і для чого воно використовується в ймовірності та статистиці. Крім того, ви зможете побачити формулу правила додавання та розв’язати вправи, які показують, як її використовувати.

Що таке правило додавання (або правило додавання)?

Правило додавання (або правило додавання ) стверджує, що сума ймовірностей двох подій дорівнює сумі ймовірностей кожної окремої події мінус ймовірність того, що обидві події відбудуться одночасно.

Отже, формула для правила додавання P(A⋃B)=P(A)+P(B)−P(A⋂B).

Таким чином, щоб додати дві ймовірності, ми не можемо просто додати кожну ймовірність, оскільки ми також повинні відняти член, який представляє спільну ймовірність двох подій. Однак у деяких випадках лише шляхом додавання ймовірності кожної події можна отримати правильний результат суми ймовірностей. Нижче ми побачимо, що це за випадки.

Коротше кажучи, правило додавання використовується для обчислення ймовірності настання тієї чи іншої події, тобто ймовірності того, що відбудеться принаймні одна з двох можливих подій.

Формула правила додавання

Правило додавання говорить, що для обчислення ймовірності настання події A чи події B ми повинні додати ймовірність настання події A плюс ймовірність настання події B і відняти ймовірність того, що обидві події відбудуться одночасно. .

Тому формула правила додавання (або правила додавання) виглядає наступним чином:

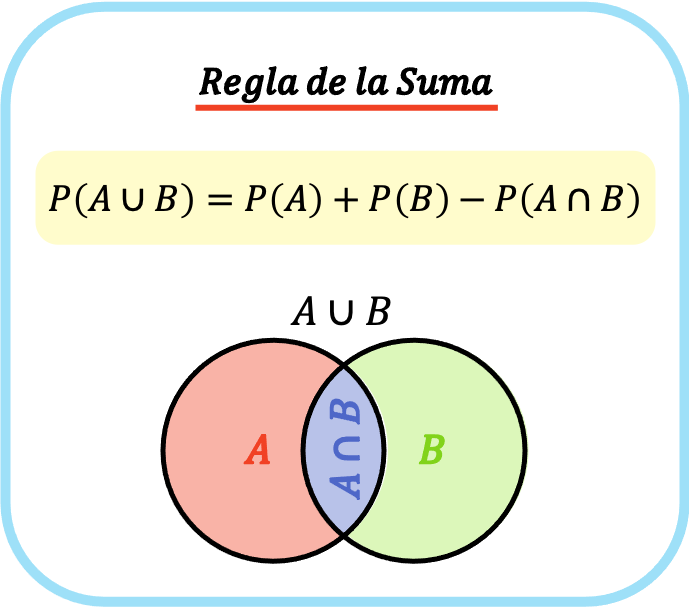
золото:

• 

  це ймовірність події А або події В.

• 

  це ймовірність того, що подія А відбудеться.

• 

  це ймовірність того, що подія B відбудеться.

• 

  це спільна ймовірність того, що події A та B відбудуться.

Тому, щоб використовувати правило суми, вам потрібно знати, як обчислити спільну ймовірність двох подій. Ви можете побачити, як це робиться, за наступним посиланням:

Приклад правила суми для ексклюзивних подій

Щоб завершити розуміння концепції, давайте розглянемо приклад застосування правила додавання.

• Ми поклали в ящик 10 синіх куль, 6 помаранчевих і 4 зелених кульки. Яка ймовірність витягнути синю або оранжеву кульку?

У вправі нам пропонується визначити ймовірність того, що відбудеться та чи інша подія. Тому для розв’язування задачі потрібно використати формулу правила додавання:

Отже, ми спочатку обчислюємо ймовірність кожної події окремо, використовуючиправило Лапласа :

Однак у цьому випадку обидві події не можуть відбуватися одночасно, оскільки це дві взаємовиключні події . Отже, якщо ми намалюємо синю кулю, ми більше не зможемо намалювати помаранчеву кулю, і навпаки.

Отже, спільна ймовірність обох подій дорівнює нулю, а отже формула правила суми спрощена:

Отже, розрахунок ймовірності зловити синю або помаранчеву кулю виглядає наступним чином:

Коротше кажучи, ймовірність витягнути синю або помаранчеву кульку з коробки становить 80%.

Приклад правила додавання для невиключних подій

Побачивши конкретний приклад правила додавання, коли події є виключними, ми тепер побачимо, як цей закон використовується, коли події є невиключними.

• Якщо ми підкинемо монету двічі, яка ймовірність отримати голови принаймні в одному підкиданні?

У цьому випадку події не є взаємовиключними, оскільки ми можемо отримати «голови» під час першого кидка та «решки» під час другого кидка. Тому формула правила додавання не є спрощеною і виглядає наступним чином:

Отже, спочатку нам потрібно обчислити ймовірність отримання «голов» під час підкидання монети, застосувавши правило Лапласа:

Крім того, дві події незалежні, тому ми можемо обчислити спільну ймовірність двох подій за правилом добутку :

Нарешті, щоб знайти ймовірність того, що голови випадуть принаймні в одному з двох кидків, просто підставте значення у формулу правила додавання та виконайте обчислення:

Підсумовуючи, ймовірність того, що двічі підкинувши монету, принаймні один раз випаде орел, становить 75%.