Гіпотеза постійної дисперсії: визначення та приклад
Лінійна регресія – це техніка, яку ми використовуємо для кількісного визначення зв’язку між однією або декількома змінними прогнозу та змінною відповіді .
Одним із ключових припущень лінійної регресії є те, що залишки мають постійну дисперсію на кожному рівні змінної (змінних) предиктора.
Якщо це припущення не перевірено, залишки будуть страждати від гетероскедастичності . Коли це відбувається, оцінки коефіцієнтів моделі стають ненадійними.
Як оцінити постійну дисперсію
Найпоширеніший спосіб визначити, чи мають залишки регресійної моделі постійну дисперсію, полягає в створенні графіка підігнаних значень проти залишків .
Це тип графіка, який відображає підігнані значення регресійної моделі вздовж осі X і залишки цих значень, підігнані вздовж осі Y.
Якщо розподіл залишків приблизно однаковий на кожному рівні підігнаних значень, ми говоримо, що припущення постійної дисперсії виконано.
В іншому випадку, якщо дисперсія залишків систематично збільшується або зменшується, це припущення, швидше за все, порушується.
Примітка . Цей тип графіка можна створити лише після підгонки регресійної моделі до набору даних.
На наступній діаграмі показано приклад графіка підігнаних значень проти залишків, який відображає постійну дисперсію :
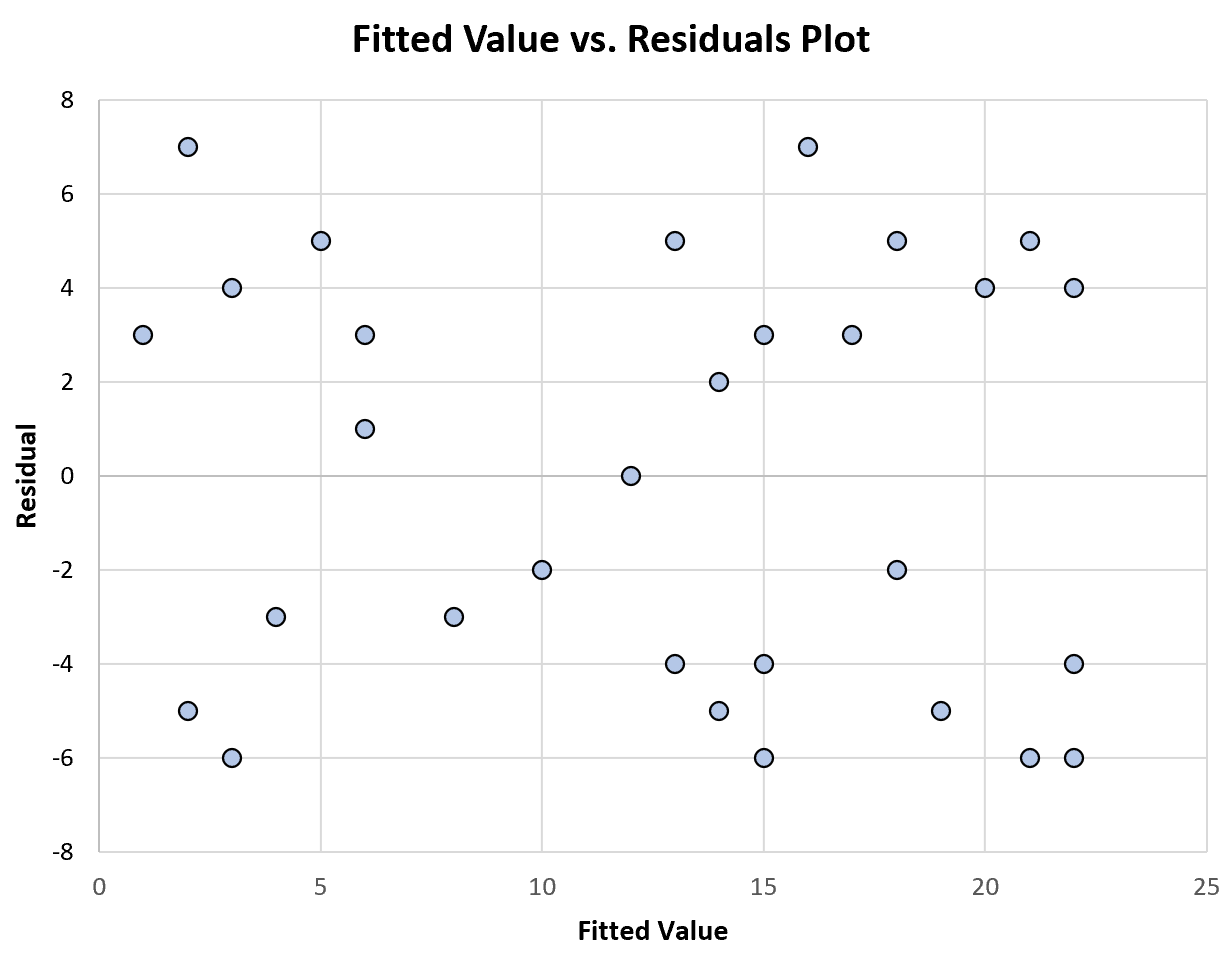
Зверніть увагу на те, як залишки випадковим чином розкидані навколо нуля, без певної моделі, з приблизно постійною дисперсією на кожному рівні підігнаних значень.
На наступній діаграмі показано приклад графіка підігнаних значень проти залишків, який відображає непостійну дисперсію :
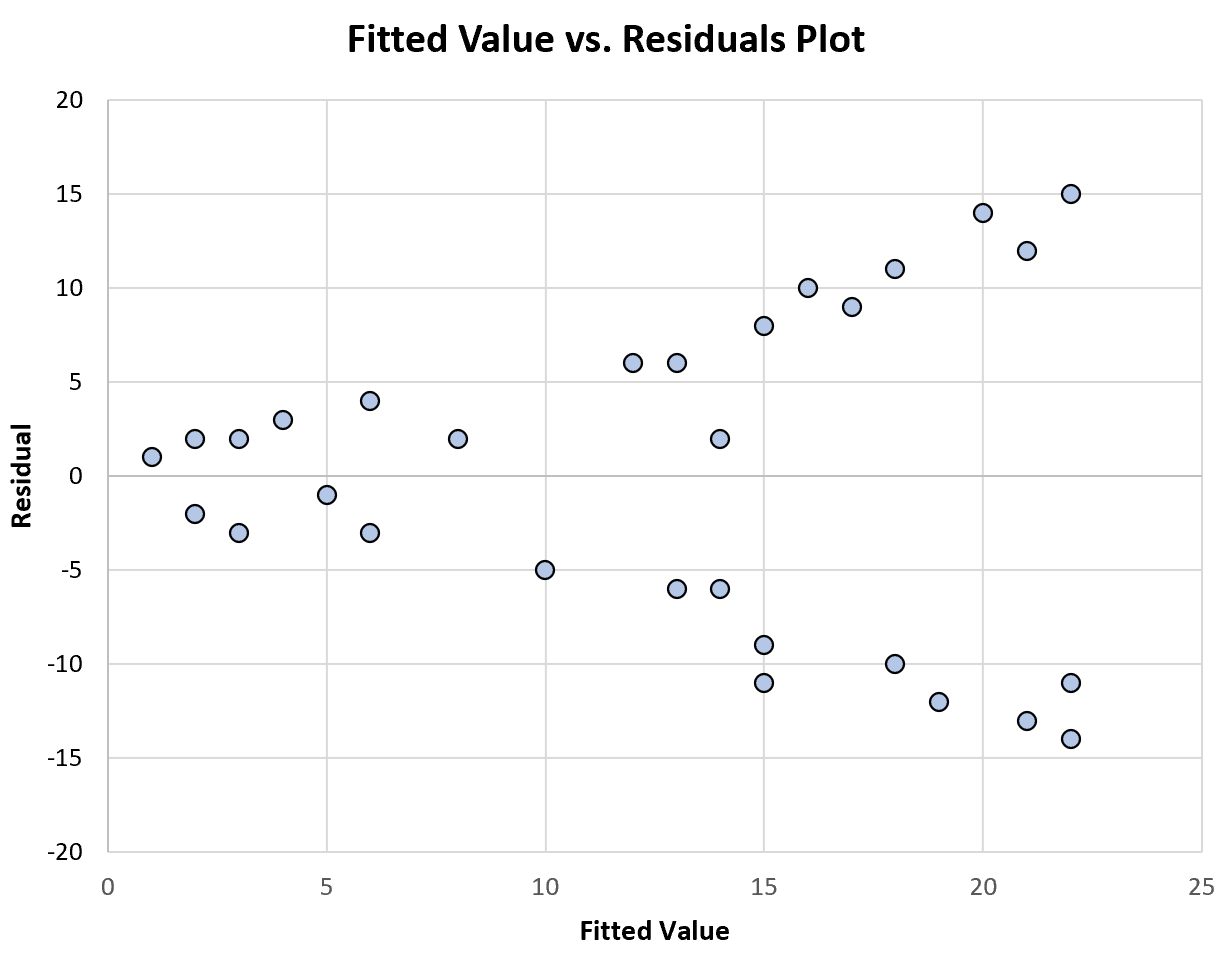
Зауважте, що розподіл залишків стає більшим із збільшенням підігнаних значень. Це типова ознака непостійної дисперсії.
Це говорить нам про те, що наша модель регресії страждає від непостійної дисперсії в залишках і що оцінки коефіцієнтів моделі тому ненадійні.
Як виправити порушення постійної дисперсії
Якщо припущення постійної дисперсії порушується, найпоширенішим способом вирішення цієї проблеми є перетворення змінної відповіді за допомогою одного з трьох перетворень:
1. Перетворення журналу: перетворення змінної відповіді з y на log(y)
2. Перетворення квадратного кореня: перетворення змінної відповіді з y на √y
3. Перетворення кубічного кореня: перетворення змінної відповіді з y на y 1/3
Виконуючи ці перетворення, проблема непостійної дисперсії загалом зникає.
Додаткові ресурси
У наступних посібниках надається додаткова інформація про лінійну регресію та залишковий аналіз.
Вступ до простої лінійної регресії
Вступ до множинної лінійної регресії
Чотири припущення лінійної регресії
Що таке залишки в статистиці?