Розподіл хі-квадрат

за Редакція 4 Серпня, 2023 Ймовірність 0 коментарів

У цій статті пояснюється, що таке розподіл хі-квадрат і для чого він використовується. Крім того, ви знайдете графік розподілу хі-квадрат і його властивості.

Що таке розподіл хі-квадрат?

Розподіл хі-квадрат – це розподіл ймовірностей, символом якого є χ². Точніше, розподіл хі-квадрат — це сума квадратів k незалежних випадкових величин із нормальним розподілом.

Таким чином, розподіл хі-квадрат має k ступенів свободи. Отже, розподіл Хі-квадрат має стільки ступенів свободи, скільки сума квадратів змінних із нормальним розподілом, які він представляє.

$\displaystyle X\sim\chi^2_k \ \color{orange}\bm{\longrightarrow}\color{black}\ \begin{array}{l}\text{Distribuci\'on chi-cuadrado}\\[2ex]\text{con k grados de libertad}\end{array}$

Розподіл хі-квадрат також відомий як розподіл Пірсона .

Слід зазначити, що розподіл хі-квадрат є окремим випадком гамма-розподілу.

Розподіл хі-квадрат широко використовується в статистичних висновках, наприклад, для перевірки гіпотез і довірчих інтервалів. Нижче ми побачимо застосування цього типу розподілу ймовірностей.

Графік розподілу хі-квадрат

Коли ми побачимо визначення розподілу хі-квадрат, ми побачимо кілька прикладів цього типу розподілу, представлених графічно. Тож нижче ви можете побачити, як змінюється ймовірнісний графік розподілу хі-квадрат залежно від ступенів свободи.

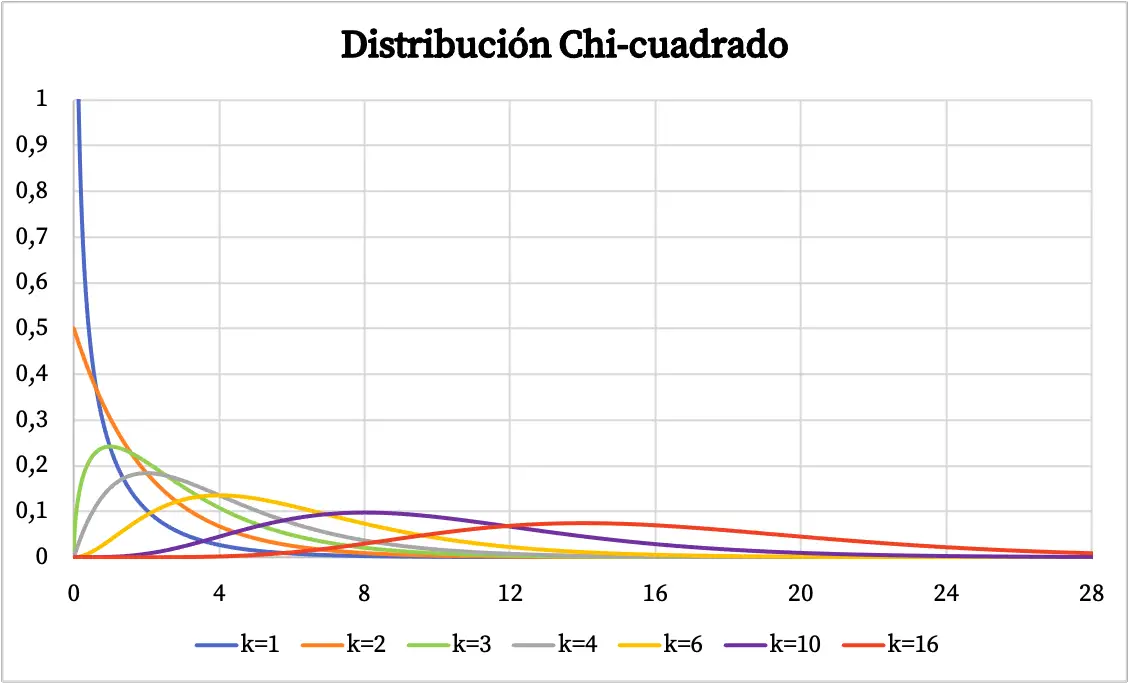
Функцію щільності розподілу хі-квадрат зображено на графіку вище. З іншого боку, графік кумулятивної функції розподілу ймовірностей хі-квадрат має такий вигляд:

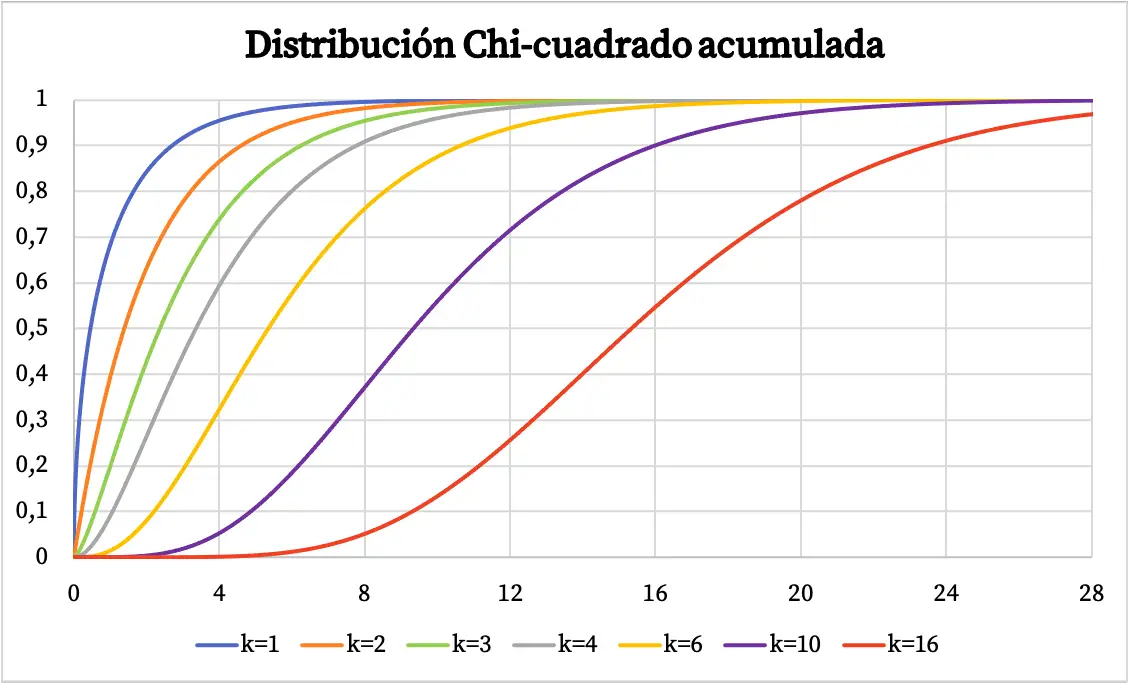
графік кумулятивного розподілу хі-квадрат

➤ Див. Таблицю розподілу хі-квадрат

Характеристика розподілу хі-квадрат

У цьому розділі ми побачимо найважливіші властивості розподілу хі-квадрат, пов’язані з теорією ймовірностей і статистикою.

Середнє значення розподілу хі-квадрат дорівнює його ступеням свободи.

$\begin{array}{c}X\sim\chi^2_k\\[2ex] E[X]=k\end{array}$

Дисперсія розподілу хі-квадрат дорівнює подвоєним ступеням свободи розподілу.

$\begin{array}{c}X\sim\chi^2_k\\[2ex] Var(X)=2\cdot k\end{array}$

Режим розподілу хі-квадрат на дві одиниці менший за його ступені свободи, якщо розподіл має більше ніж один ступінь свободи.

$Mo=k-2 \qquad \text{si } k\geq 2$

Функція щільності розподілу хі-квадрат дорівнює нулю, якщо x=0. Однак для значень x більше 0 функція щільності розподілу хі-квадрат визначається такою формулою:

$\displaystyle P[X=x]= \frac{(1/2)^{k/2}}{\Gamma(k/2)} x^{k/2 - 1} e^{-x/2}$

Кумулятивна функція розподілу хі-квадрат визначається такою формулою:

$\displaystyle P[X\leq x]=\frac{\gamma(k/2,x/2)}{\Gamma(k/2)}$

Коефіцієнт асиметрії розподілу хі-квадрат є квадратним коренем із частки восьми, поділеної на кількість ступенів свободи розподілу.

$\displaystyle A=\sqrt{\frac{8}{k}}$

Ексцес розподілу хі-квадрат обчислюється за таким виразом:

$C=3+\cfrac{12}{k}$

Завдяки центральній граничній теоремі розподіл хі-квадрат можна апроксимувати нормальним розподілом, якщо k достатньо велике.

$\displaystyle\lim_{k \to \infty} \frac{\chi^2_k (x)}{ k } = N_{\left(1,\sqrt{2/k}\right)} (x)$

Застосування розподілу хі-квадрат

Розподіл хі-квадрат має багато різних застосувань у статистиці. Насправді існує навіть тест хі-квадрат, який використовується для перевірки незалежності між змінними та відповідності теоретичному розподілу. Наприклад, критерій хі-квадрат можна використовувати, щоб визначити, чи відповідають дані вибірки розподілу Пуассона.

У лінійному регресійному аналізі розподіл хі-квадрат також використовується для оцінки середнього значення нормально розподіленої сукупності та для оцінки нахилу лінії дослідження лінійної регресії.

Нарешті, розподіл хі-квадрат також бере участь в дисперсійному аналізі через його зв’язок із розподілом F Снедекора.

Про автора

Редакція

Привіт, я Бенджамін, професор статистики на пенсії, який став викладачем статистики. Маючи великий досвід і знання в галузі статистики, я готовий поділитися своїми знаннями, щоб розширити можливості студентів через Statorials. Дізнайтеся більше