Симетричний розподіл: визначення + приклади

У статистиці симетричний розподіл — це розподіл, у якому ліва і права частини дзеркально відображають одна одну.

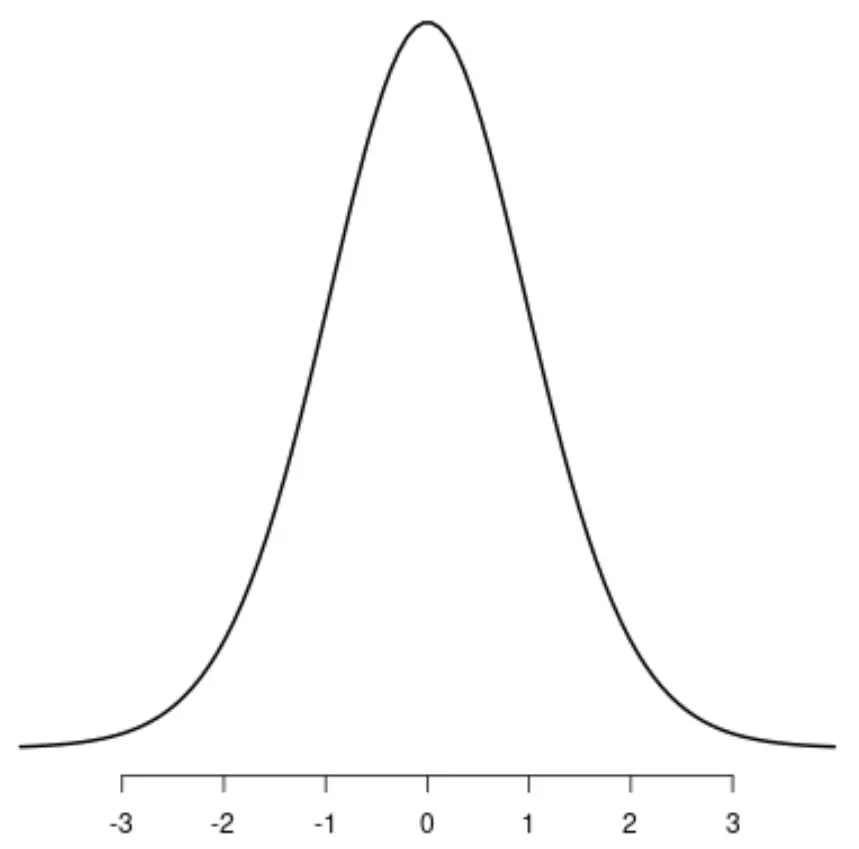
Найвідомішим симетричним розподілом є нормальний розподіл , який має чітку форму дзвона.

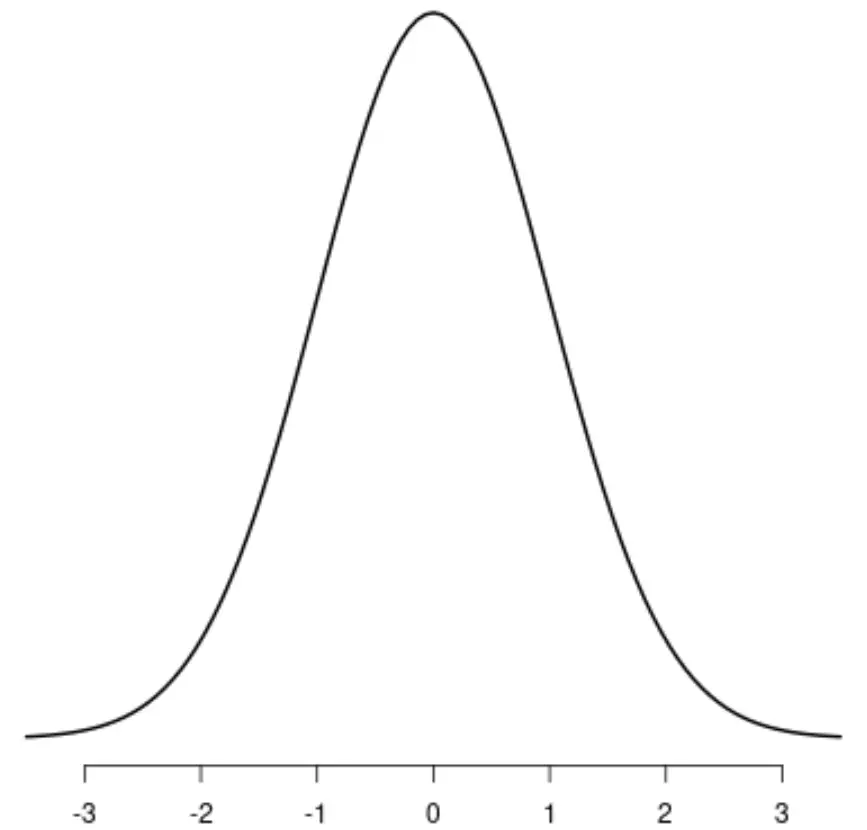
Якщо провести лінію по центру розподілу, ліва і права сторони розподілу будуть ідеально віддзеркалювати одна одну:

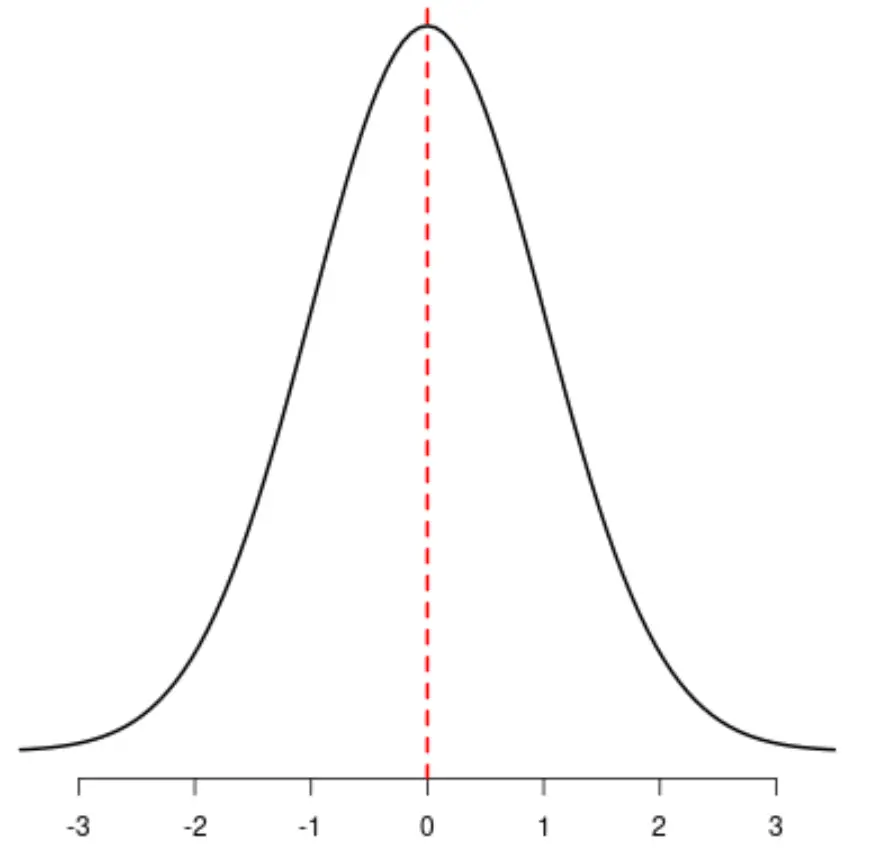
У статистиці асиметрія — це спосіб опису симетрії розподілу. Це значення може бути негативним, нульовим або позитивним.

Для симетричних розподілів асиметрія дорівнює нулю.

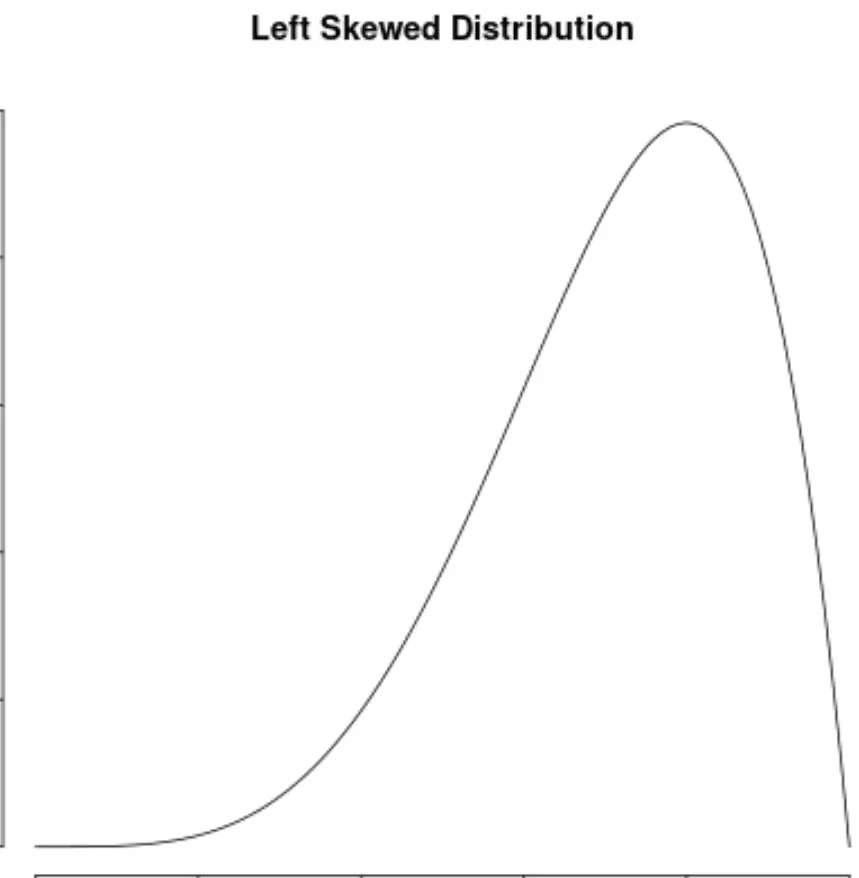
Це контрастує з лівосторонніми розподілами, які мають від’ємну асиметрію:

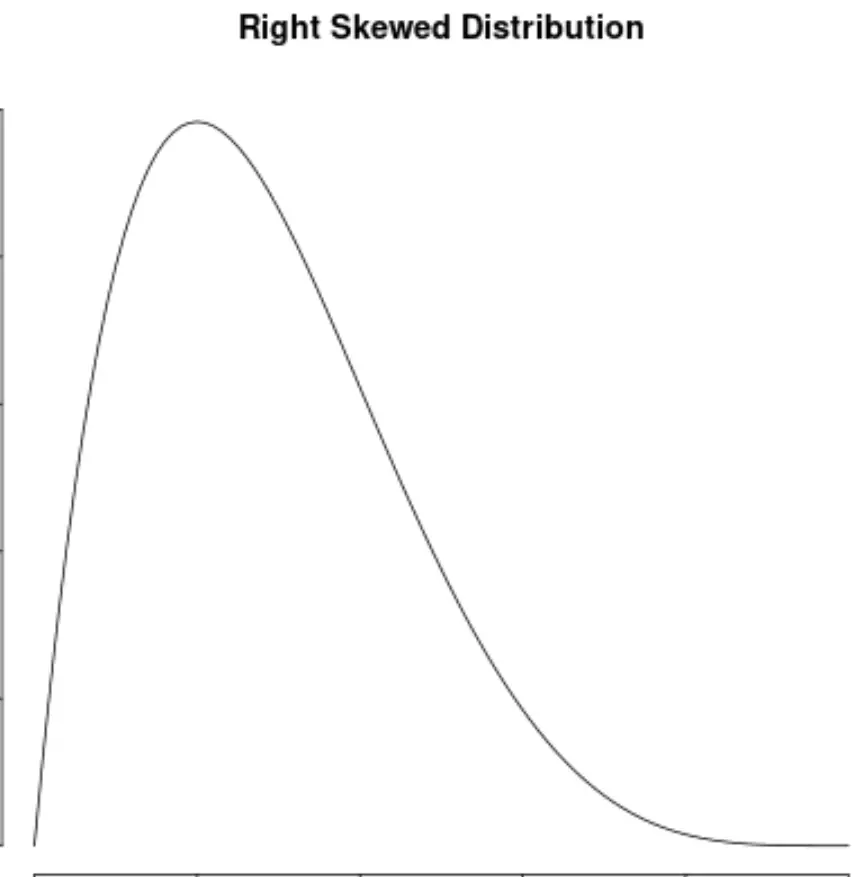
Це також контрастує з розподілами з правим викривленням, які мають позитивну зміщення:

Властивості симетричних розподілів

У симетричному розподілі середнє, медіана та мода рівні.

Запам’ятайте наступні визначення для кожного:

• Середнє: середнє значення.
• Медіана: середнє значення.
• Режим: значення, яке з’являється найчастіше.

У симетричному розподілі кожне з цих значень дорівнює іншому.

У кожному з прикладів досі ми використовували унімодальні розподіли як приклади – розподіли лише з одним «піком». Однак розподіл також може бути бімодальним і симетричним.

Бімодальний розподіл — це розподіл, який має два піки.

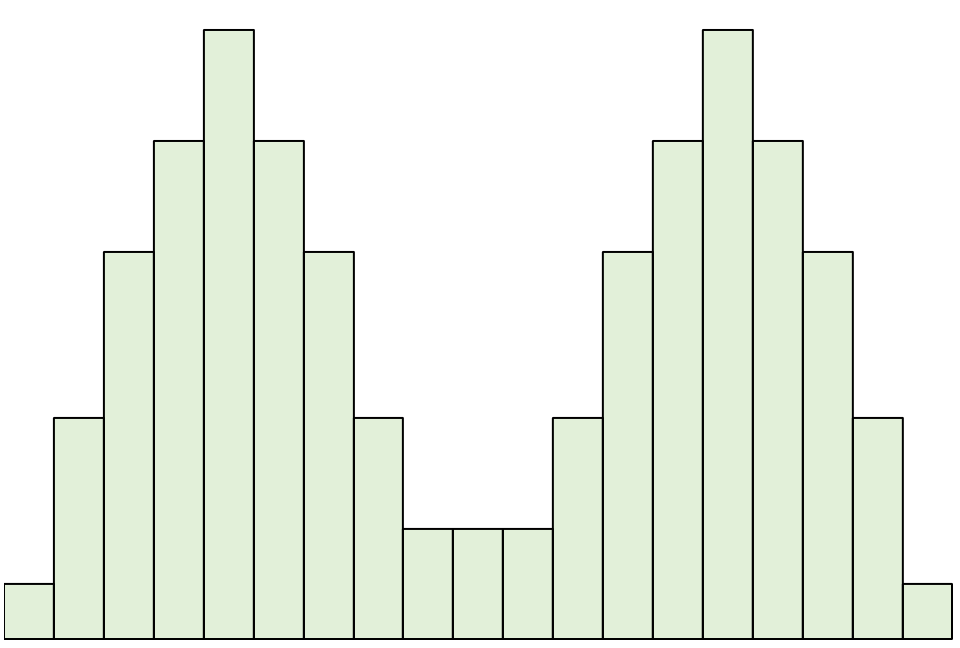
Зауважте, що якщо ми проведемо лінію вниз по центру цього розподілу, ліва і права сторони все одно будуть дзеркальними.

Для цих розподілів середнє та медіана рівні. Однак мода лежить в обох вершинах.

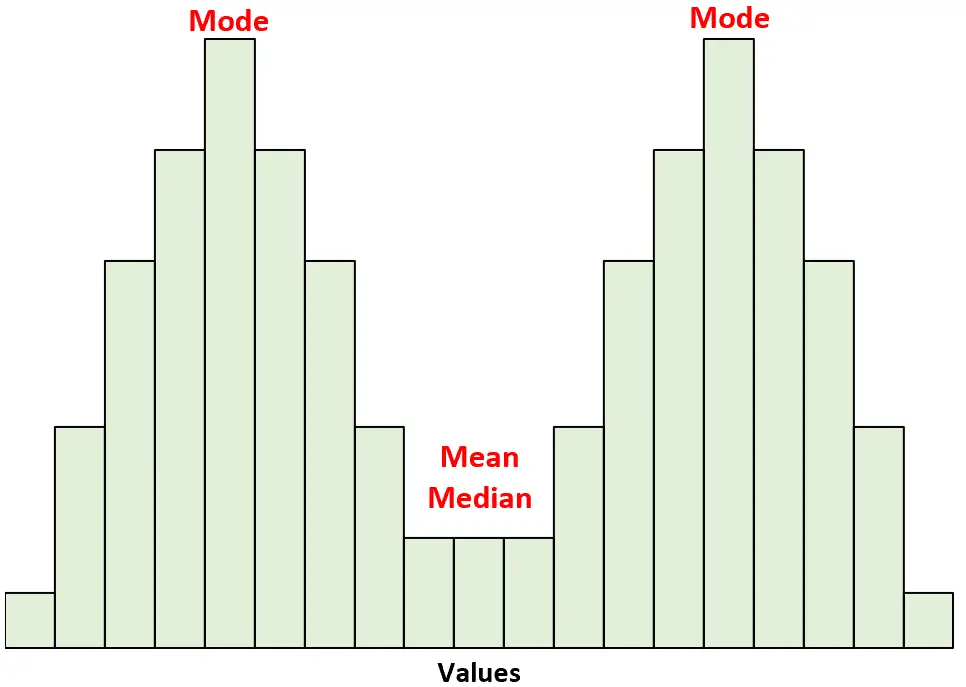
Інші приклади симетричних розподілів

Крім нормального розподілу симетричними є також такі розподіли:

Розподіл t

Рівномірний розподіл

Розподіл Коші

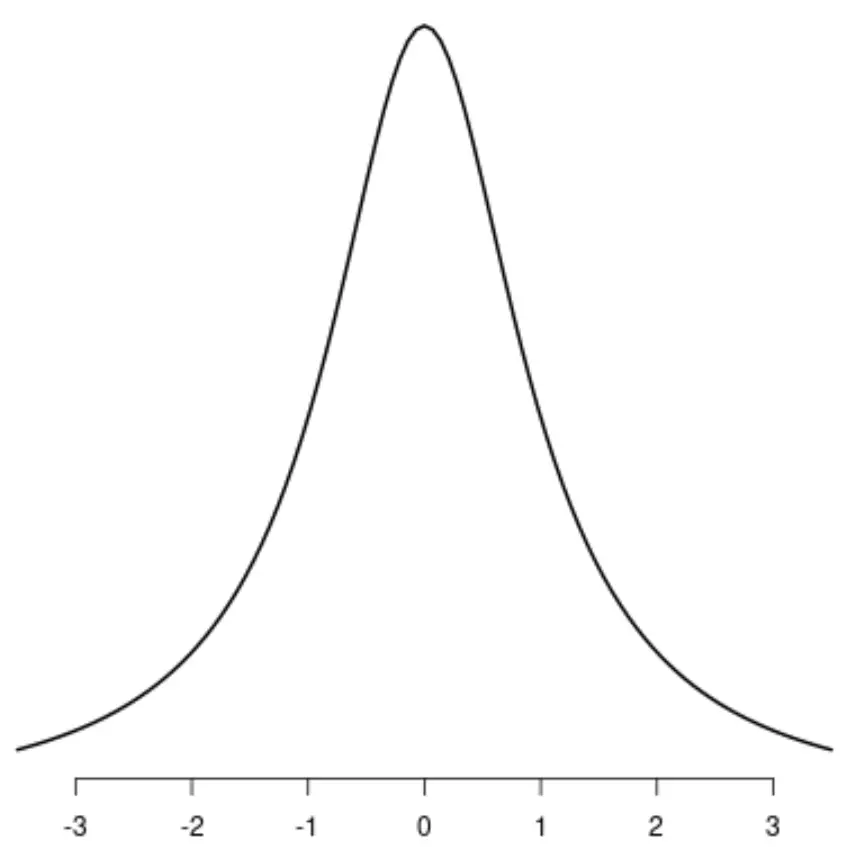
Якщо провести лінію по центру одного з цих розподілів, ліва і права сторони кожного розподілу будуть ідеально відображати один одного.

Симетричні розподіли та центральна гранична теорема

Однією з найважливіших теорем у всій статистиці є центральна гранична теорема, яка стверджує, що вибірковий розподіл вибіркового середнього є приблизно нормальним, якщо розмір вибірки достатньо великий, навіть якщо розподіл сукупності не є нормальним .

Щоб застосувати центральну граничну теорему, розмір вибірки має бути достатньо великим. Виявляється, скільки саме людей є «достатньо великими» залежить від основної форми розподілу населення.

Особливо:

• Якщо розподіл популяції симетричний, іноді достатньо лише 15 розмірів вибірки.
• Якщо розподіл популяції спотворений, зазвичай необхідна вибірка щонайменше з 30 осіб.
• Якщо розподіл популяції надзвичайно спотворений, може знадобитися вибірка з 40 або більше осіб.

Отже, перевага симетричних розподілів полягає в тому, що нам потрібні менші розміри вибірки для застосування центральної граничної теореми під час обчислення довірчих інтервалів або виконання перевірки гіпотез .

Додаткові ресурси

Вступ до центральної граничної теореми
Що таке бімодальний розподіл?
Посібник із лівих і правих викривлених розподілів