Скоригований коефіцієнт шансів: визначення + приклади
У статистиці співвідношення шансів показує нам співвідношення між ймовірністю події в групі лікування та ймовірністю події в контрольній групі.
Співвідношення шансів найчастіше з’являються в логістичній регресії , яка є методом, який ми використовуємо для підгонки регресійної моделі, яка має одну або кілька змінних предиктора та двійкову змінну відповіді.
Скоригований коефіцієнт шансів – це коефіцієнт шансів, скоригований для інших змінних предиктора в моделі.
Це особливо корисно, оскільки допомагає нам зрозуміти, як прогностична змінна впливає на шанси настання події після коригування впливу інших прогностичних змінних.
Наступний приклад ілюструє різницю між коефіцієнтом шансів і скоригованим коефіцієнтом шансів.
Приклад: Розрахунок скоригованих коефіцієнтів шансів
Припустимо, ми хочемо зрозуміти, чи впливає вік матері на ймовірність народження дитини з низькою вагою.
Щоб дослідити це, ми можемо виконати логістичну регресію, використовуючи вік як прогностичну змінну та низьку вагу при народженні (так чи ні) як змінну відповіді .
Припустімо, ми збираємо дані про 300 матерів і підбираємо модель логістичної регресії. Ось результати:
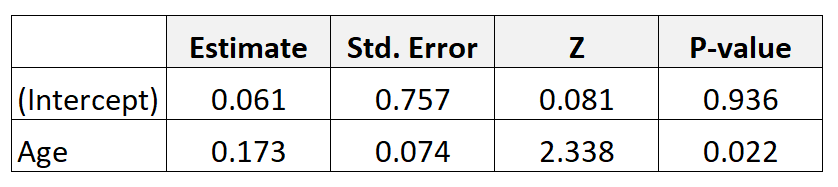
Щоб отримати відношення шансів для віку, просто підведіть до степеня оцінку коефіцієнта з таблиці: e 0,173 = 1,189 .
Це говорить нам про те, що збільшення віку на один рік пов’язане зі збільшенням на 1189 шансів народження дитини з низькою вагою. Іншими словами, шанси народити дитину з малою вагою збільшуються на 18,9% з кожним додатковим річним збільшенням віку.
Це відношення шансів називається «грубим» відношенням шансів або «нескоригованим» відношенням шансів, оскільки воно не було скориговано для інших змінних предиктора в моделі, оскільки це єдина змінна предиктора в моделі.
Але припустімо, що ми хочемо зрозуміти, чи впливають вік матері та її звичка до куріння на ймовірність народження дитини з низькою вагою.
Щоб дослідити це, ми можемо виконати логістичну регресію, використовуючи вік і куріння (так чи ні) як предикторні змінні та низьку вагу при народженні як змінну відповіді .
Припустімо, ми збираємо дані про 300 матерів і підбираємо модель логістичної регресії. Ось результати:
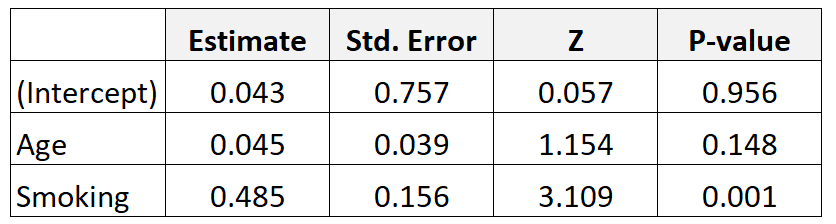
Ось як інтерпретувати результати:
Вік: Коефіцієнт шансів з поправкою на вік розраховується таким чином: e 0,045 = 1,046 . Це означає, що ймовірність народження дитини з низькою вагою при народженні зростає на 4,6% з кожним додатковим щорічним збільшенням віку, якщо припустити, що змінна куріння залишається постійною.
Наприклад, припустимо, що мати А і мати Б обидві курять. Якщо мати A на один рік старша за матір B, то ймовірність того, що мати A народить дитину з низькою вагою, в 1,046 рази перевищує ймовірність того, що мати B народить дитину з низькою вагою.
Куріння : скоригований коефіцієнт шансів для куріння розраховується таким чином: e,485 = 1,624 . Це означає, що ймовірність народження дитини з низькою вагою при народженні зростає на 62,4%, якщо мати курить (порівняно з тим, що не курить), припускаючи, що вікова змінна залишається постійною.
Наприклад, припустимо, що матері А і матері Б обом по 30 років. Якщо мати А курить під час вагітності, а мати Б не палить, то шанси матері А народити дитину з низькою вагою на 62,4% вищі, ніж шанси матері Б народити дитину з низькою вагою.
Зауважте, що відношення шансів із поправкою на вік нижче, ніж відношення шансів без поправок із попереднього прикладу. Це пояснюється тим, що коли інші змінні предиктора збільшують шанси появи змінної відповіді, скоригований коефіцієнт шансів для змінної предиктора, яка вже присутня в моделі, завжди зменшуватиметься.
Підсумок: співвідношення шансів проти скоригованого співвідношення шансів
Співвідношення шансів (іноді його називають «приблизним» співвідношенням шансів) корисно для того, щоб сказати нам, як зміни в змінній-прогнозі впливають на ймовірність появи змінної відповіді.
Скоригований коефіцієнт шансів корисний, щоб повідомити нам, як зміни в змінній предиктора впливають на ймовірність появи змінної відповіді після контролю інших змінних предиктора в моделі.
Додаткові ресурси
Вступ до логістичної регресії
Як виконати логістичну регресію в R
Як виконати логістичну регресію в Python